2.A The Basics of Fractions
Chad Flinn and Mark Overgaard
What exactly is a fraction, anyway? Have you ever dealt with fractions in either your schooling or your work? Well, a fraction is a part (or portion) of a whole.
Say you ordered a pizza and there were a total of 8 slices. You were hungry that day and you had 5 of them, therefore eating 5 out of the 8 slices. That can be represented as a fraction.

Defining a Fraction
Our story of fractions begins with Abigail, Hanna, and Naomi, who are electrical apprentices going through their schooling at the same time who hope to open a company together once they get their Red Seal Electrical Tickets.
We’ll start with a couple of definitions. Every fraction has two parts: the numerator and the denominator. Let’s take a look at a fraction to define each.
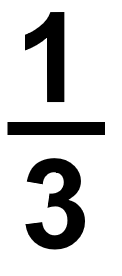
Numerator: The number above the line in a fraction. It indicates how many parts of the whole are being counted.
Denominator: The number below the line in a fraction. It indicates how many total parts are in the whole.
If Abigail, Hanna, and Naomi did end up owning a company, each would own ⅓ of that company. Each person represents 1 owner, and together, there are 3 owners in the whole company.
Here are a few more examples of fractions:
[latex]\LARGE\dfrac{1}{2}\ \dfrac{3}{8}\ \dfrac{5}{16}\ \dfrac{4}{9}\ \dfrac{7}{15}\ \dfrac{77}{145}[/latex]
Mixed Numbers and Improper Fractions
The examples above are all of typical fractions, but we don’t always see fractions in that form. There are two other styles of fractions that we deal with: mixed numbers and improper fractions.
Mixed numbers
Let’s say the three apprentices get together one night to talk about the future, and they order 2 pizzas, each with 8 pieces.

(I know the pizzas look exactly the same, but you’ll have to trust me on this one. One thing for sure is that each pizza has 8 slices, and someone has gone ahead and had a taste test of both pizzas.)
We need to break this down: we have a total of 2 pizzas, each with 8 slices. That makes for a total of 16 slices. If the apprentices eat 1 whole pizza, they will have eaten 8 out of 8 slices.
[latex]\LARGE\dfrac{8}{8}=1[/latex]
Now let’s say that one of the three of them has another slice from the second pizza. They will have now eaten 1 whole pizza plus 1 slice.
[latex]\LARGE1+\dfrac{1}{8}=1\dfrac{1}{8}\longleftarrow\text{Mixed number}[/latex]
This is what is known as a mixed number. A mixed number can be defined as the following:
Mixed number: A combination of a whole number and a fraction.
Next, we cover improper fractions.
Improper fractions
Improper fraction: A fraction in which the numerator is larger than the denominator.
What this means is that the number on the top of the fraction is larger than the number on the bottom. We’ll stick to our pizza example. Together, the apprentices have eaten a total of 9 slices. This accounts for 1 whole pizza plus 1 slice from the second pizza. Written as an improper fraction, the number of pizzas eaten would look like this:
[latex]\LARGE\dfrac{9}{8}[/latex]
Now, we want to change a mixed number into an improper fraction, and then do the reverse and take an improper fraction and change it back to a mixed number.
Example
Change the following mixed number into an improper fraction:
[latex]\LARGE1\dfrac{3}{4}[/latex]
Step 1: Change the whole number into a fraction, with the denominator being 4.
[latex]\LARGE1=\dfrac{4}{4}[/latex]
Step 2: Add the two fractions together. Now, we’ll have to jump ahead a little here, as we haven’t covered adding fractions yet. I’ll give you the cheap and easy version here. As long as the denominators are the same, we are all good. When adding fractions, we simply keep the denominators the same and add the numerators. (We’ll go through adding fractions thoroughly in the next chapter.)
[latex]\LARGE\dfrac{4}{4}+\dfrac{3}{4}=\dfrac{7}{4}[/latex]
So:
[latex]\LARGE1\dfrac{3}{4}=\dfrac{7}{4}[/latex]
Another way to find your answer would be as follows:
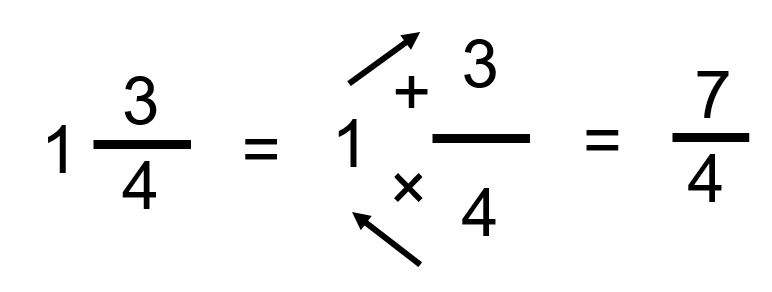
That may look a little confusing, but follow me through it. With the mixed number 1 ¾, take the 4 and multiply it by the 1. Then add 3, and you end up with 7. It’s the same answer — just a different way of getting there.
Try going from a mixed number to an improper fraction by yourself.
Practice Question A
Change the following into an improper fraction. Check the video answer to see how you did.
[latex]\LARGE3\dfrac{3}{8}[/latex]
All right: hopefully, you’ve got the mixed-number-to-improper-fraction calculation down. But what about the reverse? We should go through an example of that as well, and then give you a chance to work through one yourself.
Example
Change the following improper fraction into a mixed number:
[latex]\LARGE\dfrac{27}{6}[/latex]
Step 1: Find out how many times 6 goes into 27. We can do this using long division. The good news here is that we already went through long division in the first chapter. If you need to review it, take a look back to see how it’s done (see Dividing Whole Numbers).
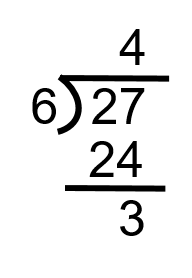
What we end up with is 6 going into 27 four times with 3 left over. So our mixed number becomes:
[latex]\LARGE4\dfrac{3}{6}[/latex]
Try another practice question.
Practice Question B
Change the following improper fraction into a mixed number. Check out the video answer to see how you did.
[latex]\LARGE\dfrac{17}{3}[/latex]
Reducing Fractions
Before we move on to adding and subtracting fractions, we should touch on another concept known as reducing fractions. Reducing is what we do when we want to make a smaller version of a fraction that still has the same mathematical value as the original.
Back to our pizza. Once again, we have 8 slices per pizza. Now, say we eat 4 of those slices. We have eaten:

If someone asked you how much pizza you had, how would you answer? Would you say, “I had 4 out of a possible 8 slices,” or would you say, “I ate half the pizza”? I think we’d all agree that we would just say that we ate half the pizza, as 4 pieces would amount to half the pizza. If we were to write half as a fraction, it would look like this:
[latex]\LARGE\dfrac{1}{2}[/latex]
We could then conclude that the two fractions represent the same thing mathematically, and they are just two different ways to represent the same thing. You could look at it this way: I cut two pieces of wood. One is 12 inches in length, and the other is 1 foot in length. They are the same length — their lengths are just expressed in different ways. So in the end, we end up with this:
[latex]\LARGE\dfrac{4}{8}=\dfrac{1}{2}[/latex]
What we’ve done is reduced the fraction from 4 over 8 to 1 over 2 without changing the actual value represented. How this was done mathematically is we took the original numerator of 4 and divided it by 4. What is done to one part of the fraction must also be done to the other, so we also divided the denominator of 8 by 4, resulting in a fraction of 1 over 2.
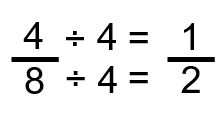
Doing the same thing to both the numerator and the denominator guarantees that the original fraction and the final fraction are equal in value.
We reduce fractions when we can evenly divide the same number into both the numerator and the denominator. In our example, 4 can be divided into both. Note that the number 2 can also be divided into both the numerator and the denominator. If we divided both by 2, we would get:
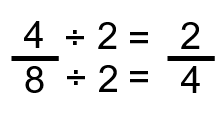
Although this still works mathematically, we often want to get a fraction into its lowest terms, meaning to a point where it can no longer be reduced. The fraction 2 over 4 could be reduced even further to 1 over 2, so there is further work we could do, if we chose to.
Example
Let’s go through the thought pattern when reducing fractions. Take the following fraction and reduce it to its lowest terms:
[latex]\LARGE\dfrac{8}{12}[/latex]
Step 1: What we want to do here is take a look at both the numerator and the denominator and determine if there is a number that can go into both of them. It might be easier if you write down numbers starting from 1 and then decide which numbers can go into both 8 and 12.
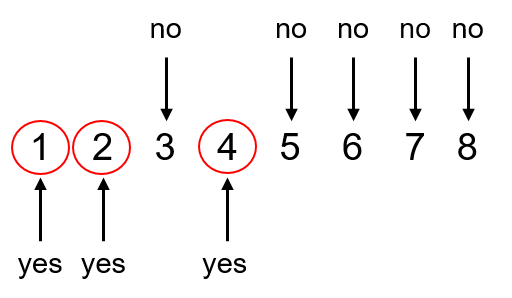
From this, we can conclude that the largest number that can go into both 8 and 12 is 4.
Step 2: Divide both the numerator and the denominator by 4.
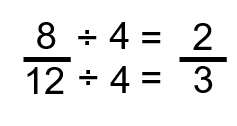
There you have it: the fraction has now been reduced to its lowest terms. Always take a look at the answer when you are done, just to make sure that there definitely isn’t another number that can go into the numerator and denominator, as this would mean the fraction could be reduced even further.
The example shown above is fairly straightforward. Once there are larger numbers involved, it is sometimes easier to work through the question in a couple of steps to slowly reduce the fraction. Take a look at the following example to see what I mean.
Example
Reduce the following fraction into its lowest terms:
[latex]\LARGE\dfrac{24}{168}[/latex]
Step 1: Determine if there is a number that can go into both the numerator and the denominator. If there is more than one number, then use the larger number.
This is a bit tougher than the first question, as the numbers are a lot larger and harder to work with. Going back to our times tables, we can see that 6, 8, and 12 all go into 24. We could also say that 24 goes into 24. But what about 168? What goes into that?
One thing we know for sure is that 2 goes into both, so why don’t we start by taking each part of the fraction and dividing it by 2. If you have trouble dividing 168 by 2 in your head, go ahead and use your calculator.
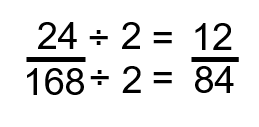
Step 2: Determine if the fraction can be reduced any further. We can see that, once again, we can divide both numbers by 2.
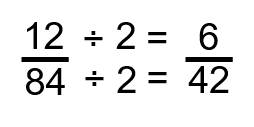
Step 3: Repeat step 2 and determine if the fraction can be reduced any further. What we note this time is that 6 can go into both 6 and 42, so we divide both the numerator and the denominator by 6.
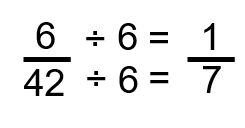
There you have it: we have reduced that large fraction into its lowest terms in just a few steps. I will admit that, if we had used a calculator for this whole procedure, we could have come up with the answer with less work, but that is not the point. Doing it the long way starts to train your brain in the relationships between numbers. As you get more familiar with numbers, you will be able to pick apart patterns and understand the relationships formed in math. Although it might be a little more time-consuming in the beginning, the payoff as time goes by is great.
Practice Questions
Try a couple questions for yourself and check the video answers to see how you did.
Reduce the following fractions into their lowest terms.
Question 1
[latex]\LARGE\dfrac{15}{18}[/latex]
Question 2
[latex]\LARGE\dfrac{24}{36}[/latex]

