3 Decimals & Percentages

Decimals

Much of the work done in health care involves the use of decimal numbers. Many instruments that are used give decimal readouts as you monitor patients. Medication dosages measured in milligrams, micrograms, or millilitres can often be given in decimal form. Updating patient records as well as billing and bookkeeping also requires the use of decimals. Therefore, it is important to be comfortable with calculations using decimals.

Place Value

Much like fractions, decimals represent a part of a whole. However, decimal fractions have denominators of [latex]10[/latex], [latex]100[/latex], [latex]1000[/latex], etc.

Refer to the following figure to review the place value of each digit in the decimal number: [latex]153.2785[/latex]

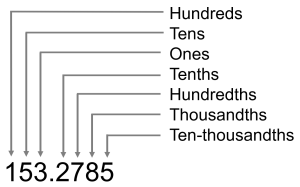
The whole number is found to the left of the decimal point and the fractional part of the number is found to the right of the decimal point. In the number shown above, [latex]153[/latex] is the whole number part of the decimal number, and [latex]2785[/latex] ten-thousandths is the fractional part of the decimal number.

If a decimal number is les than [latex]1[/latex], then a [latex]0[/latex] is used in the ones place in front of the decimal to reinforce the fact that the number is a proper fraction. For example [latex]0.3[/latex] = [latex]\frac3{10}[/latex] .

Understanding place value proves useful when comparing decimal numbers to determine which number is larger or smaller. For example when comparing [latex]0.074[/latex] and [latex]0.15[/latex], without considering place value, 74 may appear to be larger than 15.

To compare decimal numbers, make sure that each number has the same number of decimal places. As 0.074 has three decimal places, 0.15 can also be written as 0.150 so that a clear comparison can be made. We can now clearly state that 74 is smaller than 150.

[latex]\displaystyle 0.074<0.15[/latex].

Rounding Decimals

Understanding place value is integral to successfully rounding a decimal number. When working with decimals in health care, it is often necessary to round numbers to make them more manageable. Whether you round to a whole number, tenths place, hundredths place, or thousandths place will depend on the requirements of the problem and the precision needed.

Caution: Be mindful not to round in the process of problem solving. Rounding should only be done when a find answer has been found.

To round a number off, you always look at the number to the right of the digit being rounded. If that number is [latex]5[/latex] or higher, you add one to your digit; this is called rounding up. If that number is [latex]4[/latex] or less, you leave your digit alone; this is called rounding down.

1. Example: If you are rounding [latex]8.365[/latex] to two decimals (hundredths), you need to examine the number in the third decimal place (the one to the right). It is a [latex]5[/latex], so you add one to the second digit and the number becomes [latex]8.37[/latex].
2. Example: Let’s round [latex]3.6543[/latex] to the third decimal place (thousandths). Therefore, you look at the fourth decimal position, which is a [latex]3[/latex]. As the rule says, you would leave the digit alone and the number becomes [latex]3.654[/latex]

Nonterminating Decimals

What happens when you perform a calculation and the decimal doesn’t terminate?

1. 1. You need to assess if there is a clear pattern in the decimals:
      1. The Nonterminating Decimal without a Pattern:
         For example, [latex]\frac6{17}=0.352941176[/latex] with no apparent ending decimal and no clear pattern to the decimals.
      2. The Nonterminating Decimal with a Pattern:
         For example, [latex]\frac2{11}=0.18181818[/latex] endlessly. You can see that the numbers [latex]1[/latex] and [latex]8[/latex] repeat. A shorthand way of expressing this is to place a horizontal line above the digits that repeat.
         Thus, you can rewrite [latex]0.18181818[/latex] as [latex]0.\overline{18}[/latex].

• 2. You need to know if the number represents an interim or final solution to a problem

Interim Solution

You must carry forward all of the decimals in your calculations, as the number should not be rounded until you arrive at a final answer. If you are completing the question by hand, write out as many decimals as possible; to save space and time, you can use the shorthand horizontal bar for repeating decimals. If you are completing the question by calculator, store the entire number in a memory cell.

Final Solution

To round this number off, an industry protocol or other clear instruction must apply (such as the use of significant figures). If these do not exist, then you would make an arbitrary rounding choice, subject to the condition that you must maintain enough precision to allow for reasonable interpretation of the information.

Significant Figures (sig figs)

Significant figures (or significant digits) play a substantial role in the accuracy of health care measurements, such as laboratory tests, medication dosages, and vital signs.

While exact numbers are a counted quantity with no uncertainty (such as: 366 days in a leap year), approximate numbers are measured quantities and have a degree of uncertainty depending on the measuring device. For example: [latex]1.485\text{cm} \pm 0.005\text{cm}[/latex] on a device calibrated to millimeters.

All digits written to express an approximate numbers are significant except certain zeros.

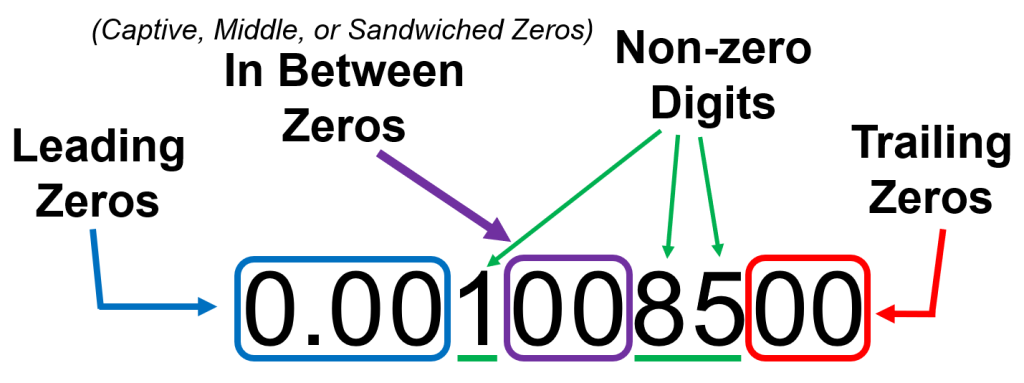
Leading zeros and trailing zeros to the left of the decimal in a whole number are NOT significant.

Trailing zeros to the right of the decimal and captive zeros (found in between sig figs) are significant.

Take note that accuracy refers to the number of significant figures in a measured value.

Example: 543 200 has an accuracy of 4 significant figures.

Whereas, precision refers to the placement of the significant figure furthest to the right. This is also known as decimal position or decimal place.

Example: 543 200 has a precision to the hundreds place.

Precision & Accuracy within Calculations

Calculations that involve addition or subtraction should state the final result to the precision of the least precise given number.

Examples:

[latex]14.2mg + 17.35mg - 3.221mg = 28.329 = 28.3mg[/latex]
(note that the final place value of the lease precise number is the tenths)

[latex]14.200mg + 17.359mg + 3.221mg = 34.78 = 34.780mg[/latex]
(as all numbers have a final place value of thousandths, so must the final response)

Calculations that involve multiplication or division should state the final result to the accuracy of the least accurate given number.

Examples:

[latex]14.2 \text{mg} \times 17.35mg \div 3.221mg = 76.4888668 = 76.5mg[/latex]
(note that the least accurate number has three significant figures)

[latex]75.55m \times 3.25m = 245.5375 = 246m^2[/latex]
(note that the least accurate number also has three significant figures)

Operations with Decimals

Although calculators may often be used to save time, understanding how to perform operations with decimal numbers without a calculator further demonstrates your understanding of the concept.

Addition & Subtraction

Adding and subtracting decimal numbers is not complicated. The method uses similar operational rules as when adding and subtracting with whole numbers. It is recommended to write the operation vertically to make the problem easier.

The essential component is to line up the decimal points before you begin your calculations. Recall that all whole numbers have an invisible decimal point located to the right, at the end, of the whole number

Example A

[latex]5 + 8.4 + 0.017 + 2.18 = [/latex]

[latex]\begin{align*}&5 \\ &8.4 \\ &0.017 \\ +&\underline{2.18} \\ =1&5.597 \end{align*}[/latex]

Example B

[latex]3.57 - 1.002 =[/latex]

[latex]\begin{align*} -3.570& \text{(note the extra zero used to facilitate the subtraction)}\\ \underline{-1.002}& \\ = -2.568& \end{align*}[/latex]

Multiplication

The process to multiply decimal numbers is quite straightforward, as you simply ignore the decimal points and multiply the numbers as you would when multiplying whole numbers. There is no need to line up the decimal points when writing out your work.

The key component is to ensure that your final answer has the total number of spots after dots. To do this, count the total number of decimal places within the numbers being multiplied together. This will inform how many decimal places will be needed when stating your response.

[latex]\begin{align*}-3.570& \text{(note the extra zero used to facilitate the subtraction)}\\ \underline{ -1.002}&  \\ = -2.568& \end{align*}[/latex]

Example
[latex]\begin{align*}&3.451 \leftarrow \text{ three decimal places} \\ \times &\underline{6.2} \leftarrow \text{ one decimal place} \\ &6902 \\ &\underline{207060}  \\ = 2&1.3962  \leftarrow \text{ total of four decimal places}\end{align*}[/latex]

Division

Long division of decimal numbers is a little more involved. The first essential component is that your outside number (divisor) must be a whole number. This can be accomplished through making the decimal invisible by moving the decimal point the appropriate number of places to the right so that it is at the end of the number. To ensure that your original numbers remain equivalent, you must also move the decimal point in your inside number (dividend) the same number of places to the right.

From here, you perform the long division using the same steps as you would with whole numbers. The final key component is to bring the decimal point (in its new position) up in the answer.

Example: [latex]1.7225 \div 3.25[/latex]

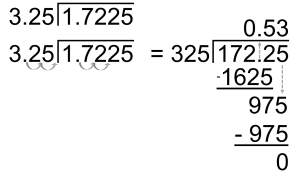
The answer to [latex]1.7225 \div 3.25[/latex] is [latex]0.53[/latex].

Converting Decimals to Fractions

As previously mentioned, decimal numbers can also be referred to as decimal fractions where the denominators are multiples of ten. To convert a decimal to a fraction, use the number that appears to the right of the decimal as the numerator and the denominator will be the numerical value of the final place value.

For example, [latex]0.013[/latex] (or thirteen thousandths) can be represented by the fraction [latex]\frac{13}{1000}[/latex].

In the case of a number larger than [latex]1[/latex], such as [latex]4.3[/latex] (four and three tenths), the fractional notation would be represented by the mixed number [latex]4\frac3{10}[/latex].

Converting Fractions to Decimals

Although fractions are common, many people have trouble interpreting them. For example, in comparing [latex]\frac{27}{37}[/latex] to [latex]\frac{57}{73}[/latex], which is the larger number? The solution is not immediately apparent. Therefore, fractions are converted into decimals by performing the division to make them easier to understand and compare.

Convert fractions into decimals based on the fraction types and fraction rules

Proper and Improper Fractions

Resolve the division. For example, [latex]\frac34[/latex] is the same as [latex]3\div4=0.75[/latex]. As well:

[latex]\begin{eqnarray*}&\;&\frac54\\[1ex]&=&5\div4\\&=&1.25\end{eqnarray*}[/latex]

Mixed Numbers

The decimal number and the fraction are joined by a hidden addition symbol. Therefore, to convert to a decimal you need to reinsert the addition symbol and apply BEDMAS:

[latex]\begin{eqnarray*}&\;&3\frac45\\[1ex]&=&3+4\div5\\&=&3+0.8\\&=&3.8\end{eqnarray*}[/latex]

Complex Fractions

The critical skill here is to reinsert all of the hidden symbols and then apply the rules of BEDMAS:

[latex]\begin{eqnarray*}&\;&2\frac{\displaystyle\frac{11}4}{1{\displaystyle\frac14}}\\[1ex]&=&\;2+\left[\frac{(11\div4)}{(1+1\div4)}\right]\\[1ex]&=&2+\left[\frac{(11\div4)}{(1+0.25)}\right]\\[1ex]&=&2+\left[\frac{2.75}{1.25}\right]\\[1ex]&=&2+2.2\\&=&4.2\end{eqnarray*}[/latex]

Practice converting these fractions and rounding the decimals.

Converting between Decimals and Percentages

The meaning of percent translates to per hundred, and it is denoted using the symbol: [latex]%[/latex]. Percentages also represent a part of a whole, where the total is always out of 100. Decimal numbers can be easily converted to percentages by simply multiplying the decimal number by 100. Alternatively, you can move the decimal point to the right by two places.

Examples: The decimal number: [latex]0.17[/latex] is identical to the percentage [latex]17%[/latex].

The decimal number: [latex]0.4[/latex] is identical to the percentage [latex]40%[/latex].

Similarly, percentage notations can be converted to decimal numbers by dividing by 100 or moving the decimal point to the left by two places.

Examples: The percentage: [latex]7.5%[/latex] is identical to the decimal number[latex]0.075[/latex].

The percentage: [latex]3%[/latex] is identical to the decimal number[latex]0.03[/latex].
(recall the invisible decimal point at then end of a whole number)

To convert fractions to percentages, first change the fraction to a decimal by dividing the top number by the bottom number. Then convert the decimal to a percentage as shown above.

Percentages

A solid understanding of percentages will assist you in your profession as a health care worker. Percentages are found in many areas within the health field, including: finding the strength of medication, interpreting data from a patient’s chart, and preparing solutions with diluted stock supplies.

Recall that a percentage is a fraction that has a denominator of 100. This means that every percentage can be expressed as a fraction.

[latex]88\%[/latex] is the same as [latex]\frac{88}{100}[/latex]
This fraction can then be reduced to [latex]\frac{22}{25}[/latex]

Applications of Percentages

Medications are made in both pure form and diluted form. If the drug has no diluting agent, it is considered to be a pure drug. However, many drugs are in solution form and made by diluting some of the pure drug in a liquid. Recall that percentage is defined by parts per hundred. Therefore, the strength of the solution can be expressed as a percentage when the amount of pure drug (in solid or liquid form) is per 100 parts of solution.

If a pure drug is in solid form, 1% solution means 1g of pure drug in 100mL of solution. Alternatively, if a pure drug is in liquid form, 1% solution translates to 1mL of pure drug in 100mL of solution. As you will not always have volumes of 100mL, understanding how to covert a fraction to a percentage is necessary.

Part of Whole

When you are presented with a scenario where you are given a part of the total amount (whole), you can calculate the percentage using the following formula:

[latex]\Large\frac{part}{total}\;[/latex] x [latex]\;100\;=\;\%[/latex]

Example: Find the percentage strength (or concentration) of a medication containing 15mL of pure drug mixed with 40mL of water.
(Note that the total solution is 55mL, as it is the pure drug mixed with water)

[latex]\Large\frac{15}{55}\;[/latex] x [latex]\;100\;=\;27\%[/latex]

Percent of a number

It should be noted that when you are asked to find the fraction of a number or the percent of a number, the word of indicates a multiplication. This differs to what we just saw with ‘of’ used in part of a whole. When the meaning is ‘out of’, division is the operation used.

The most practical approach to finding the percent of a number is to first change the percentage to a decimal and then multiply it by the number provided.

Examples: Calculate the lowest annual salary for a nurse in Halifax, Nova Scotia if it is 52.9% of the average annual salary of $79,280.

[latex]0.529 \times 79,280 = $41,939.12[/latex]

Calculate the highest annual salary for a nurse in Halifax, Nova Scotia if it is 145.5% of the average annual salary of $79,280.

[latex]1.455 \times 79,280 = $115,352.40[/latex]

Percentage Increase and/or Decrease

When presented with data, there may be times when you want to calculate the percentage increase or decrease. This can be particularly useful when analyzing health care statistics.

To find the change in percentage, you must first find the difference between the two numbers (through subtraction). You would then take that difference and divide it by the original amount, as indicated by the following formulas.

[latex]\%\;\text{increase } = \frac{\text{amount of increase}}{\text{original amount}}[/latex]

[latex]\%\; \text{decrease } = \frac{\text{amount of decrease}}{\text{original amount}}[/latex]

Example: Determine the percentage increase of male registered nurses in Canada between 2010 and 2020 if there were 17,841 in 2010 and 26,854 in 2020.

[latex]\%\; \text{increase} = \Large\frac{9013}{17841}\normalsize = 50.5\%[/latex]

Chapter Credit

Chapter (including Case Studies) consists of original content.