22 pH & Concentrations
Learning Objectives
- Determine the concentration of Hydroxide ions in a solution
- Determine the Hydrogen ion concentration of an acid.
- Use Logarithms to calculate pH and pOH
- Calculate the pH and pOH of an ionic solution
- Calculate the Hydrogen concentration from pH
Ionic Solutions
Due to their opposite electrical charges, ions are attracted to each other in a compound. If ionically bonded molecules are dissolved in a solvent, they will dissociate because the ionic bonds are broken. Generally, there are three categories of ionic compounds: acids, bases, and salts.
When an acid is added to water, it releases hydrogen ions (H+) which will increase the concentration of hydrogen ions. An acidic solution contains more H+ ions than OH– ions.
This resulting acidic solution is said to have a pH lower than 7.
Example 1
Saliva or black coffee (weak acidic solutions) have a pH of 6 and 5 respectively.
Stomach acid (a strong acidic solution) has a pH of 1.
When a base is added to water, it releases hydroxide ions (OH–) which then decreases the concentration of hydrogen ions (H+). A basic or alkaline solution has more OH– ions than it does H+ ions. This resulting basic (or alkaline) solution is said to have a pH greater than 7.
Example 2
Ocean Seawater (a weak basic solution) has a pH of 8.
Bleach (a strong basic solution) can have a pH of 13.
In a neutral solution, such as an aqueous solution of sodium chloride (aka: brine or salt in water), the numbers of H+ and OH– ions are equal and therefore has a pH value of 7.
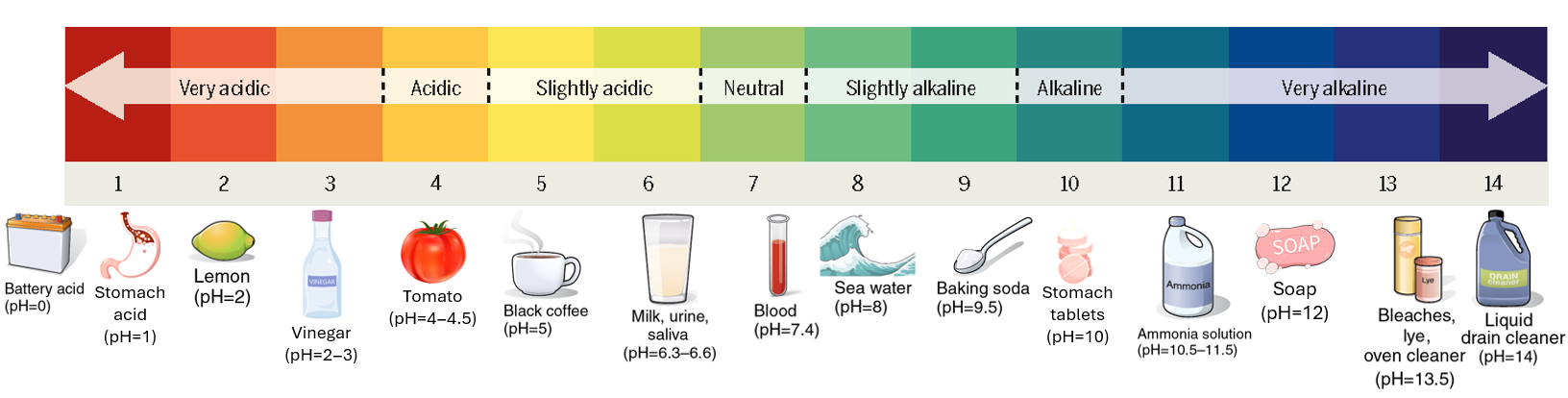
pH Readings
When you take a pH (Potential Hydrogen) reading you discover how many hydrogen ions are in the sample. The results fall on a scale of 0 to 14, with 0 being the most acidic and 14 being the most alkaline. Completely pure water will register in the middle at 7 and is considered neutral.
Alternatively, pOH (Power of Hydroxide ion) is a measure of the alkalinity of a solution. It is used to estimate the hydroxide ion (OH–) concentration in a solution, expressing the basicity of a solution.
The relationship between the pH and pOH is such that when we add the pH and the pOH for the same solution we get 14.
[latex]\text{pH} + \text{pOH} = 14[/latex]
Therefore, if sea water has a pH of 8, it will have a pOH of 6.
Sample Exercises 22.1
- Find the pOH of the following solutions.
a) Orange juice with a pH of 3
b) Laundry detergent with a pH of 9
c) Red wine with a pH of 4 - Find the pH for the following solutions.
a) a slightly acidic solution with a pOH of 9.6
b) a slightly alkaline solution with a pOH of 5.5
c) a very basic solution with a pOH of 1.8
Solutions
[latex]\text{pH} + \text{pOH} = 14[/latex]
[latex]\text{pOH} = 14 - \text{pH}[/latex]
or
[latex]\text{pH} = 14 - \text{pOH}[/latex]
Answers
1a) The pOH of orange juice is 11
b) The pOH of the laundry detergent is 5
c) The pOH of the red wine is 10
2a) The pH of the acidic solution is 4.4
b) The pH of the slightly alkaline solution is 8.5
c) The pH of the very basic solution is 12.2
Molarity and Normality.
Two of the ways to express the concentration of ion in a solution are molarity and normality.
The amount of substance dissolved in a solution is measured in moles per litre (mol/L) or M and is referred to as molarity.
In all water solutions (acid, base, or neutral), the molar concentration of the hydrogen ions [H+] multiplied by the molar concentration of the hydroxyl ions [OH–] will equal to [latex]0.00000000000001[/latex] or [latex]\times 10^{14}[/latex]
This relationship can be described by the formula:
[latex][H^{+}] × [OH^{-}] = 1 × 10^{-14}[/latex]
If the concentration of hydrogen ions in a particular solution is known, we can use this relationship to determine the concentration of hydroxide ions in the solution.
Sample Exercise 22.2
Find the concentration of hydroxide ions [OH–] in an aqueous solution that has a hydrogen concentration [H+] of 0.005 mol/L.
Solution
Since [H+] = 0.005, subsitute this value into the equation and solve.
[latex][H^{+}]× [OH^{-}] = 1 × 10^{-14}[/latex]
[latex]0.005 × [OH^{-}] = 1 × 10^{-14}[/latex]
Divide each side by 0.005 (or 5 × 10-3)
[latex]\frac{1×10^{-14}}{5×10^{-3}}[/latex]
[latex]= 0.2 × 10^{-11}[/latex]
Recall that the initial number of an answer in Scientific Notation must be at least 1 and smaller than 10.
[latex]= 2 × 10^{-12}[/latex]
Answer
The concentration of hydorxyl ions [OH–] is 2 × 10-12 mol/L
The concentrations of many acids is given in normality, a concentration unit that is based on a unit of mass called the equivalent weight, instead of the gram molecular weight used for molarity.
The hydrogen ion concentration [H+] in a given solution depends upon the percent of ionization that occurs in the solution. In strongly acidic or basic solution, the percent of ionization is usually known, and [H+] can be determined from the normality, N, using the following formula:
[latex][H^{+}] = \text {N ×} \% \text{ ionization}[/latex]
Strong acids, such as hydrochloric acid (HCl) and sulfuric acid (H2SO4) readily dissociate in water (100% ionization). Weak acids, such as acetic acid (CH3COOH) will only only slightly dissociate into a solution. We can assume this dissociation to be 1%.
Sample Exercises 22.3
a) What is the hydrogen ion concentration [H+] of a 0.3 N solution of H2SO4?
b) What is the hydrogen ion concentration of a 1.5 N solution of acetic acid?
Solutions
The molar concentration of hyrdrogen can be calculated as follows:
[latex][H^{+}] = \text {N ×} \% \text{ ionization}[/latex]
a)
[latex][H^{+}] = 0.3 N × 100\%[/latex]
[latex][H^{+}] = 0.3 × 1[/latex]
[latex][H^{+}] = 0.3[/latex]
b)
[latex][H^{+}] = 1.5 N × 1\%[/latex]
[latex][H^{+}] = 1.5 × 0.01[/latex]
[latex][H^{+}] = 0.015[/latex]
Answers
a) [H+] = 0.3 mol/L H+ in a 0.3 N solution of H2SO4.
b) [H+] = 0.015 mol/L H+ in a 1.5 N acetic acid solution.
Using Logarithms to Calculate pH and pOH
In 1909, when Swedish chemist S.P.L. Sorensen developed the pH system, he defined pH as the common logarithm of the reciprocal of the concentration of the hydrogen ions in a solution, measured in moles per litre .
[latex]\text{pH = log}\frac{1}{[H^{+}]}[/latex]
Take note that you may also encounter pH defined as:
[latex]\text{pH = - log}[H^{+}][/latex]
This formula is the equivalent to the one mentioned previously, and either can be used when determining the hydrogen ion concentration in a solution or solving for the pH given the concentration of hydrogen ions.
Sample Exercises 22.4
a) If the concentration of hydrogen ions in a solution is 0.0078 mol/L, the what is the corresponding pH of that solution?
b) If the pH of a solution is 8.3, then what is the concentration of hydrogen ions in moles per litre?
Solutions
a)
[latex]\text{pH = log}\frac{1}{[H^{+}]}[/latex]
[latex]\text{pH = log}\frac{1}{0.0078}[/latex]
[latex]\text{pH = log 128.2051282}[/latex]
[latex]\text{pH = 2.1079}[/latex]
or
[latex]\text{pH = - log}[H^{+}][/latex]
[latex]\text{pH = - log 0.0078}[/latex]
[latex]\text{pH = - (-2.1079)}[/latex]
[latex]\text{pH = 2.1079}[/latex]
b)
[latex]\text{pH = log}\frac{1}{[H^{+}]}[/latex]
[latex]\text{8.3 = log}\frac{1}{[H^{+}]}[/latex]
[latex]8.3 = \text{log}_{10} \frac{1}{[H^{+}]}[/latex]
change from logarithmic form to exponential form
[latex]10^{8.3} = \frac{1}{[H^{+}]}[/latex]
[latex][H^{+}] × 10^{8.3} = 1[/latex]
[latex][H^{+}] = \frac{1}{10^{8.3}}[/latex]
[latex][H^{+}] = 5.01 × 10^{-9}[/latex]
Answers
a) The pH of the solution is 2.1
b) [H+] = 5.01 x 10-9 mol/L
Similarly, pOH is defined as the common logarithm of the reciprocal of the concentration of the hydroxide ions in a solution, measured in moles per litre.
[latex]\text{pOH = log}\frac{1}{[OH^{-}]}[/latex]
Take note that you may also encounter pOH defined as:
[latex]\text{pOH = - log}[OH^{-}][/latex]
This formula is the equivalent to the previous, and either can be used when determining the hydroxide ion concentration in a solution or solving for the pOH given the concentration of hydrogen ions.
Sample Exercises 22.5
a) What is the pOH of a solution with a hydroxide ion concentration of [latex]6.1 \times 10^{-4} text{mol/L?}[/latex]
b) If the pOH of a solution is 9.1, then what is the hydroxide ions in moles per litre?
Solutions
a)
[latex]\text{pOH} = \text{log } \frac{1}{[OH^{-}]}[/latex]
[latex]\text{pOH} = \text{log } \frac{1}{6.1×10^{-4}}[/latex]
[latex]\text{pOH} = \text{log } \frac{1}{0.00061}[/latex]
[latex]\text{pOH} = \text{log } 1639.344262[/latex]
[latex]\text{pOH} = 3.21467[/latex]
or
[latex]\text{pOH}= - \text{log } 6.1\times 10^{-4}[/latex]
[latex]\text{pOH} = - \text{log } 0.00061[/latex]
[latex]\text{pOH} = - (-3.21467)[/latex]
[latex]\text{pOH} = 3.21467[/latex]
b)
[latex]\text{pOH} = \text{log } \frac{1}{[OH^{-}]}[/latex]
[latex]9.1 = \text{log } \frac{1}{[OH^{-}]}[/latex]
[latex]9.1 = \text{log }_{10} \frac{1}{[OH^{-}]}[/latex]
change from logarithmic form to exponential form
[latex]10^{9.1} = \frac{1}{[OH^{-}]}[/latex]
[latex][OH^{-}] × 10^{9.1} = 1[/latex]
[latex][OH^{-}] = \frac{1}{10^{9.1}}[/latex]
[latex][OH^{-}] = 7.94 × 10^{-10}[/latex]
Answers
a) The pOH of the solution is 3.2
b)[latex][OH^{-}] = 7.94 \times 10^{-10} \text{ mol/L}[/latex]
To calculate the the concentration of hyrdrogen ions in a solution from the pH number, the use of the antilogarithm function is required. Using this function will reverse the process used to calculate the pH number as observed in the following relationships.
[latex][H^{+}] = \text {antilog(-pH)} = 10^{\text{-pH}}[/latex]
[latex][OH^{-}] = \text {antilog(-pOH)} = 10^{\text{-pOH}}[/latex]
Take note that antilog can also be written as: [latex]\text {log}^{-1}[/latex]
Sample Exercise 22.6
An acid solution has a pH of 1.5. Find the hydrogen ion concentration of this solution.
Solutions
[latex][H^{+}] = \text {antilog(-pH)}[/latex]
[latex][H^{+}] = \text {antilog(-1.5)}[/latex]
recall that the antilog can be solved using the [10x] button on your calculator.
[latex][H^{+}] = 10^{-1.5}[/latex]
[latex][H^{+}] = 0.031622776[/latex]
Answer
The hydrogen ion concentration [H+] is 0.0316 mol/L.
Key Takeaways: Important Equations
- [latex][H+] \times [OH-] = 1 x 10^{-14}[/latex]
- [latex]pH + pOH = 14[/latex]
- [latex]pH = -log [H^{+}][/latex]
- [latex]pOH = -log [OH^{-}][/latex]
- [latex][H^{+}] = N \times \% \text{ ionization}[/latex]
- [latex][H^{+}] = \text{antilog} (-pH) = 10^{-pH}[/latex]
- [latex][OH^{-}] = \text{antilog} (-pOH) = 10^{-pOH}[/latex]
Case Study
Scenario A: pH of a Weak Acid Solution (Saliva)
Samantha works in a health clinic in Kentville, Nova Scotia, where she is asked to check the pH of a sample of saliva. The clinic uses saliva as part of routine checks for acidity levels in patients with oral health concerns. Samantha finds the pH to be 6.0.
Question: What is the molarity of the hydrogen ion concentration in the saliva sample?
SolutionSteps to Solve:
The formula for pH is:
[latex]\text{pH} = −\text{log}[H]^{+}[/latex]
Rearrange the formula to solve for [H+]:
[latex][H^{+}] = 10^{−pH}[/latex]
For saliva with a pH of 6.0:
[latex][H^{+}] = 10^{−6}[/latex]
So, the molarity of hydrogen ions in the saliva is [latex]1 × 10^{−6} mol/L.[/latex]
Chapter Credit
Chapter (including Case Studies) consists of original content.

