21 Logarithms
Learning Objectives
- Change from exponential form to logarithmic form and vice-versa
- Demonstrate an understanding of common log, natural log, and anti-log
- Evaluate logarithms
- Solve exponential equations using logarithms
logarithmic functions
In the health care industry, logarithms are used frequently in the chemistry lab. Measuring pH and pOH concentrations, plotting of standard cruves, determining rates of radioactive decay or bacterial growth, half-life calculations for radioactive tracers and elements, and population growth rates are all examples where logarithms are used.
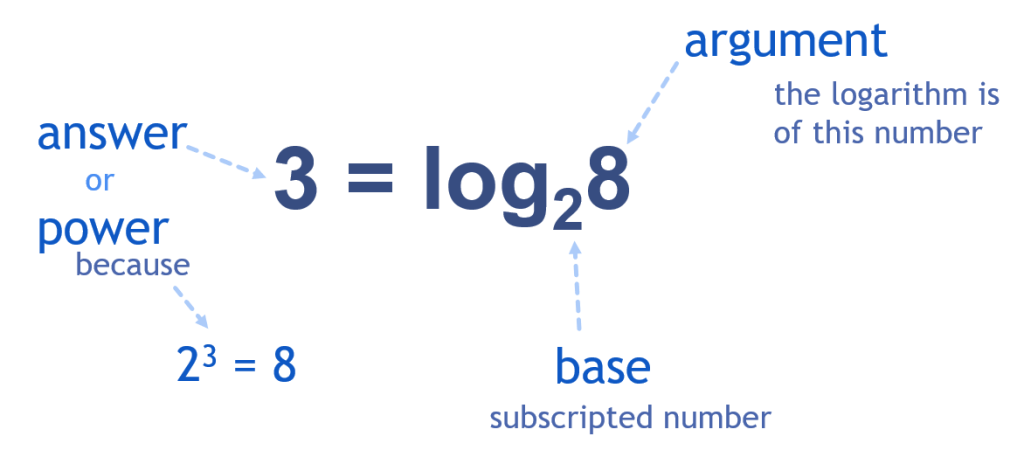
A logarithm is the exponent (or power) that a base must be raised to produce another value (argument). In working with equations or formulas that use logarithms, certain abbreviations are used. The word logarithm and the phrase logarithm of are abbreviated log.
Example
[latex]2^{3 } = 8[/latex]
Therefore, 3 is the logarithm of 8 to base 2.
You could also say: “Log base 2 of 8 is 3”.
Conversion between Logarithmic & Exponential Functions
To understand logarithms, we must first have a firm grasp of exponential functions.
The function f(x) depends on the variable ‘x’. It is often expressed as:
[latex]\Large y=b^x[/latex]
Where ‘b‘ is the base and ‘x‘ is an independent variable. As ‘x‘ increases, the value of ‘y‘ will grow exponentially.
Logarithmic and exponential functions are inversely connected.
where x>0 and b>0, b≠1

The following examples show how to write each equation from logarithmic to exponential form. This can be accomplished by keeping the base the same, converting the logarithmic answer to the exponential power, and the logarithmic argument to the answer of the exponential equation.
Sample Exercises 21.1
Write each equation in exponential form:
- [latex]2 = \text{log}_{5} \, x[/latex]
- [latex]3 = \text{log}_{b} \, 64[/latex]
- [latex]\text{log}_{3} 7 = y[/latex]
- [latex]log_2 \frac{1}{8} = -3[/latex]
- [latex]log_9 \; 3 = \frac{1}{2}[/latex]
Solutions
- [latex]5^{2} = x[/latex]
- [latex]b^{3} = 64[/latex]
- [latex]3^{y} = 7[/latex]
- [latex]2^{-3} = \frac{1}{8}[/latex]
- [latex]3 = 9^{\frac{1}{2}}[/latex]
The following examples show how to write each equation from exponential to logarithmic form. As previously mentioned, keep the base the same, convert the power in the exponential equation to the logarithmic answer, and the the answer of the exponential equation to the logarithmic argument.
Sample Exercises 21.2
Write each equation in logarithmic form:
- [latex]12^{2} = x[/latex]
- [latex]b^{3} = 8[/latex]
- [latex]5^{y} = 9[/latex]
- [latex]4^{2} = 16[/latex]
- [latex]81^{\frac{1}{4}} = 3[/latex]
Solutions
- [latex]2 = \text{log}_{12} \; x[/latex]
- [latex]3 = \text{log}_{b} \; 8[/latex]
- [latex]y = \text{log}_{5} \; 9[/latex]
- [latex]2 = \text{log}_{4} \; 16[/latex]
- [latex]\frac{1}{4} = \text{log}_{81} \; 3[/latex]
Practice Set 21.1: Convert from Logarithmic to Exponential Form
In each of the following practice questions you will be given a logarithmic equation. Convert the equation so that it is expresssed in exponential form.
The answers to this problem set are visible when you click the drop down button below. When you click the word “Answers” you will see the answers for all eight questions.
Questions
- [latex]\text{log}_{12}\; 144 = 2[/latex]
- [latex]4 = \text{log}_2 \; 16[/latex]
- [latex]-2 = \text{log}_6\; \frac{1}{36}[/latex]
- [latex]\frac{1}{2} = \text{log}_9\; 3[/latex]
- [latex]-3 = \text{log} \; 0.001[/latex]
- [latex]\text{log}_3\; \frac{1}{81} = -4[/latex]
- [latex]\text{log}_{25}\; \frac{1}{25} = -1[/latex]
- [latex]\text{log} \; 10000 = 4[/latex]
Answers:
- [latex]12^2 = 144[/latex]
- [latex]2^{4} = 16[/latex]
- [latex]6^{-2} = \frac{1}{36}[/latex]
- [latex]9^{½} = 3[/latex]
- [latex]10^{-3} = 0.001[/latex]
- [latex]3^{-4} = \frac{1}{81}[/latex]
- [latex]25^{-1} = \frac{1}{25}[/latex]
- [latex]10^{4} = 10000[/latex]
Practice Set 21.2: Convert from Exponential to Logarithmic Form
In each of the following practice questions you will be given an exponential equation. Convert the equation so that it is expresssed in logarithmic form.
The answers to this problem set are visible when you click the drop down button below. When you click the word “Answers” you will see the answers for all eight questions.
Questions:
- [latex]3^4 = 81[/latex]
- [latex]5^3 = 125[/latex]
- [latex]2^{-3} = \frac{1}{8}[/latex]
- [latex]27^0 = 1[/latex]
- [latex]3 = 9^{\frac{1}{2}}[/latex]
- [latex]7^{-1} = \frac{1}{7}[/latex]
- [latex]64 = 4^3[/latex]
- [latex]\frac{1}{9} = 3^{-2}[/latex]
Answers:
- [latex]\text{log}_3 \; 81 = 4[/latex]
- [latex]\text{log}_5 \; 125 = 3[/latex]
- [latex]\text{log}_2 \; \frac{1}{8} = -3[/latex]
- [latex]\text{log}_{27} \; 1 = 0[/latex]
- [latex]\text{log}_9 \; 3 = \frac{1}{2}[/latex]
- [latex]\text{log}_7 \; \frac{1}{7} = -1[/latex]
- [latex]\text{log}_4 \; 64 = 3[/latex]
- [latex]\text{log}_3 \; \frac{1}{9} = -2[/latex]
Types of logarithms
There are different types of logarithms, including common logarithms, natural logarithms, logarithms with other bases, as well as antilogarithms.
Common Logarithm
The common logarithm (or standard logarithm) can be considered the inverse (opposite) of 10x. It is the logarithm with the base of 10.
[latex]log_{10}[/latex]
As the common logarithm is widely used, the base is implied and can be written simply as log. So, when there is no base written on the log, you are dealing with the common logarithm which always has a base of 10.
Therefore, [latex]\text{log} \; 1000 = 3[/latex] because [latex]10^{3} = 1000[/latex].
The common log is also the logarithm applied when using the [log] button on your calculator.
Natural Logarithm
The natural logarithm is the inverse of ex. It is the logarithm with the base of ‘e’.
The number ‘e’ is a key mathematical constant that equals: 2.718281828459045… and is referred to as Euler’s number. Just like pi (π), it is an irrational number where the decimals continue on infinitely with no repeating pattern.
Euler’s number is the base of the natural logarithm and is also found on the calculator and applied through the use of the [ln] button.
Natural logarithms follow the same rules as the common logarithm.
Anti-Logarithm
An anti-logarithm or antilog is the inverse of a logarithm. It is the process of raising the base to the power of the logarithm’s result. It can be expressed as either anitlog or log-1.
Example
The antilogarithm of 3 with a base of 10 is 1000.
[latex]\text{antilog} \; 3 = 1000[/latex]The antilog of a number can be found by raising 10 to the power of the same number.
To solve the question: [latex]\text{antilog} \; -2= x[/latex] or alternatively [latex]log^{-1} (-2) = x[/latex]
Simply use the [latex][10^{x}][/latex]button on your calculator. You will see that [latex]10^{2} = 0.01.[/latex]
Similarly, [latex]\text{log} \;x = -2[/latex] can be solved by entering [latex]10^{2}[/latex] into your calculator.
Sample Exercises 21.3
Find each of the following antlogs with your calculator:
- [latex]12^{2} = x[/latex]
- [latex]b^{3} = 8[/latex]
- [latex]5^{y} = 9[/latex]
- [latex]4^{2} = 16[/latex]
- [latex]81^{¼} = 3[/latex]
Solutions
1) [latex]2 = \text{log}_{12} \; x[/latex]
2) [latex]3 = \text{log}_{b} \; 8[/latex]
3) [latex]y = \text{log}_{5} \; 9[/latex]
4) [latex]2 = \text{log}_{4} \; 16[/latex]
5) [latex]\frac{1}{4} = \text{log}_{81} \; 3[/latex]
Practice Set 21.3: Calculate the following logarithms
In each of the following practice questions you will be given an logarithm to solve. With the use of your calculator, determine the correct response. If necessary, round your answer to the nearest ten-thousandths.
The answers to this problem set are visible when you click the drop down button below. When you click the word “Answers” you will see the answers for all eight questions.
Questions:
- [latex]\text{log} \; 100 000[/latex]
- [latex]\text{ln} \;2.718281828[/latex]
- [latex]\text{antilog} \; 0.001[/latex]
- [latex]\text{log} \; 550[/latex]
- [latex]\text{ln} \; 550[/latex]
- [latex]\text{log}^{-1} \; 0.55[/latex]
- [latex]\text{antilog} \; 4.15[/latex]
- [latex]\text{log} \; \frac{3}{8}[/latex]
Answers:
- [latex]\text{log} \;100 000 = 5[/latex]
- [latex]\text{ln} \;2.718281828 = 1.0000[/latex]
- [latex]\text{antilog} \;0.001 = 1.0023[/latex]
- [latex]\text{log} \;550 = 2.7404[/latex]
- [latex]\text{ln} \;550 = 6.3099[/latex]
- [latex]\text{log}^{-1} \;0.55 = 3.5481[/latex]
- [latex]\text{antilog} \;4.05 = 11 220.1845[/latex]
- [latex]\text{log} \; \frac{1}{8} = -0.9031[/latex]
Example
Caution: There is no solution when trying to find the logarithm of a negative number.
[latex]log \;-100[/latex]
Your calculator will show an error because this question can be restated as [latex]10^{x} = -100[/latex], and it is impossible to take 10 and raise it to a power to produce a negative number.
Evaluate logarithms Examples
To solve a logarithmic equation, convert the equation from logarithmic to exponential form.
- [latex]\text{log}_7 \; 49[/latex]
- [latex]\text{log}_2 \; \frac{1}{16}[/latex]
- [latex]\text{log}_4 \; 2[/latex]
Do not use your log button on your calculator to solve any of these problems, as the log button works only with logarithms with a base of 10. These questions have the bases 7, 2, and 4. The easiest approach is to make each of these expressions equal to [latex]x[/latex], change from logarithmic form to exponential form, and then evaluate.
- [latex]\text{log}_7 \; 49 = x[/latex]
[latex]7^x = 49[/latex]
[latex]x = 2[/latex]
[latex]\text{log}_7 \; 49 = 2[/latex] - [latex]\text{log}_2 \; \frac{1}{16}[/latex]
[latex]2^x = \frac{1}{16}[/latex]
[latex]x = -4[/latex]
[latex]\text{log}_2 \; \frac{1}{16} = -4[/latex] - [latex]\text{log}_4 \; 2 = x[/latex]
[latex]4^x = 2[/latex]
[latex]x = \frac{1}{2}[/latex]
[latex]\text{log}_4 \; 2 = \frac{1}{2}[/latex]
Sample Exercises 21.4
Evaluate each of the following logarithms:
- [latex]\text{log}_8 \, 8[/latex]
- [latex]\text{log}_2 \, 32[/latex]
- [latex]\text{log}_{256} \, 4[/latex]
- [latex]\text{log}_8 \, 2[/latex]
- [latex]\text{log}_5 \, \sqrt{5}[/latex]
Solutions
- [latex]\text{log}_8 \, 8 = 1[/latex]
- [latex]\text{log}_2 \, 32 = 5[/latex]
- [latex]\text{log}_{256 } \, 4 = ¼[/latex]
- [latex]\text{log}_8 \, 2 = \frac{1}{3}[/latex]
- [latex]\text{log}_5 \, \sqrt{5} = \frac{1}{2}[/latex]
Converting from logarithmic form to exponential form is a strategy that can be useful to solve for the answer, the base, or the argument of a logarithmic equation.
Examples
a) [latex]log_2\;x = 3[/latex]
[latex]2^3 = x[/latex]
[latex]2^3 = 8[/latex]
b)[latex]log_x\;25 = 2[/latex]
[latex]x^2 = 25[/latex]
[latex]x = 5[/latex]
solving exponential equations
As logarithms are the inverse of exponents, they are particularly useful when you wish to solve for an unknown exponent in an exponential equation.
This can be accomplished using either common log or natural log.
Example
[latex]6^x = 51[/latex] can be solved by restating it as
[latex]x = \frac{log\;51}{log\;6}[/latex]
or
[latex]x = \frac{\text{ln}\; 51}{\text{ln} \; 6}[/latex]
Either way, the response will be:
[latex]x = 2.1944[/latex]
Case Study
Scenario: Evaluating pH and Logarithms
A nurse in a clinic in New Glasgow tests the pH of a sample of a cleaning solution. The concentration of hydrogen ions in the solution is [latex]1 \times 10^{−8} \text{ mol/L.}[/latex] Use the pH formula to calculate the pH of this solution.
Formula: [latex]\text{pH} = −\text{log }[H^{+}][/latex]
Solution
Steps to Solve
- The concentration of hydrogen ions is [latex][H+] = 1 \times 10{−8} \text{ mol/L.}[/latex]
- Use the pH formula: [latex]\text{pH} = −\text{ log }(1\times 10^{−8})[/latex]
- Simplifying: [latex][/latex]\text{pH} = −(−8) = 8[\latex]
Answer
The pH of the solution is 8, which means the solution is basic (alkaline).
Chapter Credit
Chapter (including Case Studies) consists of original content.
Exercises 21.1, 21.2. & 21.3 copied from?

