197
[latexpage]
Learning Objectives
- Define various units of radiation.
- Describe RBE.
We hear many seemingly contradictory things about the biological effects of ionizing radiation. It can cause cancer, burns, and hair loss, yet it is used to treat and even cure cancer. How do we understand these effects? Once again, there is an underlying simplicity in nature, even in complicated biological organisms. All the effects of ionizing radiation on biological tissue can be understood by knowing that ionizing radiation affects molecules within cells, particularly DNA molecules.
Let us take a brief look at molecules within cells and how cells operate. Cells have long, double-helical DNA molecules containing chemical codes called genetic codes that govern the function and processes undertaken by the cell. It is for unraveling the double-helical structure of DNA that James Watson, Francis Crick, and Maurice Wilkins received the Nobel Prize. Damage to DNA consists of breaks in chemical bonds or other changes in the structural features of the DNA chain, leading to changes in the genetic code. In human cells, we can have as many as a million individual instances of damage to DNA per cell per day. It is remarkable that DNA contains codes that check whether the DNA is damaged or can repair itself. It is like an auto check and repair mechanism. This repair ability of DNA is vital for maintaining the integrity of the genetic code and for the normal functioning of the entire organism. It should be constantly active and needs to respond rapidly. The rate of DNA repair depends on various factors such as the cell type and age of the cell. A cell with a damaged ability to repair DNA, which could have been induced by ionizing radiation, can do one of the following:
- The cell can go into an irreversible state of dormancy, known as senescence.
- The cell can commit suicide, known as programmed cell death.
- The cell can go into unregulated cell division leading to tumors and cancers.
Since ionizing radiation damages the DNA, which is critical in cell reproduction, it has its greatest effect on cells that rapidly reproduce, including most types of cancer. Thus, cancer cells are more sensitive to radiation than normal cells and can be killed by it easily. Cancer is characterized by a malfunction of cell reproduction, and can also be caused by ionizing radiation. Without contradiction, ionizing radiation can be both a cure and a cause.
To discuss quantitatively the biological effects of ionizing radiation, we need a radiation dose unit that is directly related to those effects. All effects of radiation are assumed to be directly proportional to the amount of ionization produced in the biological organism. The amount of ionization is in turn proportional to the amount of deposited energy. Therefore, we define a radiation dose unit called the rad, as \(1/100\) of a joule of ionizing energy deposited per kilogram of tissue, which is
For example, if a 50.0-kg person is exposed to ionizing radiation over her entire body and she absorbs 1.00 J, then her whole-body radiation dose is
If the same 1.00 J of ionizing energy were absorbed in her 2.00-kg forearm alone, then the dose to the forearm would be
and the unaffected tissue would have a zero rad dose. While calculating radiation doses, you divide the energy absorbed by the mass of affected tissue. You must specify the affected region, such as the whole body or forearm in addition to giving the numerical dose in rads. The SI unit for radiation dose is the gray (Gy), which is defined to be
However, the rad is still commonly used. Although the energy per kilogram in 1 rad is small, it has significant effects since the energy causes ionization. The energy needed for a single ionization is a few eV, or less than \({\text{10}}^{-\text{18}}\phantom{\rule{0.25em}{0ex}}\text{J}\). Thus, 0.01 J of ionizing energy can create a huge number of ion pairs and have an effect at the cellular level.
The effects of ionizing radiation may be directly proportional to the dose in rads, but they also depend on the type of radiation and the type of tissue. That is, for a given dose in rads, the effects depend on whether the radiation is \(\mathrm{\alpha ,}\phantom{\rule{0.25em}{0ex}}\mathrm{\beta ,}\phantom{\rule{0.25em}{0ex}}\mathrm{\gamma ,}\) x-ray, or some other type of ionizing radiation. In the earlier discussion of the range of ionizing radiation, it was noted that energy is deposited in a series of ionizations and not in a single interaction. Each ion pair or ionization requires a certain amount of energy, so that the number of ion pairs is directly proportional to the amount of the deposited ionizing energy. But, if the range of the radiation is small, as it is for \(\alpha \) s, then the ionization and the damage created is more concentrated and harder for the organism to repair, as seen in (Figure). Concentrated damage is more difficult for biological organisms to repair than damage that is spread out, so short-range particles have greater biological effects. The relative biological effectiveness (RBE) or quality factor (QF) is given in (Figure) for several types of ionizing radiation—the effect of the radiation is directly proportional to the RBE. A dose unit more closely related to effects in biological tissue is called the roentgen equivalent man or rem and is defined to be the dose in rads multiplied by the relative biological effectiveness.
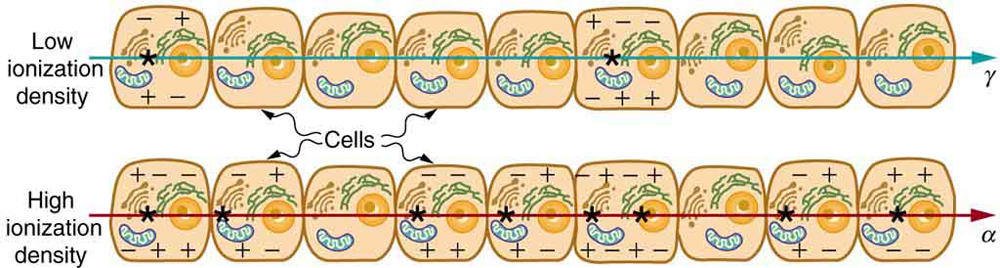
So, if a person had a whole-body dose of 2.00 rad of \(\gamma \) radiation, the dose in rem would be \(\text{(2.00 rad)(1) = 2.00 rem whole body}\). If the person had a whole-body dose of 2.00 rad of \(\alpha \) radiation, then the dose in rem would be \(\text{(2.00 rad)(20) = 40.0 rem whole body}\). The \(\alpha \) s would have 20 times the effect on the person than the \(\gamma \) s for the same deposited energy. The SI equivalent of the rem is the sievert (Sv), defined to be \(\text{Sv}=\text{Gy}×\text{RBE}\), so that
The RBEs given in (Figure) are approximate, but they yield certain insights. For example, the eyes are more sensitive to radiation, because the cells of the lens do not repair themselves. Neutrons cause more damage than \(\gamma \) rays, although both are neutral and have large ranges, because neutrons often cause secondary radiation when they are captured. Note that the RBEs are 1 for higher-energy \(\beta \) s, \(\gamma \) s, and x-rays, three of the most common types of radiation. For those types of radiation, the numerical values of the dose in rem and rad are identical. For example, 1 rad of \(\gamma \) radiation is also 1 rem. For that reason, rads are still widely quoted rather than rem. (Figure) summarizes the units that are used for radiation.
“Activity” refers to the radioactive source while “dose” refers to the amount of energy from the radiation that is deposited in a person or object.
A high level of activity doesn’t mean much if a person is far away from the source. The activity \(R\) of a source depends upon the quantity of material (kg) as well as the half-life. A short half-life will produce many more disintegrations per second. Recall that \(R=\frac{\text{0.693}N}{{t}_{1/2}}\). Also, the activity decreases exponentially, which is seen in the equation \(R={R}_{0}{e}^{-\mathrm{\lambda t}}\).
| Type and energy of radiation | RBE1 |
|---|---|
| X-rays | 1 |
| \(\gamma \) rays | 1 |
| \(\beta \) rays greater than 32 keV | 1 |
| \(\beta \)rays less than 32 keV | 1.7 |
| Neutrons, thermal to slow (<20 keV) | 2–5 |
| Neutrons, fast (1–10 MeV) | 10 (body), 32 (eyes) |
| Protons (1–10 MeV) | 10 (body), 32 (eyes) |
| \(\alpha \) rays from radioactive decay | 10–20 |
| Heavy ions from accelerators | 10–20 |
| Quantity | SI unit name | Definition | Former unit | Conversion |
|---|---|---|---|---|
| Activity | Becquerel (bq) | decay/s | Curie (Ci) | \(1 Bq = 2\text{.}7×{\text{10}}^{-\text{11}}\phantom{\rule{0.25em}{0ex}}\text{Ci}\) |
| Absorbed dose | Gray (Gy) | 1 J/kg | rad | \(\text{Gy = 100 rad}\) |
| Dose Equivalent | Sievert (Sv) | 1 J/kg × RBE | rem | \(\text{Sv = 100 rem}\) |
The large-scale effects of radiation on humans can be divided into two categories: immediate effects and long-term effects. (Figure) gives the immediate effects of whole-body exposures received in less than one day. If the radiation exposure is spread out over more time, greater doses are needed to cause the effects listed. This is due to the body’s ability to partially repair the damage. Any dose less than 100 mSv (10 rem) is called a low dose, 0.1 Sv to 1 Sv (10 to 100 rem) is called a moderate dose, and anything greater than 1 Sv (100 rem) is called a high dose. There is no known way to determine after the fact if a person has been exposed to less than 10 mSv.
| Dose in Sv 2 | Effect |
|---|---|
| 0–0.10 | No observable effect. |
| 0.1 – 1 | Slight to moderate decrease in white blood cell counts. |
| 0.5 | Temporary sterility; 0.35 for women, 0.50 for men. |
| 1 – 2 | Significant reduction in blood cell counts, brief nausea and vomiting. Rarely fatal. |
| 2 – 5 | Nausea, vomiting, hair loss, severe blood damage, hemorrhage, fatalities. |
| 4.5 | LD50/32. Lethal to 50% of the population within 32 days after exposure if not treated. |
| 5 – 20 | Worst effects due to malfunction of small intestine and blood systems. Limited survival. |
| >20 | Fatal within hours due to collapse of central nervous system. |
Immediate effects are explained by the effects of radiation on cells and the sensitivity of rapidly reproducing cells to radiation. The first clue that a person has been exposed to radiation is a change in blood count, which is not surprising since blood cells are the most rapidly reproducing cells in the body. At higher doses, nausea and hair loss are observed, which may be due to interference with cell reproduction. Cells in the lining of the digestive system also rapidly reproduce, and their destruction causes nausea. When the growth of hair cells slows, the hair follicles become thin and break off. High doses cause significant cell death in all systems, but the lowest doses that cause fatalities do so by weakening the immune system through the loss of white blood cells.
The two known long-term effects of radiation are cancer and genetic defects. Both are directly attributable to the interference of radiation with cell reproduction. For high doses of radiation, the risk of cancer is reasonably well known from studies of exposed groups. Hiroshima and Nagasaki survivors and a smaller number of people exposed by their occupation, such as radium dial painters, have been fully documented. Chernobyl victims will be studied for many decades, with some data already available. For example, a significant increase in childhood thyroid cancer has been observed. The risk of a radiation-induced cancer for low and moderate doses is generally assumed to be proportional to the risk known for high doses. Under this assumption, any dose of radiation, no matter how small, involves a risk to human health. This is called the linear hypothesis and it may be prudent, but it is controversial. There is some evidence that, unlike the immediate effects of radiation, the long-term effects are cumulative and there is little self-repair. This is analogous to the risk of skin cancer from UV exposure, which is known to be cumulative.
There is a latency period for the onset of radiation-induced cancer of about 2 years for leukemia and 15 years for most other forms. The person is at risk for at least 30 years after the latency period. Omitting many details, the overall risk of a radiation-induced cancer death per year per rem of exposure is about 10 in a million, which can be written as \(\text{10}/{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{rem}\phantom{\rule{0.25em}{0ex}}\text{·}\phantom{\rule{0.25em}{0ex}}\text{y}\).
If a person receives a dose of 1 rem, his risk each year of dying from radiation-induced cancer is 10 in a million and that risk continues for about 30 years. The lifetime risk is thus 300 in a million, or 0.03 percent. Since about 20 percent of all worldwide deaths are from cancer, the increase due to a 1 rem exposure is impossible to detect demographically. But 100 rem (1 Sv), which was the dose received by the average Hiroshima and Nagasaki survivor, causes a 3 percent risk, which can be observed in the presence of a 20 percent normal or natural incidence rate.
The incidence of genetic defects induced by radiation is about one-third that of cancer deaths, but is much more poorly known. The lifetime risk of a genetic defect due to a 1 rem exposure is about 100 in a million or \(3\text{.}3/{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{rem}\cdot \text{y}\), but the normal incidence is 60,000 in a million. Evidence of such a small increase, tragic as it is, is nearly impossible to obtain. For example, there is no evidence of increased genetic defects among the offspring of Hiroshima and Nagasaki survivors. Animal studies do not seem to correlate well with effects on humans and are not very helpful. For both cancer and genetic defects, the approach to safety has been to use the linear hypothesis, which is likely to be an overestimate of the risks of low doses. Certain researchers even claim that low doses are beneficial. Hormesis is a term used to describe generally favorable biological responses to low exposures of toxins or radiation. Such low levels may help certain repair mechanisms to develop or enable cells to adapt to the effects of the low exposures. Positive effects may occur at low doses that could be a problem at high doses.
Even the linear hypothesis estimates of the risks are relatively small, and the average person is not exposed to large amounts of radiation. (Figure) lists average annual background radiation doses from natural and artificial sources for Australia, the United States, Germany, and world-wide averages. Cosmic rays are partially shielded by the atmosphere, and the dose depends upon altitude and latitude, but the average is about 0.40 mSv/y. A good example of the variation of cosmic radiation dose with altitude comes from the airline industry. Monitored personnel show an average of 2 mSv/y. A 12-hour flight might give you an exposure of 0.02 to 0.03 mSv.
Doses from the Earth itself are mainly due to the isotopes of uranium, thorium, and potassium, and vary greatly by location. Some places have great natural concentrations of uranium and thorium, yielding doses ten times as high as the average value. Internal doses come from foods and liquids that we ingest. Fertilizers containing phosphates have potassium and uranium. So we are all a little radioactive. Carbon-14 has about 66 Bq/kg radioactivity whereas fertilizers may have more than 3000 Bq/kg radioactivity. Medical and dental diagnostic exposures are mostly from x-rays. It should be noted that x-ray doses tend to be localized and are becoming much smaller with improved techniques. (Figure) shows typical doses received during various diagnostic x-ray examinations. Note the large dose from a CT scan. While CT scans only account for less than 20 percent of the x-ray procedures done today, they account for about 50 percent of the annual dose received.
Radon is usually more pronounced underground and in buildings with low air exchange with the outside world. Almost all soil contains some \({}^{\text{226}}\text{Ra}\) and \({}^{\text{222}}\text{Rn}\), but radon is lower in mainly sedimentary soils and higher in granite soils. Thus, the exposure to the public can vary greatly, even within short distances. Radon can diffuse from the soil into homes, especially basements. The estimated exposure for \({}^{\text{222}}\text{Rn}\) is controversial. Recent studies indicate there is more radon in homes than had been realized, and it is speculated that radon may be responsible for 20 percent of lung cancers, being particularly hazardous to those who also smoke. Many countries have introduced limits on allowable radon concentrations in indoor air, often requiring the measurement of radon concentrations in a house prior to its sale. Ironically, it could be argued that the higher levels of radon exposure and their geographic variability, taken with the lack of demographic evidence of any effects, means that low-level radiation is less dangerous than previously thought.
Radiation Protection
Laws regulate radiation doses to which people can be exposed. The greatest occupational whole-body dose that is allowed depends upon the country and is about 20 to 50 mSv/y and is rarely reached by medical and nuclear power workers. Higher doses are allowed for the hands. Much lower doses are permitted for the reproductive organs and the fetuses of pregnant women. Inadvertent doses to the public are limited to \(1/\text{10}\) of occupational doses, except for those caused by nuclear power, which cannot legally expose the public to more than \(1/\text{1000}\) of the occupational limit or 0.05 mSv/y (5 mrem/y). This has been exceeded in the United States only at the time of the Three Mile Island (TMI) accident in 1979. Chernobyl is another story. Extensive monitoring with a variety of radiation detectors is performed to assure radiation safety. Increased ventilation in uranium mines has lowered the dose there to about 1 mSv/y.
| Source | Dose (mSv/y)3 | |||
|---|---|---|---|---|
| Source | Australia | Germany | United States | World |
| Natural Radiation – external | ||||
| Cosmic Rays | 0.30 | 0.28 | 0.30 | 0.39 |
| Soil, building materials | 0.40 | 0.40 | 0.30 | 0.48 |
| Radon gas | 0.90 | 1.1 | 2.0 | 1.2 |
| Natural Radiation – internal | ||||
| \({}^{\text{40}}\text{K,}\phantom{\rule{0.25em}{0ex}}{}^{\text{14}}\text{C,}\phantom{\rule{0.25em}{0ex}}{}^{\text{226}}\text{Ra}\) | 0.24 | 0.28 | 0.40 | 0.29 |
| Medical & Dental | 0.80 | 0.90 | 0.53 | 0.40 |
| TOTAL | 2.6 | 3.0 | 3.5 | 2.8 |
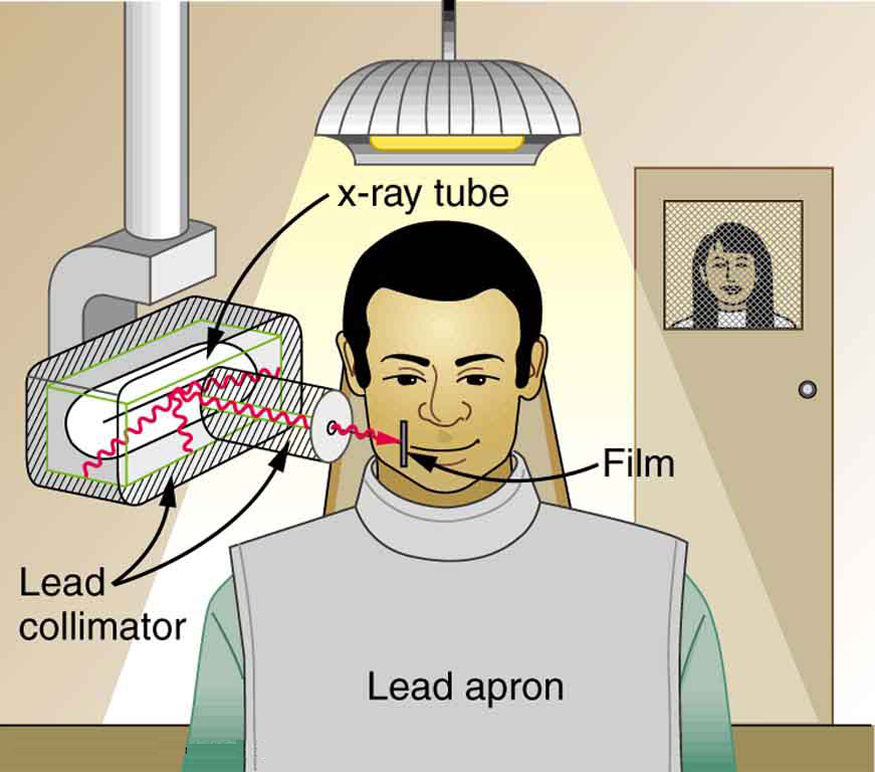
To physically limit radiation doses, we use shielding, increase the distance from a source, and limit the time of exposure.
(Figure) illustrates how these are used to protect both the patient and the dental technician when an x-ray is taken. Shielding absorbs radiation and can be provided by any material, including sufficient air. The greater the distance from the source, the more the radiation spreads out. The less time a person is exposed to a given source, the smaller is the dose received by the person. Doses from most medical diagnostics have decreased in recent years due to faster films that require less exposure time.
| Procedure | Effective dose (mSv) |
|---|---|
| Chest | 0.02 |
| Dental | 0.01 |
| Skull | 0.07 |
| Leg | 0.02 |
| Mammogram | 0.40 |
| Barium enema | 7.0 |
| Upper GI | 3.0 |
| CT head | 2.0 |
| CT abdomen | 10.0 |
Problem-Solving Strategy
You need to follow certain steps for dose calculations, which are
Step 1. Examine the situation to determine that a person is exposed to ionizing radiation.
Step 2. Identify exactly what needs to be determined in the problem (identify the unknowns). The most straightforward problems ask for a dose calculation.
Step 3. Make a list of what is given or can be inferred from the problem as stated (identify the knowns). Look for information on the type of radiation, the energy per event, the activity, and the mass of tissue affected.
Step 4. For dose calculations, you need to determine the energy deposited. This may take one or more steps, depending on the given information.
Step 5. Divide the deposited energy by the mass of the affected tissue. Use units of joules for energy and kilograms for mass. If a dose in Sv is involved, use the definition that \(\text{1 Sv = 1 J/kg}\).
Step 6. If a dose in mSv is involved, determine the RBE (QF) of the radiation. Recall that \(1 mSv=1 mGy×\text{RBE}\phantom{\rule{0.25em}{0ex}}\left(\text{or}\phantom{\rule{0.25em}{0ex}}1 rem=1 rad×\text{RBE}\right)\).
Step 7. Check the answer to see if it is reasonable: Does it make sense? The dose should be consistent with the numbers given in the text for diagnostic, occupational, and therapeutic exposures.
Calculate the dose in rem/y for the lungs of a weapons plant employee who inhales and retains an activity of \(\text{1.00 μCi of}\phantom{\rule{0.25em}{0ex}}{}^{\text{239}}\text{Pu}\) in an accident. The mass of affected lung tissue is 2.00 kg, the plutonium decays by emission of a 5.23-MeV \(\alpha \) particle, and you may assume the higher value of the RBE for \(\alpha \) s from (Figure).
Strategy
Dose in rem is defined by \(\text{1 rad}=0\text{.}\text{01 J/kg}\) and \(\text{rem}=\text{rad}×\text{RBE}\). The energy deposited is divided by the mass of tissue affected and then multiplied by the RBE. The latter two quantities are given, and so the main task in this example will be to find the energy deposited in one year. Since the activity of the source is given, we can calculate the number of decays, multiply by the energy per decay, and convert MeV to joules to get the total energy.
Solution
The activity \(R=1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{μCi}=\text{3}\text{.}\text{70}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{Bq}=3\text{.}\text{70}×{\text{10}}^{4}\) decays/s. So, the number of decays per year is obtained by multiplying by the number of seconds in a year:
Thus, the ionizing energy deposited per year is
Dividing by the mass of the affected tissue gives
One Gray is 1.00 J/kg, and so the dose in Gy is
Now, the dose in Sv is
Discussion
First note that the dose is given to two digits, because the RBE is (at best) known only to two digits. By any standard, this yearly radiation dose is high and will have a devastating effect on the health of the worker. Worse yet, plutonium has a long radioactive half-life and is not readily eliminated by the body, and so it will remain in the lungs. Being an \(\alpha \) emitter makes the effects 10 to 20 times worse than the same ionization produced by \(\beta \) s, \(\gamma \) rays, or x-rays. An activity of \(1.00\phantom{\rule{0.25em}{0ex}}\mu Ci\) is created by only \(16\phantom{\rule{0.25em}{0ex}}\mu g\) of \({}^{\text{239}}\text{Pu}\) (left as an end-of-chapter problem to verify), partly justifying claims that plutonium is the most toxic substance known. Its actual hazard depends on how likely it is to be spread out among a large population and then ingested. The Chernobyl disaster’s deadly legacy, for example, has nothing to do with the plutonium it put into the environment.
Risk versus Benefit
Medical doses of radiation are also limited. Diagnostic doses are generally low and have further lowered with improved techniques and faster films. With the possible exception of routine dental x-rays, radiation is used diagnostically only when needed so that the low risk is justified by the benefit of the diagnosis. Chest x-rays give the lowest doses—about 0.1 mSv to the tissue affected, with less than 5 percent scattering into tissues that are not directly imaged. Other x-ray procedures range upward to about 10 mSv in a CT scan, and about 5 mSv (0.5 rem) per dental x-ray, again both only affecting the tissue imaged. Medical images with radiopharmaceuticals give doses ranging from 1 to 5 mSv, usually localized. One exception is the thyroid scan using \({}^{\text{131}}\text{I}\). Because of its relatively long half-life, it exposes the thyroid to about 0.75 Sv. The isotope \({}^{\text{123}}\text{I}\) is more difficult to produce, but its short half-life limits thyroid exposure to about 15 mSv.
Watch alpha particles escape from a polonium nucleus, causing radioactive alpha decay. See how random decay times relate to the half life. Click to open media in new browser.
Section Summary
- The biological effects of ionizing radiation are due to two effects it has on cells: interference with cell reproduction, and destruction of cell function.
- A radiation dose unit called the rad is defined in terms of the ionizing energy deposited per kilogram of tissue:
\(1 rad=\text{0.01 J/kg}.\)
- The SI unit for radiation dose is the gray (Gy), which is defined to be \(1 Gy = 1 J/kg = 100 rad.\)
- To account for the effect of the type of particle creating the ionization, we use the relative biological effectiveness (RBE) or quality factor (QF) given in (Figure) and define a unit called the roentgen equivalent man (rem) as
\(\text{rem}=\text{rad}×\text{RBE}.\)
- Particles that have short ranges or create large ionization densities have RBEs greater than unity. The SI equivalent of the rem is the sievert (Sv), defined to be
\(\text{Sv}=\text{Gy}×\text{RBE}\text{ and 1 Sv}=1\text{00 rem.}\)
- Whole-body, single-exposure doses of 0.1 Sv or less are low doses while those of 0.1 to 1 Sv are moderate, and those over 1 Sv are high doses. Some immediate radiation effects are given in (Figure). Effects due to low doses are not observed, but their risk is assumed to be directly proportional to those of high doses, an assumption known as the linear hypothesis. Long-term effects are cancer deaths at the rate of \(\text{10}/{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{rem·y}\)and genetic defects at roughly one-third this rate. Background radiation doses and sources are given in (Figure). World-wide average radiation exposure from natural sources, including radon, is about 3 mSv, or 300 mrem. Radiation protection utilizes shielding, distance, and time to limit exposure.
Conceptual Questions
Isotopes that emit \(\alpha \) radiation are relatively safe outside the body and exceptionally hazardous inside. Yet those that emit \(\gamma \) radiation are hazardous outside and inside. Explain why.
Why is radon more closely associated with inducing lung cancer than other types of cancer?
The RBE for low-energy \(\beta \)s is 1.7, whereas that for higher-energy \(\beta \)s is only 1. Explain why, considering how the range of radiation depends on its energy.
Which methods of radiation protection were used in the device shown in the first photo in (Figure)? Which were used in the situation shown in the second photo?
(a)

What radioisotope could be a problem in homes built of cinder blocks made from uranium mine tailings? (This is true of homes and schools in certain regions near uranium mines.)
Are some types of cancer more sensitive to radiation than others? If so, what makes them more sensitive?
Suppose a person swallows some radioactive material by accident. What information is needed to be able to assess possible damage?
Problems & Exercises
What is the dose in mSv for: (a) a 0.1 Gy x-ray? (b) 2.5 mGy of neutron exposure to the eye? (c) 1.5 mGy of \(\alpha \) exposure?
(a) 100 mSv
(b) 80 mSv
(c) ~30 mSv
Find the radiation dose in Gy for: (a) A 10-mSv fluoroscopic x-ray series. (b) 50 mSv of skin exposure by an \(\alpha \) emitter. (c) 160 mSv of \({\beta }^{–}\) and \(\gamma \) rays from the \({}^{\text{40}}\text{K}\) in your body.
How many Gy of exposure is needed to give a cancerous tumor a dose of 40 Sv if it is exposed to \(\alpha \) activity?
~2 Gy
What is the dose in Sv in a cancer treatment that exposes the patient to 200 Gy of \(\gamma \) rays?
One half the \(\gamma \) rays from \({}^{\text{99m}}\text{Tc}\) are absorbed by a 0.170-mm-thick lead shielding. Half of the \(\gamma \) rays that pass through the first layer of lead are absorbed in a second layer of equal thickness. What thickness of lead will absorb all but one in 1000 of these \(\gamma \) rays?
1.69 mm
A plumber at a nuclear power plant receives a whole-body dose of 30 mSv in 15 minutes while repairing a crucial valve. Find the radiation-induced yearly risk of death from cancer and the chance of genetic defect from this maximum allowable exposure.
In the 1980s, the term picowave was used to describe food irradiation in order to overcome public resistance by playing on the well-known safety of microwave radiation. Find the energy in MeV of a photon having a wavelength of a picometer.
1.24 MeV
Find the mass of \({}^{\text{239}}\text{Pu}\) that has an activity of \(\text{1.00 μCi}\).
Footnotes
Glossary
- gray (Gy)
- the SI unit for radiation dose which is defined to be \(1 Gy=1 J/kg=\text{100 rad}\)
- linear hypothesis
- assumption that risk is directly proportional to risk from high doses
- rad
- the ionizing energy deposited per kilogram of tissue
- sievert
- the SI equivalent of the rem
- relative biological effectiveness (RBE)
- a number that expresses the relative amount of damage that a fixed amount of ionizing radiation of a given type can inflict on biological tissues
- quality factor
- same as relative biological effectiveness
- roentgen equivalent man (rem)
- a dose unit more closely related to effects in biological tissue
- low dose
- a dose less than 100 mSv (10 rem)
- moderate dose
- a dose from 0.1 Sv to 1 Sv (10 to 100 rem)
- high dose
- a dose greater than 1 Sv (100 rem)
- hormesis
- a term used to describe generally favorable biological responses to low exposures of toxins or radiation
- shielding
- a technique to limit radiation exposure

