75

[latexpage]

Learning Objectives

  • Identify a Carnot cycle.
  • Calculate maximum theoretical efficiency of a nuclear reactor.
  • Explain how dissipative processes affect the ideal Carnot engine.
This novelty toy, known as the drinking bird, is an example of Carnot’s engine. It contains methylene chloride (mixed with a dye) in the abdomen, which boils at a very low temperature—about \(\text{100ºF}\). To operate, one gets the bird’s head wet. As the water evaporates, fluid moves up into the head, causing the bird to become top-heavy and dip forward back into the water. This cools down the methylene chloride in the head, and it moves back into the abdomen, causing the bird to become bottom heavy and tip up. Except for a very small input of energy—the original head-wetting—the bird becomes a perpetual motion machine of sorts. (credit: Arabesk.nl, Wikimedia Commons)

Photograph of a novelty toy known as the drinking bird. It is made up of two glass bulbs connected to each other by a glass tube. The upper bulb is shaped like a bird’s head, and the tube looks like its neck. The lower bulb, which may be compared to the abdomen, contains methylene chloride that has been colored red. The bottom of the neck is attached to a pivot, and in front of the bird’s head is a glass of water.

We know from the second law of thermodynamics that a heat engine cannot be 100% efficient, since there must always be some heat transfer \({Q}_{\text{c}}\) to the environment, which is often called waste heat. How efficient, then, can a heat engine be? This question was answered at a theoretical level in 1824 by a young French engineer, Sadi Carnot (1796–1832), in his study of the then-emerging heat engine technology crucial to the Industrial Revolution. He devised a theoretical cycle, now called the Carnot cycle, which is the most efficient cyclical process possible. The second law of thermodynamics can be restated in terms of the Carnot cycle, and so what Carnot actually discovered was this fundamental law. Any heat engine employing the Carnot cycle is called a Carnot engine.

What is crucial to the Carnot cycle—and, in fact, defines it—is that only reversible processes are used. Irreversible processes involve dissipative factors, such as friction and turbulence. This increases heat transfer \({Q}_{\text{c}}\) to the environment and reduces the efficiency of the engine. Obviously, then, reversible processes are superior.

Carnot Engine

Stated in terms of reversible processes, the second law of thermodynamics has a third form:

A Carnot engine operating between two given temperatures has the greatest possible efficiency of any heat engine operating between these two temperatures. Furthermore, all engines employing only reversible processes have this same maximum efficiency when operating between the same given temperatures.

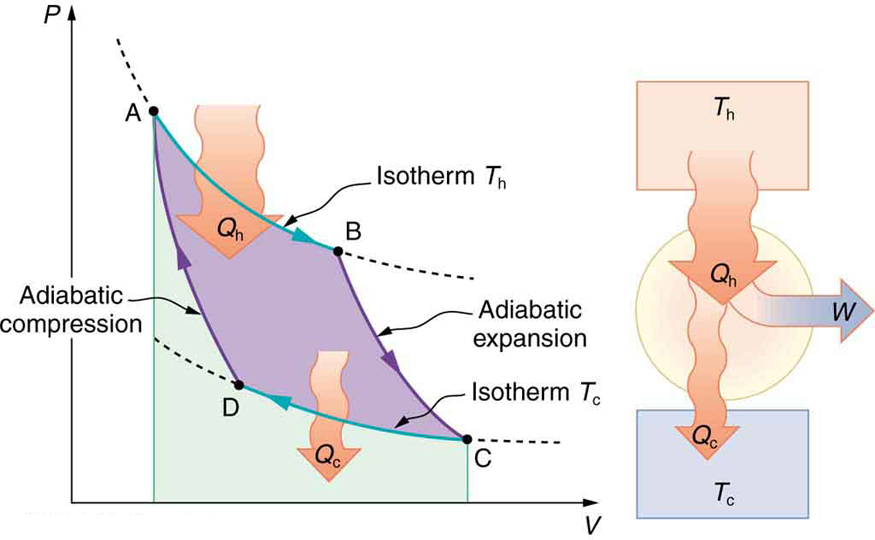
(Figure) shows the \(\text{PV}\) diagram for a Carnot cycle. The cycle comprises two isothermal and two adiabatic processes. Recall that both isothermal and adiabatic processes are, in principle, reversible.

Carnot also determined the efficiency of a perfect heat engine—that is, a Carnot engine. It is always true that the efficiency of a cyclical heat engine is given by:

\(\text{Eff}=\frac{{Q}_{\text{h}}-{Q}_{\text{c}}}{{Q}_{\text{h}}}=1-\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}\text{.}\)

What Carnot found was that for a perfect heat engine, the ratio \({Q}_{\text{c}}/{Q}_{\text{h}}\) equals the ratio of the absolute temperatures of the heat reservoirs. That is, \({Q}_{\text{c}}/{Q}_{\text{h}}={T}_{\text{c}}/{T}_{\text{h}}\) for a Carnot engine, so that the maximum or Carnot efficiency \({\mathrm{Eff}}_{\text{C}}\) is given by

\({\mathrm{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}\text{,}\)

where \({T}_{\text{h}}\) and \({T}_{\text{c}}\) are in kelvins (or any other absolute temperature scale). No real heat engine can do as well as the Carnot efficiency—an actual efficiency of about 0.7 of this maximum is usually the best that can be accomplished. But the ideal Carnot engine, like the drinking bird above, while a fascinating novelty, has zero power. This makes it unrealistic for any applications.

Carnot’s interesting result implies that 100% efficiency would be possible only if \({T}_{\text{c}}=0 K\) —that is, only if the cold reservoir were at absolute zero, a practical and theoretical impossibility. But the physical implication is this—the only way to have all heat transfer go into doing work is to remove all thermal energy, and this requires a cold reservoir at absolute zero.

It is also apparent that the greatest efficiencies are obtained when the ratio \({T}_{\text{c}}/{T}_{\text{h}}\) is as small as possible. Just as discussed for the Otto cycle in the previous section, this means that efficiency is greatest for the highest possible temperature of the hot reservoir and lowest possible temperature of the cold reservoir. (This setup increases the area inside the closed loop on the \(\text{PV}\) diagram; also, it seems reasonable that the greater the temperature difference, the easier it is to divert the heat transfer to work.) The actual reservoir temperatures of a heat engine are usually related to the type of heat source and the temperature of the environment into which heat transfer occurs. Consider the following example.

\(\text{PV}\) diagram for a Carnot cycle, employing only reversible isothermal and adiabatic processes. Heat transfer \({Q}_{\text{h}}\) occurs into the working substance during the isothermal path AB, which takes place at constant temperature \({T}_{\text{h}}\). Heat transfer \({Q}_{\text{c}}\) occurs out of the working substance during the isothermal path CD, which takes place at constant temperature \({T}_{\text{c}}\). The net work output \(W\) equals the area inside the path ABCDA. Also shown is a schematic of a Carnot engine operating between hot and cold reservoirs at temperatures \({T}_{\text{h}}\) and \({T}_{\text{c}}\). Any heat engine using reversible processes and operating between these two temperatures will have the same maximum efficiency as the Carnot engine.

Part a of the figure shows a graph of pressure P versus volume V for a Carnot cycle. The pressure P is along the Y axis and the volume V is along the X axis. The graph shows a complete cycle A B C D. The path begins at point A, then it moves smoothly down till point B along the direction of the X axis. This is marked as an isotherm at temperature T sub h. Then the curve drops down further, along a different curve, from point B to point C. This is marked as adiabatic expansion. The curve rises from point C to point D along the direction opposite to that of A B. This is also an isotherm but at temperature T sub c. The last part of the curve rises up from point D back to A along a direction opposite to that of B C. This is marked as adiabatic compression. The path C D is lower than path A B. Heat Q sub h enters the system, as shown by a bold arrow to the curve A B. Heat Q sub c leaves the system as shown by a bold arrow near C D. Part b of the diagram shows an internal combustion engine represented as a circle. The hot reservoir is a rectangular section at the top of the circle shown at temperature T sub h. A cold reservoir is shown as a rectangular section in the bottom part of the circle at temperature T sub c. Heat Q sub h enters the heat engine as shown by a bold arrow; work W is produced as output, shown to leave the system, and the remaining heat Q sub c is returned back to the cold reservoir, as shown by a bold arrow toward it.

Maximum Theoretical Efficiency for a Nuclear Reactor

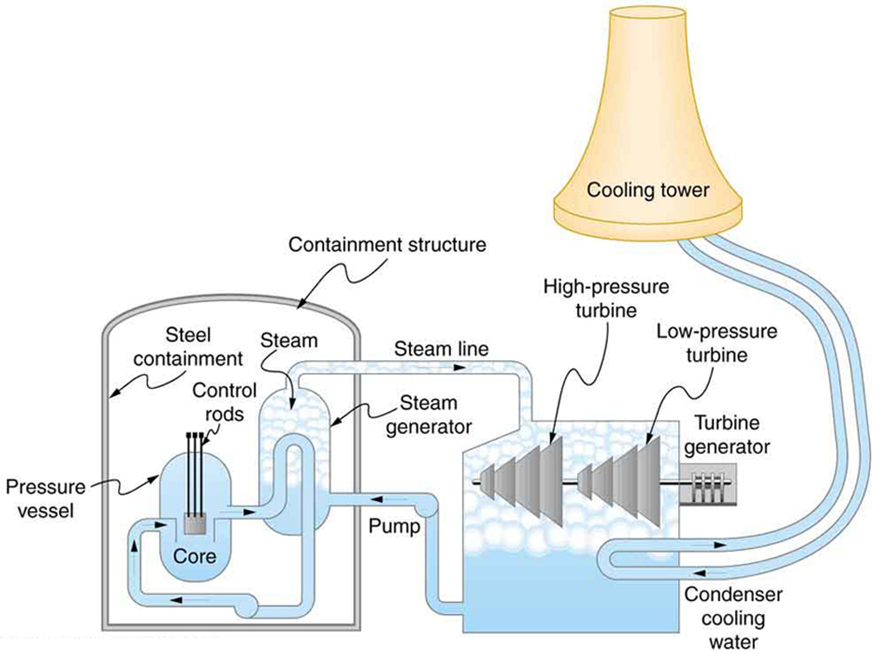
A nuclear power reactor has pressurized water at \(\text{300}\text{º}\text{C}\). (Higher temperatures are theoretically possible but practically not, due to limitations with materials used in the reactor.) Heat transfer from this water is a complex process (see (Figure)). Steam, produced in the steam generator, is used to drive the turbine-generators. Eventually the steam is condensed to water at \(\text{27}\text{º}\text{C}\) and then heated again to start the cycle over. Calculate the maximum theoretical efficiency for a heat engine operating between these two temperatures.

Schematic diagram of a pressurized water nuclear reactor and the steam turbines that convert work into electrical energy. Heat exchange is used to generate steam, in part to avoid contamination of the generators with radioactivity. Two turbines are used because this is less expensive than operating a single generator that produces the same amount of electrical energy. The steam is condensed to liquid before being returned to the heat exchanger, to keep exit steam pressure low and aid the flow of steam through the turbines (equivalent to using a lower-temperature cold reservoir). The considerable energy associated with condensation must be dissipated into the local environment; in this example, a cooling tower is used so there is no direct heat transfer to an aquatic environment. (Note that the water going to the cooling tower does not come into contact with the steam flowing over the turbines.)

Diagram shows a schematic diagram of a pressurized water nuclear reactor and the steam turbines that convert work into electrical energy. There is a pressure vessel in the middle, dome shaped at the ends. This has a nuclear core in it. The core is a small square in the center of the reactor. Control rods are shown as sticks of equal length attached to the core. The pressure vessel has some coolant tubes passing through it and then back to a steam chamber. These coolant tubes contain a coolant liquid that transports the heat from the pressure vessel to the steam chamber. This whole system is enclosed in another dome shaped containment structure of steel. The water supply to steam chamber and the steam outlet are seen to come out of this chamber. This steam is now shown to run two steam turbines, one a high pressure one and another low pressure one. The turbines are nearly triangular and segmented in shape. The steam turbine in turn generates power using a turbine generator, which is attached to the turbine system. The turbines are again housed in another chamber which gets the steam from the steam chamber and return the steam as water back to the steam chamber with pipes. A coolant tower is shown near the turbine system, which is shown to supply cool water in tubes to the turbine system to cool the steam back to water.

Strategy

Since temperatures are given for the hot and cold reservoirs of this heat engine, \({\mathrm{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}\) can be used to calculate the Carnot (maximum theoretical) efficiency. Those temperatures must first be converted to kelvins.

Solution

The hot and cold reservoir temperatures are given as \(\text{300}\text{º}\text{C}\) and \(\text{27}\text{.}0\text{º}\text{C}\), respectively. In kelvins, then, \({T}_{\text{h}}=\text{573 K}\) and \({T}_{\text{c}}=\text{300 K}\), so that the maximum efficiency is

\({\text{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}\text{.}\)

Thus,

\(\begin{array}{lll}{\text{Eff}}_{\text{C}}& =& 1-\frac{\text{300 K}}{\text{573 K}}\\ & =& 0\text{.}\text{476}\text{, or }\text{47}\text{.}6%\text{.}\end{array}\)

Discussion

A typical nuclear power station’s actual efficiency is about 35%, a little better than 0.7 times the maximum possible value, a tribute to superior engineering. Electrical power stations fired by coal, oil, and natural gas have greater actual efficiencies (about 42%), because their boilers can reach higher temperatures and pressures. The cold reservoir temperature in any of these power stations is limited by the local environment. (Figure) shows (a) the exterior of a nuclear power station and (b) the exterior of a coal-fired power station. Both have cooling towers into which water from the condenser enters the tower near the top and is sprayed downward, cooled by evaporation.

(a) A nuclear power station (credit: BlatantWorld.com) and (b) a coal-fired power station. Both have cooling towers in which water evaporates into the environment, representing \({Q}_{\text{c}}\). The nuclear reactor, which supplies \({Q}_{\text{h}}\), is housed inside the dome-shaped containment buildings. (credit: Robert & Mihaela Vicol, publicphoto.org)

Part a shows a photograph of an operational nuclear power plant in night view. There are dome shaped structures which house radioactive material and vapors are shown to come from two cooling towers. Part b shows a photograph of a coal fired power plant. Several huge cooling towers are shown.

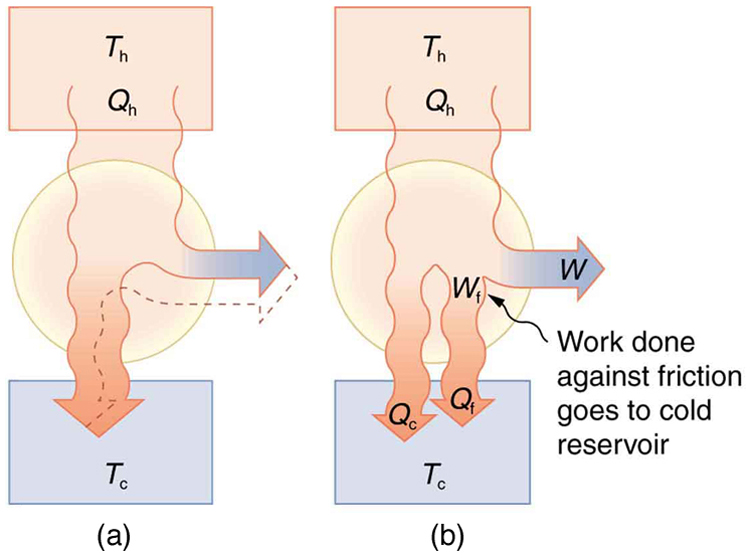
Since all real processes are irreversible, the actual efficiency of a heat engine can never be as great as that of a Carnot engine, as illustrated in (Figure)(a). Even with the best heat engine possible, there are always dissipative processes in peripheral equipment, such as electrical transformers or car transmissions. These further reduce the overall efficiency by converting some of the engine’s work output back into heat transfer, as shown in (Figure)(b).

Real heat engines are less efficient than Carnot engines. (a) Real engines use irreversible processes, reducing the heat transfer to work. Solid lines represent the actual process; the dashed lines are what a Carnot engine would do between the same two reservoirs. (b) Friction and other dissipative processes in the output mechanisms of a heat engine convert some of its work output into heat transfer to the environment.

Part a of the diagram shows a combustion engine represented as a circle to compare the efficiency of real and Carnot engines. The hot reservoir is a rectangular section above the circle shown at temperature T sub h. A cold reservoir is shown as a rectangular section below the circle at temperature T sub c. Heat Q sub h enters the heat engine as shown by a bold arrow. For a real engine a small part of it is shown to be expelled as output from the engine shown as a bold arrow leaving the circle and for a Carnot engine larger part of it is shown to leave as work shown by a dashed arrow leaving the circle. The remaining heat is shown to be returned back to the cold reservoir as shown by bold arrow toward it for real engines and comparatively lesser heat is given by the Carnot engine shown by a dashed arrow. Part b of the diagram shows an internal combustion engine represented as a circle to study friction and other dissipative processes in the output mechanisms of a heat engine. The hot reservoir is a rectangular section above the circle shown at temperature T sub h. A cold reservoir is shown as a rectangular section below the circle at temperature T sub c. Heat Q sub h enters the heat engine as shown by a bold arrow, work W is produced as output, shown leaving the system, and the remaining heat Q sub c and Q sub f are returned back to the cold reservoir as shown by bold arrows toward it. Q sub f is heat due to friction. The work done against friction goes as heat Q sub f to the cold reservoir.

Section Summary

  • The Carnot cycle is a theoretical cycle that is the most efficient cyclical process possible. Any engine using the Carnot cycle, which uses only reversible processes (adiabatic and isothermal), is known as a Carnot engine.
  • Any engine that uses the Carnot cycle enjoys the maximum theoretical efficiency.
  • While Carnot engines are ideal engines, in reality, no engine achieves Carnot’s theoretical maximum efficiency, since dissipative processes, such as friction, play a role. Carnot cycles without heat loss may be possible at absolute zero, but this has never been seen in nature.

Conceptual Questions

Think about the drinking bird at the beginning of this section ((Figure)). Although the bird enjoys the theoretical maximum efficiency possible, if left to its own devices over time, the bird will cease “drinking.” What are some of the dissipative processes that might cause the bird’s motion to cease?

Can improved engineering and materials be employed in heat engines to reduce heat transfer into the environment? Can they eliminate heat transfer into the environment entirely?

Does the second law of thermodynamics alter the conservation of energy principle?

Problem Exercises

A certain gasoline engine has an efficiency of 30.0%. What would the hot reservoir temperature be for a Carnot engine having that efficiency, if it operates with a cold reservoir temperature of \(2\text{00}\text{º}\text{C}\)?

\(\text{403}\text{º}\text{C}\)

A gas-cooled nuclear reactor operates between hot and cold reservoir temperatures of \(\text{700}\text{º}\text{C}\) and \(\text{27}\text{.}0\text{º}\text{C}\). (a) What is the maximum efficiency of a heat engine operating between these temperatures? (b) Find the ratio of this efficiency to the Carnot efficiency of a standard nuclear reactor (found in (Figure)).

(a) What is the hot reservoir temperature of a Carnot engine that has an efficiency of 42.0% and a cold reservoir temperature of \(\text{27}\text{.}0\text{º}\text{C}\)? (b) What must the hot reservoir temperature be for a real heat engine that achieves 0.700 of the maximum efficiency, but still has an efficiency of 42.0% (and a cold reservoir at \(\text{27}\text{.}0\text{º}\text{C}\))? (c) Does your answer imply practical limits to the efficiency of car gasoline engines?

(a) \(2\text{44}\text{º}\text{C}\)

(b) \(\text{477}\text{º}\text{C}\)

(c)Yes, since automobiles engines cannot get too hot without overheating, their efficiency is limited.

Steam locomotives have an efficiency of 17.0% and operate with a hot steam temperature of \(\text{425}\text{º}\text{C}\). (a) What would the cold reservoir temperature be if this were a Carnot engine? (b) What would the maximum efficiency of this steam engine be if its cold reservoir temperature were \(\text{150}\text{º}\text{C}\)?

Practical steam engines utilize \(\text{450}\text{º}\text{C}\) steam, which is later exhausted at \(\text{270}\text{º}\text{C}\). (a) What is the maximum efficiency that such a heat engine can have? (b) Since \(\text{270}\text{º}\text{C}\) steam is still quite hot, a second steam engine is sometimes operated using the exhaust of the first. What is the maximum efficiency of the second engine if its exhaust has a temperature of \(\text{150}\text{º}\text{C}\)? (c) What is the overall efficiency of the two engines? (d) Show that this is the same efficiency as a single Carnot engine operating between \(\text{450}\text{º}\text{C}\) and \(\text{150}\text{º}\text{C}\). Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.

(a) \({\mathit{\text{Eff}}}_{\text{1}}=1-\frac{{T}_{\text{c,1}}}{{T}_{\text{h,1}}}=1-\frac{\text{543 K}}{\text{723 K}}=0\text{.}\text{249}\phantom{\rule{0.25em}{0ex}}\text{or}\phantom{\rule{0.25em}{0ex}}\text{24}\text{.}9%\text{}\)

(b) \({\mathit{\text{Eff}}}_{2}=1-\frac{\text{423 K}}{\text{543 K}}=0\text{.}\text{221}\phantom{\rule{0.25em}{0ex}}\text{or}\phantom{\rule{0.25em}{0ex}}\text{22}\text{.}1%\text{}\)

(c) \(\begin{array}{l}{\mathit{\text{Eff}}}_{1}=1-\frac{{T}_{\text{c,1}}}{{T}_{\text{h,1}}}⇒{T}_{\text{c,1}}={T}_{\text{h,1}}\left(1,-,{\mathit{\text{eff}}}_{1}\right)\end{array}\) \(\begin{array}{l}\text{similarly,}\phantom{\rule{0.25em}{0ex}}{T}_{\text{c,2}}={T}_{\text{h,2}}\left(1-{\mathit{\text{Eff}}}_{2}\right)\end{array}\) \(\begin{array}{l}\text{using}\phantom{\rule{0.25em}{0ex}}{T}_{\text{h,2}}={T}_{\text{c,1}}\phantom{\rule{0.25em}{0ex}}\text{in}\phantom{\rule{0.25em}{0ex}}\text{above}\phantom{\rule{0.25em}{0ex}}\text{equation}\phantom{\rule{0.25em}{0ex}}\text{gives}\end{array}\) \(\begin{array}{l}{T}_{\text{c,2}}={T}_{\text{h,1}}\left(1-{\mathit{\text{Eff}}}_{1}\right)\left(1-{\mathit{\text{Eff}}}_{2}\right)\equiv {T}_{\text{h,1}}\left(1-{\mathrm{Eff}}_{\text{overall}}\right)\\ \therefore \left(1-{\mathrm{Eff}}_{\text{overall}}\right)=\left(1-{\mathit{\text{Eff}}}_{1}\right)\left(1-{\mathit{\text{Eff}}}_{2}\right)\\ {\mathrm{Eff}}_{\text{overall}}=1-\left(1-0\text{.}\text{249}\right)\left(1-0\text{.}\text{221}\right)=\text{41}\text{.}5%\text{}\end{array}\)

(d) \({\text{Eff}}_{\text{overall}}=1-\frac{\text{423 K}}{\text{723 K}}=0\text{.}\text{415}\phantom{\rule{0.25em}{0ex}}\text{or}\phantom{\rule{0.25em}{0ex}}\text{41}\text{.}5%\text{}\)

A coal-fired electrical power station has an efficiency of 38%. The temperature of the steam leaving the boiler is \(\text{550}\text{º}\text{C}\). What percentage of the maximum efficiency does this station obtain? (Assume the temperature of the environment is \(\text{20}\text{º}\text{C}\).)

Would you be willing to financially back an inventor who is marketing a device that she claims has 25 kJ of heat transfer at 600 K, has heat transfer to the environment at 300 K, and does 12 kJ of work? Explain your answer.

The heat transfer to the cold reservoir is \({Q}_{\text{c}}={Q}_{\text{h}}-W=\text{25}\phantom{\rule{0.25em}{0ex}}\text{kJ}-\text{12}\phantom{\rule{0.25em}{0ex}}\text{kJ}=\text{13}\phantom{\rule{0.25em}{0ex}}\text{kJ}\), so the efficiency is \(\mathit{Eff}=1-\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}=1-\frac{\text{13}\phantom{\rule{0.25em}{0ex}}\text{kJ}}{\text{25}\phantom{\rule{0.25em}{0ex}}\text{kJ}}=0\text{.}\text{48}\). The Carnot efficiency is \({\mathit{\text{Eff}}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}=1-\frac{\text{300}\phantom{\rule{0.25em}{0ex}}\text{K}}{\text{600}\phantom{\rule{0.25em}{0ex}}\text{K}}=0\text{.}\text{50}\). The actual efficiency is 96% of the Carnot efficiency, which is much higher than the best-ever achieved of about 70%, so her scheme is likely to be fraudulent.

Unreasonable Results

(a) Suppose you want to design a steam engine that has heat transfer to the environment at \(\text{270ºC}\) and has a Carnot efficiency of 0.800. What temperature of hot steam must you use? (b) What is unreasonable about the temperature? (c) Which premise is unreasonable?

Unreasonable Results

Calculate the cold reservoir temperature of a steam engine that uses hot steam at \(\text{450}\text{º}\text{C}\) and has a Carnot efficiency of 0.700. (b) What is unreasonable about the temperature? (c) Which premise is unreasonable?

(a) \(\text{–56.3ºC}\)

(b) The temperature is too cold for the output of a steam engine (the local environment). It is below the freezing point of water.

(c) The assumed efficiency is too high.

Glossary

Carnot cycle
a cyclical process that uses only reversible processes, the adiabatic and isothermal processes
Carnot engine
a heat engine that uses a Carnot cycle
Carnot efficiency
the maximum theoretical efficiency for a heat engine

License

Icon for the Creative Commons Attribution 4.0 International License

Intro to Physics for Non-Majors Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book