8
Click play on the following audio player to listen along as you read this section.
https://media.bccampus.ca/id/0_b0vcflny?width=608&height=50&playerId=23449753

So far we’ve determined that pressure is a force per unit area and that pressure can be stated in different ways with pounds per square inch being the most common. We calculated the pressure at the base of an object or piping system filled with water.
Now it’s time to calculate the total force at the base of an object or piping system given the pressure exerted at its base. As before we will use water as the fluid in the example questions.
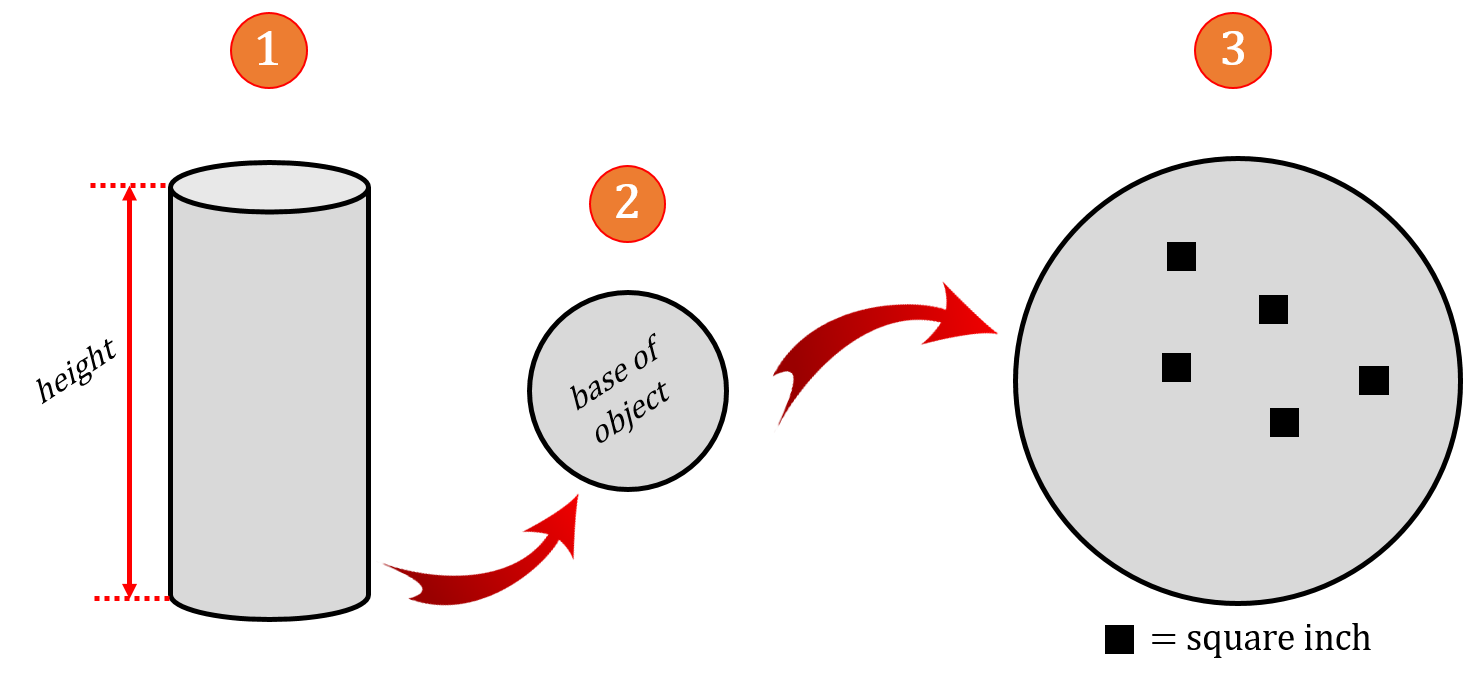
Take a look at the figure below and then read the explanation below that.

Start with an object filled with water. In this case a cylinder or possibly something like a hot water tank. The object will be three dimensional and have a height, width and depth.

This is the base of the object. As we are calculating total force at the base of this object we have to decide what the base consists of and define its parameters.

The base has been expanded for visual purposes to allow for the introduction of a few square inches inserted into the base. As stated previously we are calculating pressure in pounds per square inch therefore it’s going to be important to find the area at the base in square inches.

After all that we can put everything together to get our total force formula.
[latex]\text{total force} = \text{ area} \times \text{ psi}[/latex]

There are a couple things to note here.
1) The area must be in square inches
2) The height used to determine psi must be in feet.
This concept occasionally mixes people up as one part of the equation is calculated using inches and the other part is calculated using feet. This is generally opposite from what we’ve been saying in most of this math journey where we’ve made sure all the variables must be in the same unit. Let’s head off to an example to put all this together.
Example
Calculate the force at the base of the tank pictured above. Assume that the tank is filled with water.
Step 1: Write down the formula you’ll be working with.
Note that in this case we have a rectangular tank with the area of the base being the length multiplied by the width.
[latex]\text{total force} = (l \times w) \times (height \times 0.433)[/latex]
Step 2: Write down the variables and put them in proper units to work with.
Step 3: Plug the reworked variables into the equation.
[latex]\begin{array}{c} \text{total force} &= (l \times w) \times (height \times 0.433) \\ \text{total force} &= (32in \times 8 in) \times (1.08 ft \times 0.433 \text{ psi/ft}) \\ \text{total force} &= (256 in^2) \times (0.464 \text{ psi}) \\ \text{total force} &= 118.78 \text{ pounds} \end{array}[/latex]
[latex]118.78 lbs[/latex]
Note the units that we end up with. We end up with pounds as our total force. The inches in the area at the base and the inches in the pounds per square inch cancel each other out. This leaves us with just pounds as an answer.
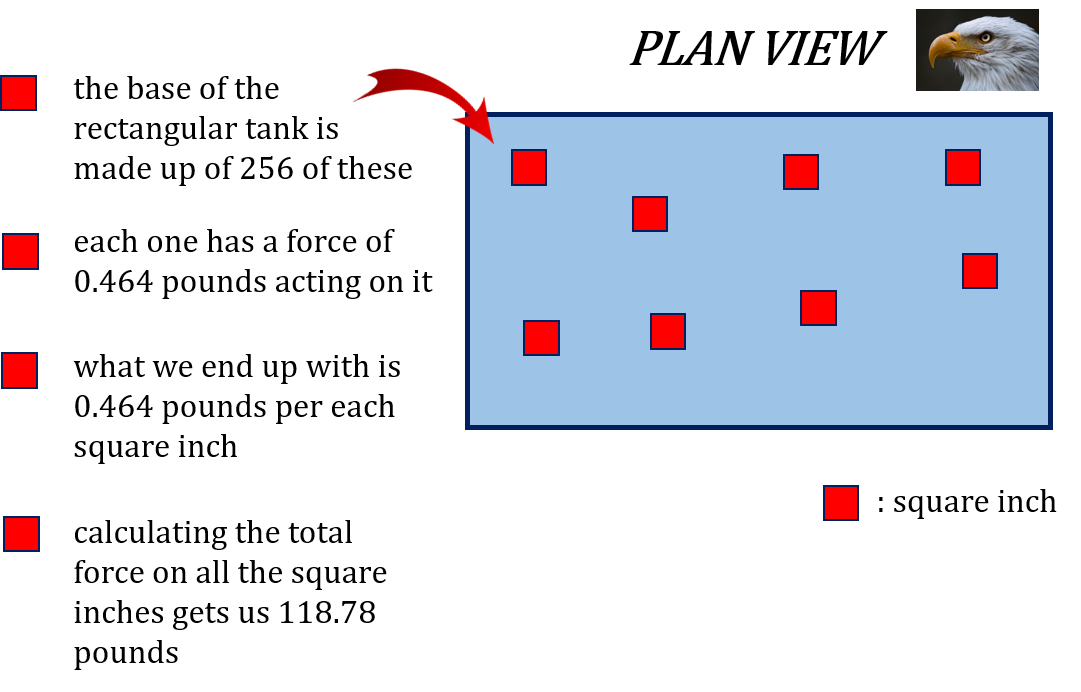
The total force at the base of the tank works out to be 188.78 pounds. There are 256 square inches at the base and each square inch has 0.464 pounds of force acting on it. Take a look at the plan view below for a better understanding.
Question: What is a plan view?
Answer: A plan view is when you look at an object from above. It’s as if you had a bird’s eye view of an object.

Here’s another scenario but this time we’ll switch things up a little. Say we have a piping system filled with water which is pressurised by a pump. We’ll add a gate valve into the system. This valve is closed and holding water back from one side of the system.
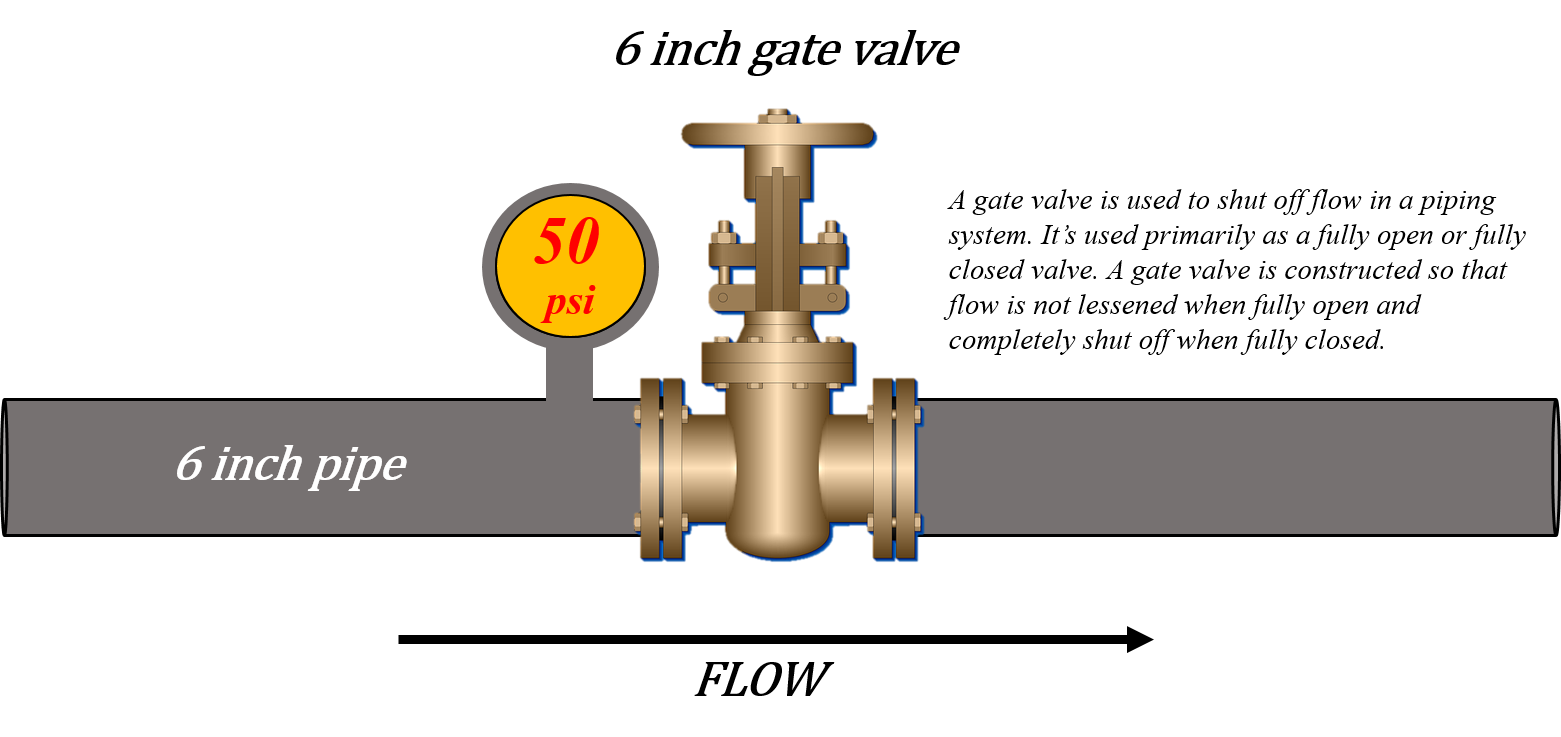
The system has been pressurized to 50 psi. Note in this example the height of the system does not matter like it did in the previous example. We don’t have to calculate psi as it is given to us. What we are required to find out is how much force is acting upon the gate valve.
Now as before we would use the same formula which requires psi and area. For our example we’ll say that we have a six inch gate valve. What we have is 50 psi acting on a 6 inch gate valve. What is the total force acting on the gate valve?
Step 1: Write down the formula you are going to work with.
[latex]\text{total force} = \text{ area} \times \text{psi}[/latex]
Here is the formula for area of a circle.
[latex]\text{area} = \pi \times r^2[/latex]
We could then rewrite the formula.
[latex]\text{total force} = (\pi \times r^2) \times \text{psi}[/latex]
Step 2: Insert the variables into the equation making sure that theyare in the correct units.
[latex]\begin{array}{c} \text{total force} &= (\pi \times r^2) \times \text{ psi} \\ &= (\pi \times 3^2) \times 50 \\ &= 28.26 \times 50 \\ &= 1413 \text{ pounds}\end{array}[/latex]
There you have it. The total force acting upon the gate valve is 1,413 pounds given that it’s a six inch gate valve and has 50 psi acting upon it.
Give the following practice questions a try. Make sure to check out the video answer which goes along with the question once you have completed the question.
Practice Questions
Question 1

Haiko installs gravity fed water systems which are a water source for either a single home or a number of homes in a small area. The gravity fed tank is 72 feet above the house and the water is supplied by a 1 1/2 inch pipe. What is the pressure available at the house?
https://media.bccampus.ca/id/0_h477csix?width=608&height=402&playerId=23449753
Question 2

Rolf is a Swiss born sprinkler fitter installing a new sprinkler system in an old run down warehouse now being used as a compostable coffee pod manufacturer. They will hopefully have the capability to make 50 million compostable coffee pods by the middle of next year.
The sprinkler system has to be tested to 50 psi above the maximum pressure for about 2 hours. In this case the maximum pressure is 120 psi. The piping is all going to be 4 inch and there is a gate valve at the end of the system preventing water from getting into an unfinished part of the system. Calculate the total force acting on that gate valve.
https://media.bccampus.ca/id/0_5cp7uu9e?width=608&height=402&playerId=23449753
Image Descriptions
Figure 8.1: Showing the plan view of an object. The plan view is represented by a blue rectangle and red blocks indicate each square inch of the blue rectangle.
- The base of the rectangular tank is made up of 256 of these [red blocks].
- Each one has a force of 0.464 pounds acting on it.
- What we end up with is 0.464 pounds per each square inch.
- Calculating the total force on all the square inches gets us 118.78 pounds. [Return to image]
Figure 8.2: A gate valve is used to shut off flow in a piping system. It’s used primarily as a fully open or fully closed valve. A gate valve is constructed so that flow is not lessened when fully open and completely shut off when fully closed. Pictured is a 6 inch gate valve with 50 pounds per square inch acting on it. The pipe is 6 inches. The flow is left to right. [Return to image]