1
Click play on the following audio player to listen along as you read this section.
https://media.bccampus.ca/id/0_jtog7ybp?width=608&height=50&playerId=23449753

In the previous chapter we took a look at volume, what it is and how to calculate it. When dealing with volume we ended up working with units such as cubic feet, cubic inches or cubic meters.
Let’s quickly revisit the definition of volume: Volume is the space which takes up a three dimensional object.
What if I was to talk about volume but using the term capacity instead? Would that change your idea of what volume looks like? What does the term capacity bring to mind when you hear the word?
Capacity is often referred to as the largest amount of something (possibly a solid, liquid or gas) that can be held or contained in a specific volume. You might be thinking that you’ve heard capacity mentioned in other ways such as the amount of people that can fit into a stadium or large venue. You would be correct.

An example would be the capacity of the University of Michigan football team stadium. It was built in 1926 and has a capacity of 107,601 people. You heard that right. It holds over 100,000 people. Crazy! In this case we would use the term capacity to describe the number of people that can fit into the stadium. The stadium is also referred to as “The Big House” for obvious reasons. Although this is not the type of capacity we will be dealing with it’s still a pretty cool ex
![]()
ample of another version of capacity.
I’m going to leave it there regarding the difference between volume and capacity but if you would like to learn more check out the following website: Differences Between Volume and Capacity

If you were asked to find the capacity of the gas can to the left what type of units would you be using to give your answer?
For many of us the first thing that might come to mind would be the term gallon or litre and as it turns out these are the exact terms we use when describing capacities. We’ll start with gallons.
Gallons

When you think of gallons what is the first thing that comes to mind? For me its either gasoline that goes into a car or maybe milk. The funny thing about that is we actually measure both of these things in litres here in Canada. Whatever the case I still think of putting gallons of gas into my car rather than litres although in the future I might not be thinking of putting either gallons or litres as we might all be headed towards electric vehicles anyway.
Let’s break it down even further. Are you aware that gallons can be expressed two different ways? There is the imperial Gallon and the U.S. gallon. Here in Canada we generally deal with imperial gallons but as we also deal with the United States when it comes to products such as hot water tanks and boilers we should also be familiar with the U.S. gallon.
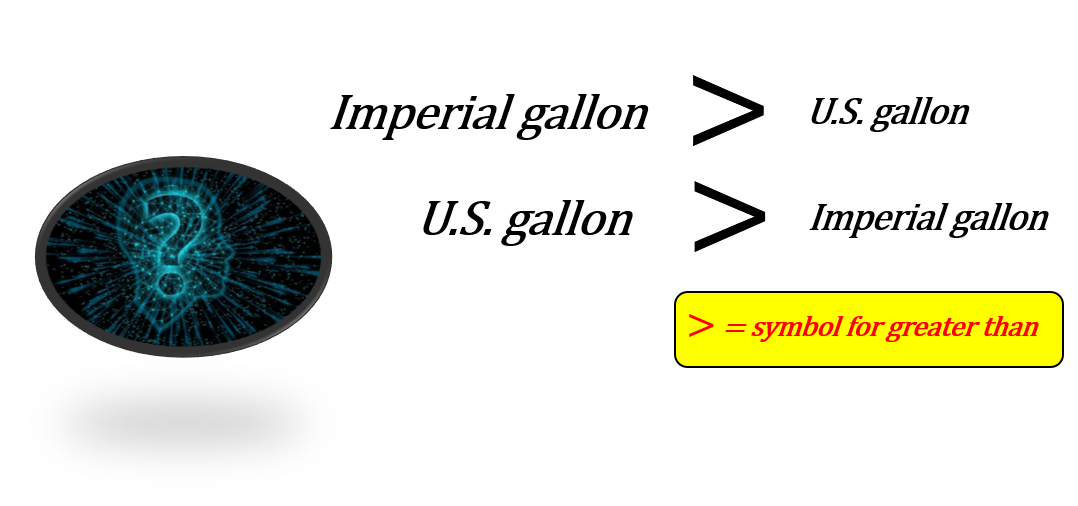
Question: Which do you think is bigger, the imperial gallon or the U.S. gallon?
Answer: We’ll answer that in the last part of this section. If you’re curious and can’t wait until the end and want to dive ahead then maybe take a look online and see if you can find the answer.

The imperial gallon story originates in jolly ‘ole England. The English Weights and Measures Act came into being during the 1800’s which made the British Imperial System the go to place for defining units. As a result the imperial gallon replaced the wine, ale and corn gallons then in use.
Maybe the first thing we should do is try and visualize the size of an imperial gallon. If we are going to do that we should have a reference or starting point.
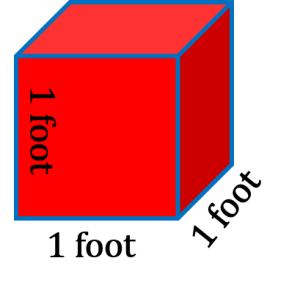
Let’s go back to the cubic foot that we talked about in the last chapter. Remember that a cubic foot has 3 dimensions and we referred to it in terms of volume. Its one foot by one foot by one foot.
As an imperial gallon refers to capacity it is referring to an amount of stuff. For our purposes that stuff can be either a solid, liquid or a gas. The question then becomes “how many imperial gallons does it take to fill up a cubic foot?”
Wait a minute? Maybe it’s the other way around. Maybe an imperial gallon contains so much stuff that putting it into a cubic foot will overflow the cubic foot?
Any guesses on which can hold more stuff?

Check out the answer below.

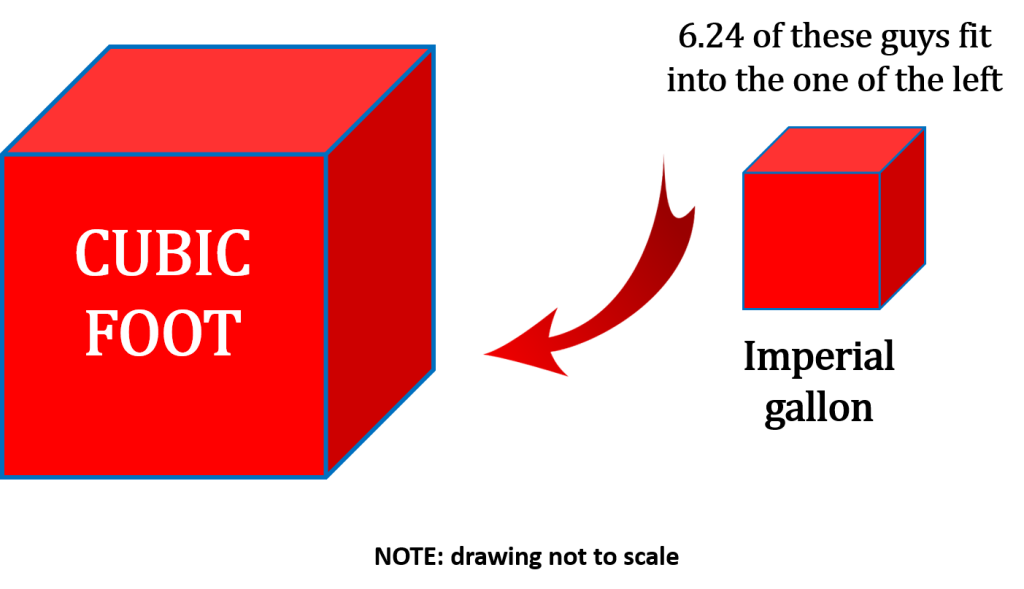
As it turns out a cubic foot is quite a bit larger than an imperial gallon. In fact it’s 6.24 times larger meaning that you can fit 6.24 imperial gallons into a cubic foot.
This leads up to our first capacity translation.
Now we can get the volume of a cubic foot and translate that into imperial gallons.
Let’s try an example.
Example

Let’s create a question which not only involves cubic feet and imperial gallons but which also involves a little math from the previous chapters.
A swimming pool is 30 feet long, 15 feet wide and 4 feet deep. How many imperial gallons does the pool hold?
(Note: I’m going to have to write a lot of math books before I can afford that place on the left)
Step 1: Organize your thoughts. Figure out what the question is asking and what direction you want to take to get there. What you’ll need to do first is calculate the volume in cubic feet given the dimension of the pool.
Step 2: Write down the formula for calculating volume and then calculate the volume.
[latex]\begin{equation}\begin{split} \text{Volume} &= \text{length} \times \text{width} \times \text{height} \\ &= 30 \text{ feet} \times 15 \text{ feet} \times 4 \text{ feet} \\ &= 1800 ft^3 \end{split}\end{equation}[/latex]
We’ve established that the volume of the pool is 1800 cubic feet. We also know the relationship between cubic feet and imperial gallons. Therefore we should be able to calculate the capacity of the pool in imperial gallons.
[latex]1 \text{ cubic foot} = 6.24 \text{ imperial gallons}[/latex]
Step 3: Work this into an equation using the cross multiplying technique.
[latex]\dfrac{1 \text{ cubic foot}}{1800 \text{ cubic feet}} = \dfrac{6.24 \text{ imperial gallons}}{\text{X imperial gallons}}[/latex]
[latex]\begin{array}{c}1 \times \text{ X} = 1800 \times 6.24 \\ \text{X} = 11,232 \end{array}[/latex]
[latex]\text{answer} = 11,232 \text{ imperial gallons}[/latex]

Now let’s move on to the U.S. gallon. We’ll use the same logic when dealing with a U.S. gallon as we did when we were dealing with the imperial gallon.
How about a little history first. Back in 1776 the American Colonies decided it was time to become independent of the British Empire and the United States was born. Okay, that might have been a bit of a simplistic summary but you get the idea. The newly formed United States decided to adopt the Queen Ann gallon. Queen Anne ruled England around 1706 and during this time the wine gallon became the standard measurement for a gallon. A wine gallon was 231 cubic inches which works out to approximately 3.78 liters (remember those two numbers as they could come in handy later). Essentially this was the standard used in England when America revolted and became its own country.
Let’s starting talking about the capacity of a U.S. gallon. Once again we’ll use a cubic foot as our standard.
Question: “Do you think that if you poured one U.S. gallon into a cubic foot it would fill up the cubic foot to the point where it overflowed or do you think you would need more than one U.S. gallon to fill up a cubic foot?”
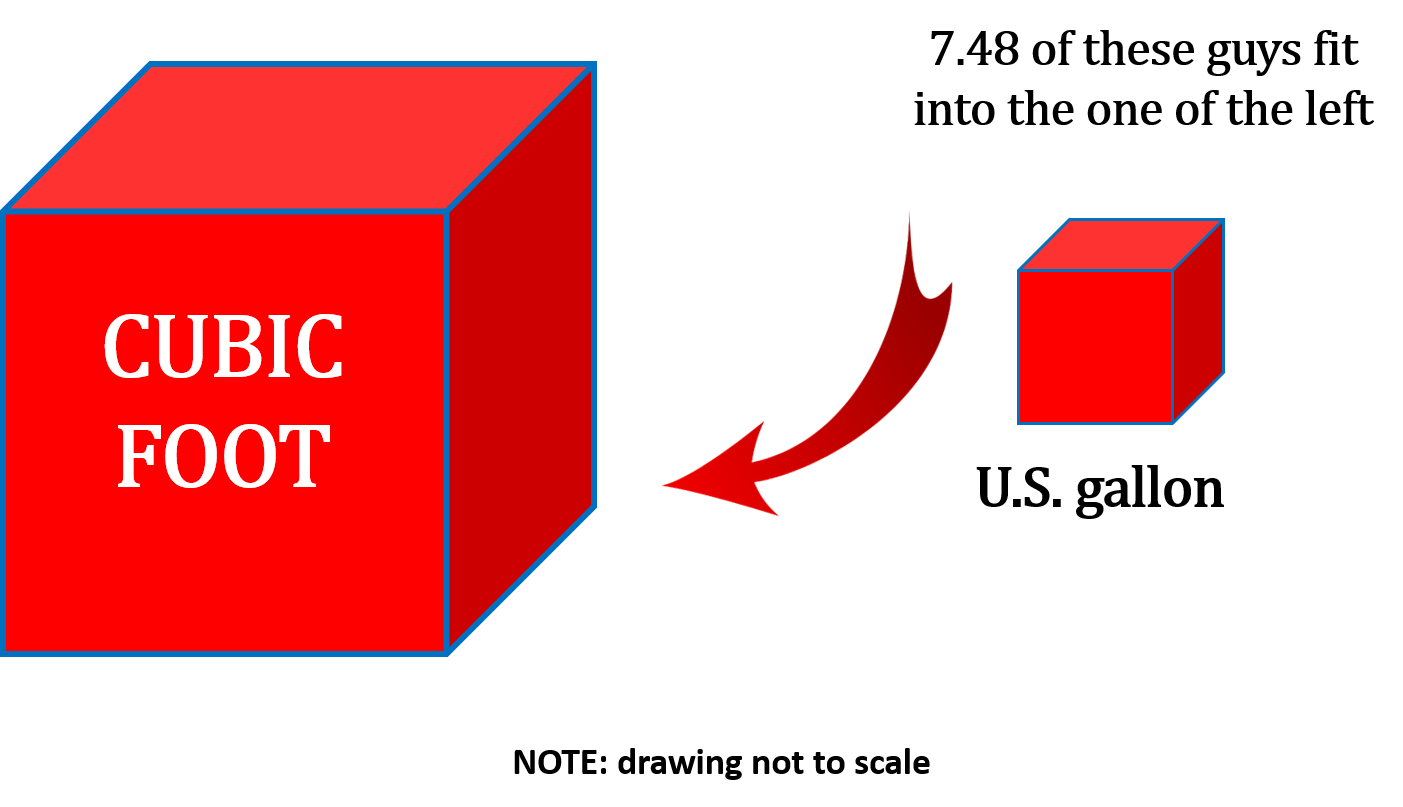
Maybe we should reference an imperial gallon here. Remember that it took 6.24 imperial gallons to fill up a cubic foot. I would think that although an imperial gallon and a U.S. gallon are most likely different they are probably somewhat close in size as they are both gallons. From this assumption I would conclude that a U.S. gallon (like an imperial gallon) is smaller than a cubic foot.
This leads up to our second capacity translation:
Now we can calculate volume in cubic feet and translate that into U.S. gallons.
Let’s try an example.
Example

The Amazon River in South America is the largest river in the world in regards to discharge by volume. The volume (or flow) of the Amazon is 209,027 cubic meters per second. Yes you read that correctly. That’s per second!!!
How many U.S. gallons per second flows in the Amazon?
Step 1: As our U.S. gallon capacity translation deals with cubic feet and not cubic meters our first step it to change the cubic meters into cubic feet. For that we need to go back a chapter or two and find the number which translates cubic meters into cubic feet.
[latex]1 \text{cubic meter} = 35.31 \text{cubic feet}[/latex]
Step 2: Change the cubic meters into cubic feet. Once again we cross multiply.
[latex]\dfrac{1 \text{ cubic foot}}{209,207 \text{ cubic meters}} = \dfrac{35.31 \text{ cubic feet}}{\text{X cubic feet}}[/latex]
[latex]\begin{array}{c} 1 \times \text{ X} &= 209,207 \times 35.31 \\ \text{X} &= 7387,099.17 \end{array}[/latex]
[latex]\text{answer} = 7,387,099.17 \text{ imperial gallons}[/latex]
Step 3: Convert the cubic feet into U.S. gallons remembering that 1 cubic foot contains 7.48 U.S. gallons.
[latex]\dfrac{1 \text{ cubic foot}}{7,387,099.17 \text{ cubic feet}} = \dfrac{7.48 \text{ U.S. gallons}}{\text{X US. gallons}}[/latex]
[latex]\begin{array}{c}1 \times \text{ X} = 7,387,099.17 \times 7.48 \\ \text{X} = 55,255,501.8 \end{array}[/latex]
[latex]\text{answer} = 55,255,501.8 \text{ imperial gallons}[/latex]
Remember the question we asked in the first part of this section?
Question: Do you think an imperial gallon is bigger than a U.S. gallon or do you think a U.S. gallon is bigger than an imperial gallon?
Before we answer the question why don’t we put the two capacity translations back up.
[latex]1 \text{ cubic foot} = 6.24 \text{ imperial gallons}[/latex]
[latex]1 \text{ cubic foot} = 7.48 \text{ U.S. gallons}[/latex]
The natural instinct, or maybe we should say logic, seems to be that since 7.48 is larger than 6.24 then it would make sense that the U.S. gallon is bigger.
In fact it’s the other way around. You would require 6.24 imperial gallons in order to fill up a cubic foot. You would need more than that (7.48) when dealing with U.S. gallons. If it takes more U.S. gallons then each of those U.S. gallons must not be as big as an imperial gallon.
And in fact this is the case. An imperial gallon is about 20% bigger than a U.S. gallon. That why in the end of the day it takes more U.S. gallons to fill up a cubic foot.
Let’s take it one step further and do the math.
If we say that the imperial gallon is 20% larger than a U.S. gallon then it would make sense that:
[latex]\text{U.S. gallon} + 20\% = \text{ imperial gallon}[/latex]

So how do we prove that?
I guess the easiest way might be to convert gallons back into cubic feet and then compare the numbers.
Let’s start with imperial gallons.
[latex]\dfrac{1 \text{ cubic foot}}{X \text{ cubic feet}} = \dfrac{6.24 \text{ imperial gallons}}{1 \text{ imperial gallon}}[/latex]
[latex]\begin{array}{c} 1 \times \text 1 = X \times 6.24 \\ \text{X} = \dfrac{1}{6.24} \\ \text{X} = 0.160\end{array}[/latex]
[latex]\text{answer} = 0.160 \text{ cubic feet}[/latex]
Now let’s convert the U.S. gallons into cubic feet.
[latex]\dfrac{1 \text{ cubic foot}}{X \text{ cubic feet}} = \dfrac{7.48 \text{ U.S. gallons}}{1 \text{ U.S. gallon}}[/latex]
[latex]\begin{array}{c} 1 \times \text 1 = X \times 7.48 \\ \text{X} = \dfrac{1}{7.48} \\ \text{X} = 0.133\end{array}[/latex]
[latex]\text{answer} = 0.133 \text{ cubic feet}[/latex]
If we were to continue with the math we would say that:
[latex]\text{U.S. gallons }+ 20\% = \text{ imperial gallons}[/latex]
or
[latex]\begin{array}{c} \text{U.S. gallons } \times 1.2 &= \text{ imperial gallons} \\ 0.133 \times 1.2 &= 0.160 \end{array}[/latex]

Now go and plug the numbers into your calculator just to confirm.
As you see it turns out to be true. You might not get exactly 0.160 but that is just due to a little rounding here and there.
What we proved is that an imperial gallon is indeed 20% larger than a U.S. gallon.
We could have also done this mathematical trick:
[latex]6.24 \times 1.2 = 7.48[/latex]

The guy to the left is Hanford. He’s wondering why I went through all that math to make a relatively simple point.
Well it’s because learning to understand math from a conceptual level and being able to prove that concept will help you grasp math at much more of a fundamental level. If you can wrap your head around these concepts and truly understand them rather than memorizing them then math not only makes a lot more sense but it becomes more enjoyable.
Hanford: “I can see that. The more I understand where numbers are derived from and the more I understand math conceptually the easier it seems to become for me. I’m memorizing less and applying more.”

In a sense it’s like the trades. Let’s take the automotive trade as an example. It’s one thing to learn how to drive a car and remember all the different aspects of driving but it takes it to a whole other level when you can get under the hood and begin to understand what is actually happening when the car is in operation.
Add to that the ability to fix any issues that come up takes it another level.
The same thing can be applied to math. It’s one thing to memorize a formula and add numbers to it but it’s a whole other level when you can conceptualize the formula and really understand where it comes from.
Alright that’s enough of the logic talk. Why don’t you try a couple of practice questions. Make sure to check out the video answers once you are done.
Practice Questions
Question 1

The barrels to the left are used for making red wine in the Okanagan region of southern British Columbia. That region of the province is known for its warm, dry climate and great for growing the grapes used for making wine.
Aldo is a Sommelier and is calculating how much wine all the barrels in the picture to the left can hold. In case you were curious a wine sommelier is a person who is a trained and knowledgeable wine professional. He has been told that each barrel has a volume of 9.65 cubic feet. Calculate the total number of imperial gallons of wine in all the barrels.
https://media.bccampus.ca/id/0_50fdrqrw?width=608&height=402&playerId=23449753
![]() If you want to know more about sommeliers check out the following link: Sommelier.
If you want to know more about sommeliers check out the following link: Sommelier.
Question 2

A high rise building is under construction in the heart of Vancouver. The carpentry and steel trades are working together to create concrete support columns in the building. There are a total of 14 support columns. Each column is 2 feet by 2 feet by 10 feet. Normally concrete is ordered in cubic yards but we’re going to mix it up a bit here and put our order in U.S. gallons.
How many U.S. gallons of concrete would we have to order to fill up all 14 of the columns?
https://media.bccampus.ca/id/0_5asidyuw?width=608&height=402&playerId=23449753
![]() If you want to know more about ordering concrete click the following link: How to Estimate a Concrete Order.
If you want to know more about ordering concrete click the following link: How to Estimate a Concrete Order.