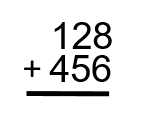7 Adding Whole Numbers
Harpreet and Jamieson are currently working a job that requires seven toilets to be installed in one area of the building and six toilets in another. In total, they need to install 13 toilets.
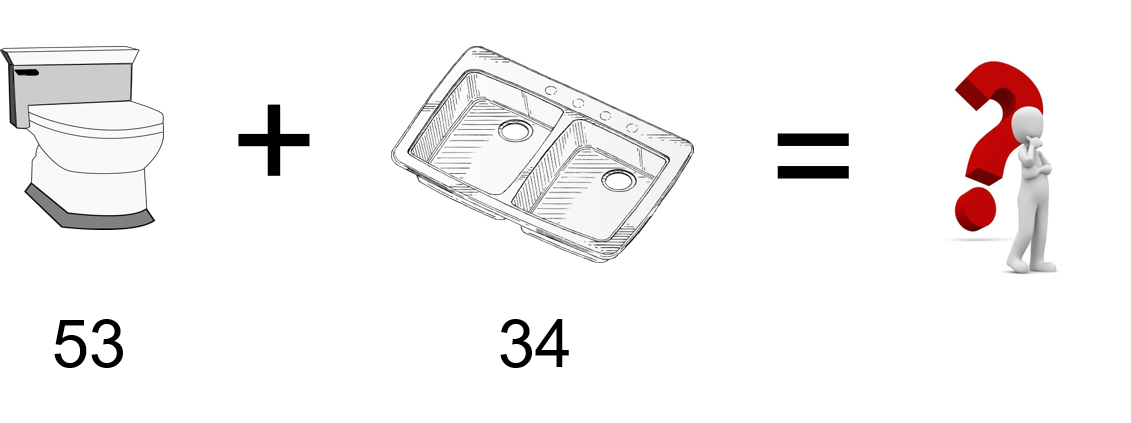
Now, that might not be too hard to do in our heads, but what if we need to add larger numbers? For instance, a job that they are bidding on has 53 toilets and 34 kitchen sinks. That might be harder to add in your head.
An easy way to add is to use a calculator, and if we did, we would get an answer of 87. But learning to add these two whole numbers using math principles can help us not only add the numbers, but also visualize how these numbers go together.
Let’s go back to the place value system to help us out:
First, look at 53, which has 5 tens and 3 ones.
Then, look at 34, which has 3 tens and 4 ones.
Add the tens up: 5 tens + 3 tens = 8 tens.
Add the ones up: 3 ones + 4 ones = 7 ones.
When we put the original numbers in the place value system and add, we get a total of 87. Separating this number into each of its digits and positioning them in the place value system can help us visualize the value of each of the digits.
Follow the steps outlined below to see how this process looks mathematically.
Example
We’ll use the same numbers from the previous example:
Step 1: Put the question into a formula that is easy to work with.
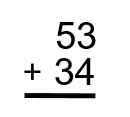Step 2: Add up the ones. In this case, we have 3 and 4. Together, they add up to 7.
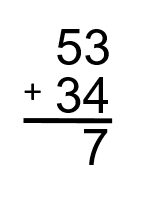Step 3: Add up the tens. In this case, we have 5 and 3. Together, they add up to 8.
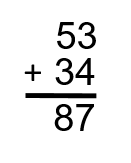
That example worked out well, as neither the ones nor the tens added up to more than 9. But what if they did? Take a look at the next example to see how this works.
The word “sum” is math language for adding numbers together. When we say, “What is the sum of 27 and 45?” what we are saying is, “What is the total of those numbers if we added them together?”
Example
Find the sum of 27 and 45.
To get the sum of these numbers, we will go back to our three steps.
Step 1: Put the question into a formula that is easy to work with.
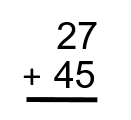
Step 2: Add up the ones. In this case, we have 7 and 5. Together, they add up to 12. This is where we do what is called “carrying the one.” Take a look at the following image to see this in action:
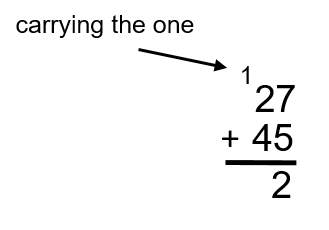
Note: In this case, we do not put the number 12 at the bottom of the equation. Instead, we “carry the one” into the next spot (the tens) in the place value system.
Step 3: Add up the tens. In this case, we have 2 and 4. Together, they add up to 6. We also have to take into account the one that we carried over. We add that in as well to get a total of 7 in the tens place.
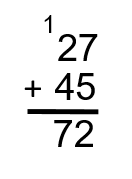
Note: If it turned out that the tens added up to more than 9, we could carry the one again into the hundreds column. Take a look below to see how this works.
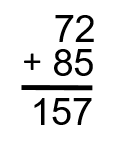
As there are no other values in the hundreds column in this question, we just go ahead and place the one in the hundreds column.
Practice Questions
Try a couple practice questions yourself and check the video answers to see how you did. Make sure to follow the steps outlined above and think about the place value of each of the digits.
Question 1
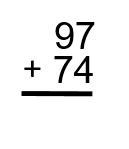
Question 2
