3 Multiplying Fractions

The following equation is an example of multiplying fractions. At first glance, it might look harder than either adding or subtracting fractions, but in reality, it’s much easier. What might be tougher to understand is the answer that you get when you multiply fractions.
[latex]\LARGE\dfrac{1}{4}\times\dfrac{1}{2}=?[/latex]
We’ll take a look at this visually, using a circle cut into parts to work this out. To start, we’ll divide the circle into 4 equal parts. One of those parts would equal one-quarter of the circle.
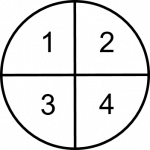
If we were to multiply that ¼ by ½, what we would be doing mathematically is taking ½ of the ¼ piece, or essentially splitting that ¼ into two equal parts. That would end up representing ⅛ of the circle.
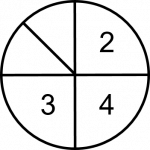
Mathematically, it’s done like this:
Multiply the numerators together
[latex]1\times1=1[/latex]
AND
Multiply the denominators together
[latex]2\times4=8[/latex]
What we end up with is this:
[latex]\LARGE\dfrac{1}{2}\times\dfrac{1}{4}=\dfrac{1}{8}[/latex]
Example
Let’s go back to Abigail, Hanna, and Naomi. They’ve now completed another level of their schooling and are getting to the end of their apprenticeships. All three are working on the same job, which is a three-storey wood-frame building, and each is responsible for roughing-in 30 suites. They are required to wire ⅙ of those suites every week. One week, Hanna had to miss two days. Therefore, she only worked 3 out of the 5 days, or ⅗ of the time. What fraction of suites would she have been able to rough-in that week, taking into consideration her time away?
Start by writing down the fractions we are going to work with in this situation.
[latex]\dfrac{1}{6}\text{ The amount of suites needed to be completed during a 5-day work week.}[/latex]
[latex]\dfrac{3}{5}\text{ The fraction of time worked during the week, 3 out of 5 days.}[/latex]
Then multiply the two fractions together, sticking to our formula of multiplying the numerators together and then multiplying the denominators together.
[latex]\LARGE\text{numerators }1\times3=3[/latex]
[latex]\LARGE\text{denominators }6\times5=30[/latex]
And that makes the answer:
[latex]\LARGE\dfrac{1}{6}\times\dfrac{3}{5}=\dfrac{3}{30}[/latex]
Which can then be reduced to its lowest terms:
[latex]\LARGE\dfrac{3}{30}\rightarrow\dfrac{1}{10}[/latex]
Here is another example. Let’s go through the steps in this one.
Example
[latex]\LARGE\dfrac{5}{8}\times\dfrac{3}{4}=?[/latex]
Step 1: Multiply the numerators together.
[latex]\LARGE5\times3=15[/latex]
Step 2: Multiply the denominators together.
[latex]\LARGE8\times4=32[/latex]
Step 3: Put each of the answers in the appropriate place in the fraction.
[latex]\LARGE\dfrac{5}{8}\times\dfrac{3}{4}=\dfrac{15}{32}[/latex]
Step 4: Put the answer in lowest terms, if necessary, and change to a mixed number, if necessary. In this question, we are good on both accounts.
[latex]\LARGE\text{Final answer }=\dfrac{15}{32}[/latex]
Up to this point, you may have been thinking that you got this and this is easy, but now, let’s step up the difficulty level a bit.
Example
[latex]\LARGE4\dfrac{2}{5}\times2\dfrac{1}{4}=?[/latex]
Before you start, do you see a problem? The problem is that you are now trying to multiply two mixed numbers together. How does that work? Can you just go ahead and try to multiply them as they are? The answer is NO, but the solution to the problem is not that difficult: you just have to take one extra step before going through the process.
The first thing you have to do is change each of the mixed numbers into improper fractions. From that point on, the process is the same.
Step 1: Change each of the mixed numbers into improper fractions. This is the only way to answer this question. You cannot multiply the numbers in the state they are in.
[latex]\LARGE4\dfrac{2}{5}=\dfrac{22}{5}[/latex]
(5 × 4 + 2 = 22)
[latex]\LARGE2\dfrac{1}{4}=\dfrac{9}{4}[/latex]
(4 × 2 + 1 = 9)
Step 2: Multiply the numerators together.
[latex]\LARGE22\times9=198[/latex]
Step 3: Multiply the denominators together.
[latex]\LARGE5\times4=20[/latex]
Step 4: Put each of the answers in the appropriate place in the fraction.
[latex]\LARGE\dfrac{22}{5}\times\dfrac{9}{4}=\dfrac{198}{20}[/latex]
Step 5: Put the answer in lowest terms, if necessary, and change to a mixed number, if necessary. In this case, we have to do both. We’ll start by putting the fraction into lowest terms.
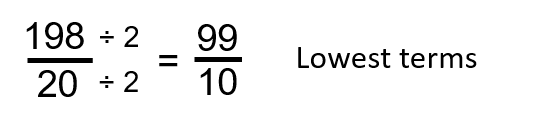
Then take that and put it into a mixed number.
[latex]\LARGE\dfrac{99}{10}=9\dfrac{9}{10}\text{ Mixed number}[/latex]
Practice Questions
Try a couple questions yourself. Make sure to put your answer into lowest terms and, if necessary, turn it back into a mixed number. Check the video answers when you are done to see if you are on the right track.
Question 1
[latex]\LARGE\dfrac{4}{7}\times\dfrac{3}{8}=[/latex]
https://video.bccampus.ca/id/0_102s3rf3?width=608&height=402&playerId=23448552
Question 2
[latex]\LARGE\dfrac{6}{11}\times\dfrac{5}{9}=[/latex]
https://video.bccampus.ca/id/0_uwfhiu9a?width=608&height=402&playerId=23448552
Question 3
[latex]\LARGE5\dfrac{1}{2}\times6\dfrac{3}{8}=[/latex]
https://video.bccampus.ca/id/0_iismlgjd?width=608&height=402&playerId=23448552
Question 4
[latex]\LARGE7\dfrac{5}{9}\times8\dfrac{5}{7}=[/latex]
https://video.bccampus.ca/id/0_x03fh0rj?width=608&height=402&playerId=23448552

