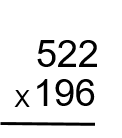9 Multiplying Whole Numbers
Multiplying Small Whole Numbers
As Harpreet’s company grows, he need to buy work vans for himself and his employees. He’s able to get a deal and buys 4 vans. Each of those vans needs to be equipped with tools, so he starts with wrenches. He decides that each van needs 5 wrenches. How many wrenches would that be in total?
This is an example of multiplying whole numbers. The way we could sound it out or write it is as follows:
[latex]\LARGE\text{Four times five OR }4\times5[/latex]
If we looked at it from a more visual perspective, it would look like this:
In this case we could physically count up all the wrenches, and we would end up with 20. We could also count up each row of 5 and add them as follows:
[latex]\LARGE5+5+5+5=20[/latex]
Or we could take one row of 5 and multiply it 4 times because there are 4 rows. The equation would look like this:
[latex]\LARGE4\times5=20[/latex]
Each method should get us the same answer, but going 4 times 5 gets us to the answer quicker. If we were to multiply larger numbers such as 8 time 9 (8 × 9), we could spend a long time counting wrenches or a long time adding numbers. Multiplication simplifies the process.
Before moving on to multiplying larger numbers, why don’t we go through another example of multiplying smaller numbers and use visuals to help us with our answer.
Example
Harpreet decides to buy some screwdrivers for the van and decides that each van needs 7 screwdrivers. He also decides to buy 2 extra sets for the shop. In total he decides to buy 6 sets of screwdrivers.
The first thing we should do is write the question in a form that we can work with.
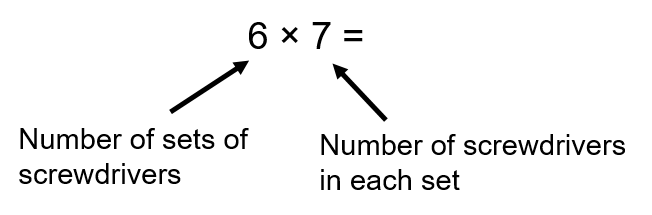
Remember you can also think of it like this:
[latex]\LARGE7+7+7+7+7+7=[/latex]
And once again we could look at it visually and count up the screwdrivers.
If we were to count them up, we would find that we have 42 screwdrivers. If we took our calculator and plugged in 6 times 7, we would get the same answer. If we added 7 plus 7 plus 7 and so on, we would also end up with 42.
Now, we don’t want to have to go through all that work of counting screwdrivers every time we multiply small numbers together. What students end up doing is using their calculator or just memorizing their “times tables.” Times tables are a list of numbers being multiplied, starting at 1 times 1 and going up to 12 times 12. Take a look at the picture to the left to get and idea of what I’m talking about here. The idea is that you memorize these time tables so that when you see small numbers being multiplied, you can just access your memory for the answer.
Although memorizing your times tables is great for small numbers, you still will run up against multiplying larger numbers. The following explanation goes through how we tackle this issue from a mathematical viewpoint.
Multiplying Large Whole Numbers
Suppose that we want to multiply large numbers together. How do you think that would be done? The following method is used to calculate large whole numbers, and we’re going to go right to an example complete with the steps for this one as its quite the process, and we really don’t want to go through this twice.
What is the product of four hundred and thirty seven times three hundred and ninety two?
The word “product” in math terms means the multiplying of two numbers together.
One thing to keep in mind is that the process we are going to work our way through here takes some time and is a lot of work. If during the process you are asking yourself, Would it be easier to just use a calculator?, you would have a good case. But the point of this exercise is once again to help with our understanding of how numbers go together. Remember that once you understand the basics of math, the more difficult concepts will be handled more easily. Taking the time now to fully understand the concept will help you down the road and save you money down that same road.
Example
[latex]\LARGE437\times392=?[/latex]
Step 1: As always, the first step is to put the question in a format that is easy to work with.
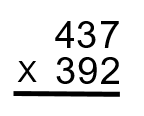
The procedure is generally just multiplying a bunch of smaller numbers together to finally get the larger number. This is where knowing your times tables really comes in handy. The number on the bottom of the equation (in this case 392) is going to be worked with and changed much more than the upper number (437).
Step 2: We start the process by acting as if we are just multiplying the 437 by 2, the number in the ones column. So think of it as looking like the equation below.
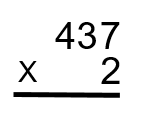
How this works is that you will first take the 2 and multiply it by the 7, then the 2 will be multiplied by the 3, and finally the 2 will be multiplied by the 4. Now this doesn’t all occur in one step. Take a look below to see how this is done.
To start with, multiply the 2 by the 7 to get 14 (2 × 7 = 14).
Enter the 4 into the “ones” column and carry the 1. Remember carrying the one? As the number 14 is too large to be put into the ones column, we have to take the extra and carry it into the next calculation with the tens column.
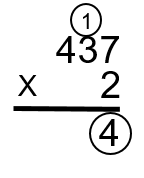
Step 3: Now multiply the 2 by the 3 to get 6. The 1 that we just carried is then added to the 6 to get 7. Put this answer in the tens column (2 × 3 + 1 = 7).
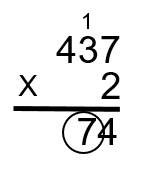
Step 4: Take the 2 and multiply it by the 4 to get 8. Put this number in the hundreds column (2 × 4 = 8).
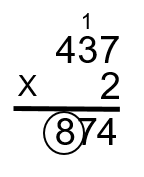
Note: 874 is not the final answer. We still have a few steps to go. Once again you might be asking yourself if doing this with a calculator would be easier, and you’d be correct. It would be way easier but working through the question using this method will help you visualize the process behind multiplication.
Also, before you move on, take a second and go back through the initial steps. Make sure you understand the process we just went through.
Step 5: The next step would be to do the same thing with the number in the tens column. In this case, the 9. Think of it as looking at the equation like the one below.
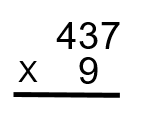
Note the empty space beside the 9. When we begin to take the 9 and multiply it by the number 437, this empty space in the ones column beside the 9 must be taken into account. This is done by placing a zero to start the process and placing it in the ones column. It would look something like is shown below.
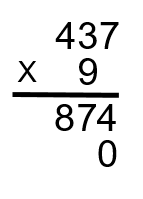
Step 6: Now go ahead and multiply the 9 by all three numbers in the top portion of the equation, starting with the 7. When we take the 9 and multiply it by the 7, we get 63. The 3 is placed in the tens column below the 7 and then carry the 6 (9 × 7 = 63).
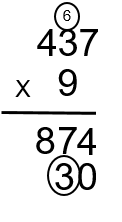
Step 7: Next multiply the 9 by the 3 to get 27. We then add the 6 that was carried over to get 33. The 3 goes in the hundreds column below the 8 and the other 3 is carried into the hundreds column to be used in the next calculation(9 × 3 + 6 = 33).
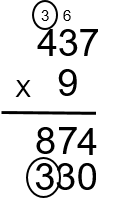
Step 8: The 9 is then multiplied by the 4 to get 36. Then add the 3 that was carried over to get 39. As this is the last calculation for this part, put the 3 and the 9 into the answer. (9 × 4 + 3 = 39)
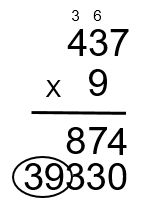
Now do the same procedure using the 3 from the number 392. As the 3 is from the hundreds column, it can be thought of as looking at the equation below. Once again, in the answer we have to account for the fact that we are using a number in the hundreds column and add two zeros in the answer to start off the process.
Step 9: Take the 3 and multiply it by the 7 to get 21. Repeat the same procedure as before (3 × 7 = 21).
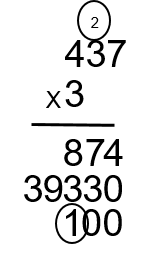Step 10: Now take the 3 and multiply it by the 3 to get 9 and add the 2 carried over from the first multiplication. This will give you 11 (3 × 3 + 2 = 11).
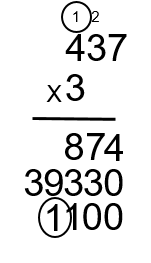Step 11: Take the 3 and multiply it by the 4 to get 12. Add the 1 to get 13 (3 × 4 + 1 = 12).
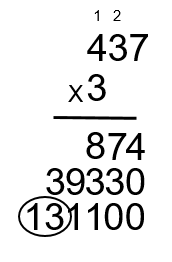
Step 12: Finally, add up the 874, the 39,330 and the 131,100 together to get your final answer.
You might want to do a few things at this point. One is take a break and relax. That was a lot of work to go through. Take a minute to visually work through the process in your mind. If you feel you need to, go back through the work again and make sure you understand what is going on.
The second thing you might want to do at this point is check the answer using a calculator. Plug the numbers in and see what you get.
[latex]\LARGE437\times392 =171,304[/latex]
Practice Questions
Try a couple example questions yourself, and check the video answers to see how you did. Remember that this is a long process so take your time and pay attention to detail.
Question 1
Question 2
