18 Ratios and Fractions and How They Relate to Percentage

What does a ratio have to do with percentage? What does a fraction have to do with percentage? What is a ratio? These are all good questions, and we’ll answer them here. Percentages, ratios, and fractions are all very similar and can be used to represent numbers in different ways, but with similar outcomes.
We already went through fractions in a past chapter, so we know what those are all about. We should take a bit of time to talk about ratios and what they are.
Mathematically speaking, a ratio is a relationship between two numbers. If we were to once again order a pizza and eat 3 of the 8 slices, we could look at that as a ratio. We ate three-eighths of the pizza. Written as a ratio, this looks like:
[latex]\LARGE3:8[/latex]
Notice how the ratio is written. It has its own style, just like a fraction does. A ratio of 3:8 means that we have eaten 3 of the 8 pieces in the pizza. We could also write a ratio that identified how many pieces of the pizza were eaten and how many were not eaten. The ratio for that would look like:
[latex]\LARGE3:5[/latex]
In this case, 3 pieces of the pizza were eaten while 5 pieces were not. Regardless of which way we describe our pizza eating, what we are dealing with is the relationship between two numbers.
Here is another example: let’s say we are on a job site, and we have to install some pipe. We have 42 feet of plastic pipe and 79 feet of steel pipe to install. What is the ratio of plastic pipe to steel pipe that we need to install?
The answer:
[latex]\LARGE42:79[/latex]
Another question might be how much of the pipe is plastic in relation to how much total pipe we have. In this case, the ratio would look like:
[latex]\LARGE42:121[/latex]
In this case, the 121 is derived from adding the plastic pipe and the steel pipe lengths together.
[latex]\LARGE42+79=121[/latex]
At this point, you might be thinking that this looks and sounds familiar, and you would be correct. Ratios are similar to fractions, and each ratio can be written as a fraction.
[latex]\LARGE\dfrac{42}{121}[/latex]
We would say that 42 feet out of a total of 121 feet of pipe is plastic.
All right: we’ve added a few new things to our math library here, but you might be asking right about now, “Aren’t we dealing with percentages in this chapter? How does all this ratio and fraction stuff relate to percentages?”
The idea is we can take these ratios or fractions and turn them into percentages by making the ratio or fraction out of 100. In truth, we don’t even need to make a ratio or fraction out of 100 to do this, but it’s a good place to start our understanding of the math behind the whole process.

We are at a point where we can finally introduce you to some new people in the story. For the story of percentage, we’re going to use apprentices from carpentry, electrical, and plumbing, in addition to statistics.
Note: all the statistics are just made up.

A trades college teaches many trades, including carpentry, electrical, and plumbing. There are currently 97 carpentry apprentices, 123 electrical apprentices, and 80 plumbing apprentices at the college.
The college likes to keep statistics on apprentices, including what percentage of all the apprentices each of the three trades holds. The question is, how do we go about this?
The first thing we should do is add up the total number of apprentices in each of the three trades.
[latex]\LARGE97+123+80=300[/latex]
What we can do now is put each of the apprentice totals into both a ratio and a fraction of the whole.



If percentages are based on 100, then we have to translate the ratio and the fraction into forms based on 100. In other words, we have to make it so that the number on the right in the ratio is 100 and the denominator in the fraction is 100. For this, we have to go back to our work with fractions.
We’ll start with the 97 carpentry apprentices. We have 97 apprentices out of a total of 300. Our goal here is to get this fraction down to a point where the denominator is 100.
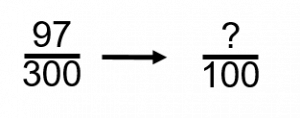
We are essentially reducing the fraction. Luckily for us, going from 300 down to 100 is quite easy. We just divide the denominator by 3, and then also divide the numerator by 3.
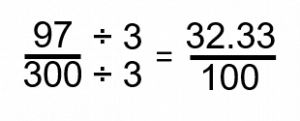
We could now write this number as a ratio.
[latex]\LARGE32.33:100[/latex]
What we end up with is the fact that 32.33% of the trades apprentices are carpentry apprentices. Once we find out the number of carpentry students per 100 students, we automatically have our percentage. In just a bit, we’ll talk about working with numbers that don’t give us a nice even number of 100 and simply translate to percentage in one step. But for now, let’s continue on with our apprentices.
Example
Find the percentage of electrical students.
Step 1: Put the numbers into an equation that we can work with. In this case, put the numbers into a fraction.
[latex]\LARGE\dfrac{123}{300}[/latex]
Step 2: Turn the fraction into one with a denominator of 100.
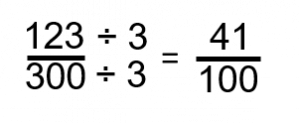
As a ratio, we would have:
[latex]\LARGE41:100[/latex]
And finally, as a percentage, we would get:
[latex]\LARGE41%[/latex]
Practice Question
Now calculate the percentage of plumbing apprentices. Check the video to see if your answer is correct.
https://video.bccampus.ca/id/0_dloiiah6?width=608&height=402&playerId=23448552


The next step actually makes the whole process of finding percentages easier. Remember that “percent” really means out of 100, and in the last section, we took our numbers and made them into fractions with denominators of 100. In this section, we skip that whole procedure and just take the numbers we have and work with them as they are.
We’ll go back to our apprentices for this. Out of the total of 97 carpentry apprentices, there are 57 with a grade of “A” or “B.” What percentage of them have an “A” or “B”? We could go back to our old ways and get to a fraction with a denominator of 100, or we could simply divide the 57 by the 97.
Mathematically, it looks like this:
[latex]\LARGE57÷97=0.59[/latex]
Now take the 0.59 and turn that into a percentage by multiplying the 0.59 by 100. This moves the decimal point 2 spots to the right and leaves us with a whole number. It’s as simple as that.
[latex]\LARGE0.59\times100=59%[/latex]
Example
Using the same method we just used with the carpentry apprentices, find the percentage of plumbing students in the trades college.
Step 1: Write down the equation in a format we can use.
[latex]\LARGE80÷300=?[/latex]
Step 2: Work this out in your head. Just kidding: grab your calculator and plug the numbers in.
[latex]\LARGE80÷300=0.267[/latex]
Step 3: Multiply the answer by 100 to put it into a percentage.
[latex]\LARGE0.267\times100 = 26.7%[/latex]
Practice Questions
Try these practice questions. You can either change each number into a fraction with a denominator of 100, or you can divide one number by the other. The choice is yours, but the video answers will go through both ways.
Question 1
The electrical students are wiring an electrical project as part of their practical mark. The students must receive a minimum of 35 out of a possible 50 marks. What percentage is that?
https://video.bccampus.ca/id/0_hardemes?width=608&height=402&playerId=23448552
Question 2
The plumbing students have been asked to move a bunch of pipe from one side of the shop to the other. There are 279 pieces of cast iron pipe that have to be moved. At the end of the day, they have moved 222 pieces. What percentage of the pipe have they moved?
https://video.bccampus.ca/id/0_ihhz5g2j?width=608&height=402&playerId=23448552
Question 3
Referring to question 2, what percentage of the pipe do the students still have to move in relation to the original amount?
https://video.bccampus.ca/id/0_1nyxdvv8?width=608&height=402&playerId=23448552

