12 Understanding Decimal Notation

We started by going through whole numbers, then we moved onto fractions, and now we will look at decimals.

We start this story with Chad. Now, Chad is not an apprentice, like the people in the first two stories, but rather someone who received his Red Seal Electrical Ticket a number of years ago. He then went on to start his own electrical company, which he still runs today.

After owning his own business for several years, Chad recognized the fact that apprentices coming through the system could use some advice about starting and running a company, especially when it came to the money portion. As Chad has some experience in this, he decided to start a course for apprentices wishing to start their own businesses.

When dealing with numbers, we don’t always have the luxury of working with just whole numbers. If we referred back to the last chapter and looked at fractions, we would see that a fraction represents a part of a whole number. Decimals are the same in that they represent a part of a whole number. The difference is that decimals are written with a different notation than fractions. Decimal notation allows us to visually quantify how much of a whole number we are dealing with.

In his first class, Chad starts off by talking about the price of tools and materials. He starts with a hammer priced at $12.47. Note that the cost of the hammer is not exactly $12, but a little more than $12. This is where decimals come into play. The numbers after the point (.) , also known as the decimal point, are called decimals.

Each dollar contains 100 cents. In fact, the word “cent” means 100. Think of a century: it has 100 years in it. All decimals are based on the number 10 and can be referred to as base 10. These numbers include 10, 100, 1000, 10000, and so on. If we were to relate this to fractions, we would be dealing with fractions that have a denominator of 10, 100, 1000, 10000, and so on.

Although we only have two decimal places to worry about when dealing with money, we can continue a decimal on for as long as we want. For instance, the number pi (3.14 or π) actually continues on forever and has no ending. Check it out:

This just shows pi to the first few dozen decimal places, but there are lots more.

What we need to do is get an understanding of the decimal system and how it works. Take a look at the following number.

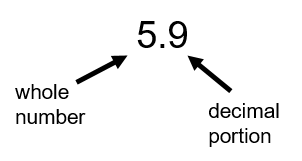
Back in Chapter 1, we dealt with the place value system for whole numbers (see The Place Value System). Decimals follow a similar pattern that starts with the first number to the right of the decimal. In our example of 5.9, the pattern would begin with the 9.

Back to Chad. In Chad’s lecture, he stresses the importance of detailed accounting when dealing with your own business. Now, we all know that there are 100 cents in a dollar, and making sure that you get the cents correct when accounting is important. Rounding up or down to the nearest dollar and being “close enough” won’t cut it. Exact dollar and cent amounts are important, so Chad deals with numbers that go to the second decimal place. Take a look at the number below (which we could assume represents dollars and cents) to see what places the digits are in before and after the decimal place. Let’s use the hammer example of $12.47.

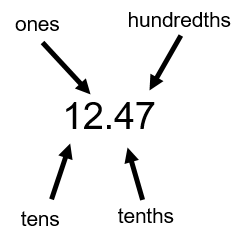
Think of the 0.47 as it relates to money. It would represent 47 cents out of a possible 100 cents. What does the 4 represent by itself? Well, in terms of a dollar, it refers to 40 cents, or 40 out of 100. This is all good, except for the fact that the 4 is actually in what is referred to as the tenths place. What the number is indicating is that we have 4 out of a possible 10 parts. The tenths place can be looked at as being split up into 10 parts, and we have 4 full parts.

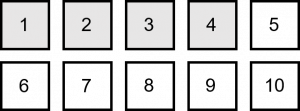
The next step here is to visualize what the 7 is all about. The 7 is in the hundredths place, which means that we have 7 out of a possible 100.

The idea here is to take each box and break it into even smaller parts. The first four boxes are already shaded grey because they represent 4 complete boxes or 40 cents. What we do next is take the fifth box and break it into 10 parts.

Question: If we were to break all 10 boxes into 10 small parts, how many would we have?

[latex]\LARGE10\times10=100[/latex]

We would end up with 100 parts, or we could look at it like 100 cents. Now, take the fifth box out, divide that box into 10 parts, and fill up 7 of them.

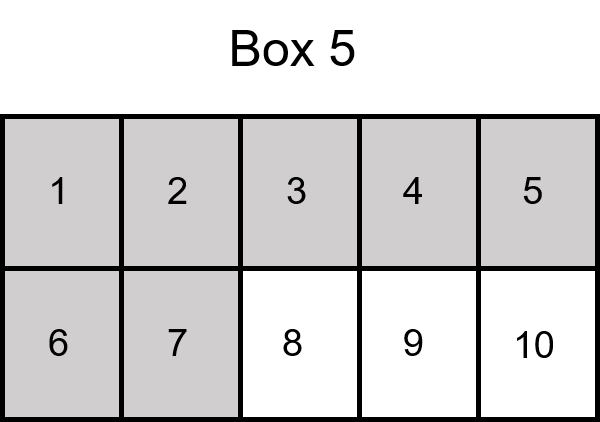
Imagine that each of the original 10 boxes are split into 10 even parts. What gets crazier is that we could then take each of those 100 boxes and split them into another 10 parts each. What this would leave us with is a number that takes us to the thousandths place, because we would be splitting things up into 1000 parts. What we are really doing with decimals is taking a whole number and breaking it down into parts, similar to fractions. In fact, if we were to look at decimals like fractions, this is how we would think about it:

[latex]\LARGE\dfrac{1}{10}=0.1[/latex]

[latex]\LARGE\dfrac{1}{100}=0.01[/latex]

[latex]\LARGE\dfrac{1}{1000}=0.001[/latex]

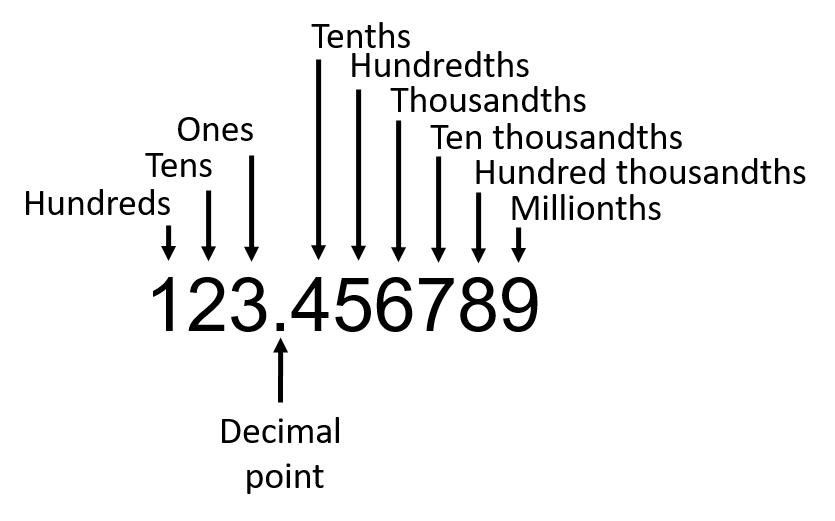
Now that we have the first three digits after the decimal point figured out, let’s work our way even further. Take a look at the number below. To the left of the decimal point is the whole number, and to the right is the decimal or part of a whole number.

[latex]\LARGE123.456789[/latex]

Note: 1, 2, and 3 are all part of the whole number, and 4, 5, 6, 7, 8, and 9 are all part of the decimal. Using the place value system for both whole numbers and decimals, we would end up with the following:

• 1 = hundreds place
• 2 = tens place
• 3 = ones place
• (.) = decimal
• 4 = tenths place
• 5 = hundredths place
• 6 = thousandths place
• 7 = ten thousandths place
• 8 = hundred thousandths place
• 9 = millionths place

Let’s go through a couple quick examples, just to make sure we are all on the same page.

Try another example.