General Physics Remote Lab Manual
General Physics Remote Lab Manual by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.
General Physics Remote Lab Manual by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.
1
This remote learning lab manual was created to guide students in 200-level introductory/general physics courses toward meeting the first outcome in the science category of the Associate of Arts Oregon Transfer Degree:
Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The labs were initially created in response to the remote learning conditions created by the Covid-19 Pandemic and were piloted during the 2020-2021 academic year. Based on instructor observations and student feedback, and with support from OpenOregon, the labs were improved, edited, and compiled into a General Physics Remote Learning Lab Manual.
The lab design goal was to adapt existing F2F labs (already aligned to AAOT science outcome #1) for a remote learning environment without abandoning the pedagogical advantages provided by combining guided inquiry methods with specialized physics education equipment, such as digital sensors and unique demonstration apparatus. Therefore, many of the labs contain embedded videos of experiments being performed and links to open-access Google spreadsheets containing the data produced by equipment during the experiments. In many cases overlay effects have been added to videos to provide additional experimental parameters, direct students’ attention to important occurrences, or and assist with understanding of the experimental methods. The data in the spreadsheets has been edited to remove irrelevant data (e.g. acceleration data automatically collected by lab software before the release of a moving fan cart).
As with the original F2F labs, the remote labs follow a guided inquiry format. The students are provided with the objectives of the lab and step-by-step guidance through the process necessary to meet the objectives. Students are asked to enter results, record progress, and answer critical thinking questions about their work. Adaptation to remote but quasi-synchronous learning included increasing the embedded guidance in the labs to a relatively heavy level. For example, the original F2F labs asked students to fit data with the type of function that corresponded to the model they were testing. This required students to stop and think critically about how their process related to the overall concepts we were studying. Groups often asked the instructor for help with this step, which generated a learning interaction with the instructor and provided both student and instructor with early-and-often feedback. In the remote labs the students are now asked a series of guiding questions that direct them toward the correct choice of fit function. While these adaptations have allowed student to make significant progress between interactions with the instructor I have found that students do still require roughly 1-3 instructor interactions per lab to complete them successfully. As such, the labs current state these labs might not be amenable to a totally asynchronous learning environment.
Physical science labs often focus on the experimental reverification of well-established physicals laws and theories, in which case specific results are expected and error analysis is focused on the difference between expected and observed results. The reverification type of lab can lead to frustration and even increase confusion about the physics concept being tested when the results differ significantly from what is expected. Furthermore, students may end up repeating experiments until an expected result is achieved, with little thought on why the results were different for each trial, in direct opposition to the real scientific process. A goal of this lab manual was to increase focus on scientific models. Students gain experience with well established physics concepts by applying them to create models used to make predictions. The need for assumptions in creating a model is explicitly addressed and students are asked to think critically about the affect of various assumptions on the validity of models in different situations. As in research science, experimental data are analyzed in order to produce results for comparison to prediction. Students are asked to think critically about differences between predictions and results in the context of model assumptions and measurement uncertainty (rather than aiming for a small difference).
All of the labs follow the same basic structure, as outlined below:
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
In some cases, guidance in developing a model for predicting the results of experiments for comparison to results. In all cases, guidance in analyzing by calculating statistics, creating graphs, fitting functions, and estimating uncertainties
Students are asked to consider the results of their analysis and modeling and form conclusions with explanations of the reasoning behind their answers. The reasoning should rely on the results of analysis and modeling work as well as additional knowledge from outside resources, such as the textbook.
Students are guided through the process of extending their thinking to make connections between their results and other physics concepts. For example, by reducing assumptions to build a more comprehensive model, considering additional sources of error, or examining their results in the context of more general physics theories.
2
This remote learning lab manual was created to guide you toward meeting a learning outcome similar to that of the Associate of Arts Oregon Transfer Degree:
Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
In order to meet the desired outcome, the labs use a guided inquiry format. You will be provided with the objectives of the lab and step-by-step guidance through the process necessary to meet the objectives. To help guide your thinking and provide your instructor with information to assess your results, the lab will ask you to enter results, record progress, and answer critical thinking questions about your work. The labs are designed to challenge you. Will likely need to ask for help from your instructor at several points during each lab, and that is expected and normal. To maximize your own learning, follow these tips.
All of the labs follow the basic structure outlined in the example below, which also provides tips about what you are expected to provide for answers within section.
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
In some cases, guidance in developing a model for predicting the results of experiments for comparison to results. In all cases, guidance in analyzing by calculating statistics, creating graphs, fitting functions, and estimating uncertainties
You will be asked to consider the results of their analysis and modeling and form conclusions with explanations.
You are guided through the process of extending their thinking to make connections between their results and other physics concepts. For example, by reducing assumptions to build a more comprehensive model, considering additional sources of error, or examining their results in the context of more general physics theories.
3
The following people were instrumental in the creation of the General Physics Remote Lab Manual. Sole responsibility for errors, including but not limited to, grammatical, typographical, technical, attribution, format, and export errors, lies with the author.
Financial support for the creation of Body Physics was provided by OpenOregon
Amy Hofer, Coordinator, Statewide Open Education Library Services
Jennifer Lantrip, MSLIS, Reference Librarian, Umpqua Community College
Dr. Lawrence (Mick) Davis is an Associate Professor of Science at Umpqua Community College (UCC) in Roseburg, OR where he teaches General Physical Science, General Physics, General Physics with Calculus, and Water Resource Science. In his spare time Mick enjoys alpine climbing, volunteering with Eugene Mountain Rescue, working with UCC’s wrestling teams (men and women), participating in outreach activities such as STEAMHub, writing/maintaining an OER textbook on the physics of the human body and pedagogical research involving learning analytics. Mick’s interests in STEM education (and in body physics) were both sparked by his time at Pacific University where he earned a B.S. in Physics and a top-10 national ranking in wrestling. Mick’s body physics interest continued through graduate school at the University of Oregon (UO) where he earned a Ph.D. in physics and traded wrestling for climbing as an excuse to get out of the lab. Mick’s research focused on the growth, morphology, and optical properties of metallic nanostructures, but he also worked on a collaborative project with the Oregon Institute of Neuroscience and started a consulting company to fulfill a local industry need for physical modeling of stream temperature. The UO is also where Mick met his wife Liz, who is an R.N. and clinical instructor for the Nursing Program at UCC. Raising their two young children has reduced time spent climbing, but provided a whole new source of interest in both neuroscience and the physics of the human body.
1
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
1) Calculate the distance an object would fall in 0.02 seconds, assuming it was dropped from rest and ignoring air resistance. Show your work below.
2) Convert your answer to cm, show your work below.
3) Create a column in a spreadsheet with time values separated by 0.02 s. Use the formula feature of the spreadsheet software to repeat the calculation of fall distance for each of the time values in the table and convert units to cm. You should get a table like this, but with many more rows, and the question marks replaced with values calculated by your formula:
| Time (s) | Drop Distance (cm) |
| 0.02 | ?? |
| 0.04 | ?? |
| 0.06 | ?? |
Use the first 0.02 s calculation that you did by hand to verify that the formula is working correctly. Fill the table until the drop distance you calculate are larger than the total length of your ruler. Check with your instructor if you are unsure about your spreadsheet results.
4) Are the distances in your spreadsheet evenly spaced? Explain why or why not. [Hint: Look back at the equation you used to calculate the distances.]
5) Have a friend or family member hold the ruler the top while you place your thumb and index finger about 3 cm apart on either side of the very bottom edge of the ruler, as if you were about to pinch the card between your fingers. Without giving any signal, the card holder will let go and you will close your fingers to catch the ruler. Whatever distance your fingers end up on when you catch the ruler, that is the distance the ruler fell while you reacted. This video shows what the experiment will look like, though our units and analysis methods will be different. You can then read the fall time for that distance from your spreadsheet. That was your reaction time. Record your first fall distance and corresponding reaction time value below. Also indicate any difficulties that you had in performing this experiment.
6) Repeat this experiment 10 times, recording your measured reaction time for each trial in a spreadsheet, which should look like this.
| Trial | Reaction Time (s) | Time Uncertainty (s) |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
7) Graph the reaction time vs. trial number in a scatterplot. Give the graph a name and label the axes, including units.
8) Your fingers are wide, squishy, and do not have sharp edges so the uncertainty in measuring the location of your fingers is not determined simply by precision of your ruler. Estimate the actual uncertainty in reading off the location of your fingers and explain your reasoning.
9) The uncertainty in the location of your fingers leads to an uncertainty in the reaction time measurement. Even though you are assuming same uncertainty in each distance measurement, that does not mean the time uncertainty is the same for each trial (because fall time and distance are not linearly related). However, we can use your spreadsheet of fall times and distances to estimate the time uncertainty for each trial. For each drop distance you measured, look the distances above and below that fall within the finger location uncertainty you explained above. Then look at the range of fall times that correspond to that range of distances. That is the uncertainty in the fall time that corresponds to the location uncertainty. Do this for each trial and record the time uncertainty in another column to the right of your experimental reaction time data.
10) Add vertical error bars to you graph to represent the uncertainty in reaction time for each trial. You can use the custom error bar option to select the uncertainty column and automatically assign the correct error to each data point on the graph. The videos in the lab manual introduction demonstrate how to do this. There was no uncertainty in the trial number because there was no measurement made, you simply counted the trials, so we will not add horizontal error bars (use the fixed size option and set the size to zero).
11) Calculate the average, standard deviation, and standard error of the mean (SEM) of your 10 reaction time values. You may use the built-in functions of the spreadsheet to perform these calculations. The videos in the lab manual introduction demonstrate these calculations.
The standard deviation tells us about variation in the data (how close together the value are). We often use the standard deviation calculated from a set of measurements an estimate of the uncertainty in making that particular type of measurement, assuming we were measuring the same quantity each time. However, it is likely that your reaction time was actually different each time, so we can’t really assume the standard deviation represents the uncertainty for a single reaction time measurement. Instead, the standard deviation represents the lack of consistency in your reaction time from one trial to the next.
12) Due to the lack of consistency, we would not be very certain that a small number of reaction time measurements would be representative of your average reaction time. However, the uncertainty in the average value can be reduced by averaging many values. That uncertainty is often estimated by the SEM (based on the assumption that the variation in the values is random). Using the SEM as an estimate of the uncertainty in your average reaction time, report your average reaction time with uncertainty in the standard format: average + uncertainty in the average.
13) Calculate a percent uncertainty in the average. Report your average reaction time with % uncertainty in the standard format: average + percent uncertainty in the average (%).
14) Apply a trendline to the plot of the data and display the trendline equation and R2 value on the graph, and record each here:
15) If a significant amount of the variation in the data is actually caused by a real trend in the data (such as getting faster or slower with more trials) then you did not actually attempt to measure the same thing 10 times (reaction time), you measured 10 different things one time each (reaction time after a certain amount of practice). In that case the variation is caused by the trend, not by measurement error or random inconsistency in your reaction time and the SEM is not necessarily representative of the uncertainty in the average value. Do the data suggest that there is a trend (correlation) in the reaction time vs. trial data? Explain in terms of the error bars, the trendline equation, and the R2 value.
16) Are you confident that the average reaction time value you measured is representative of your actual typical reaction time? Explain your reasoning, which should incorporate your answer above and the SEM value.
17) Find a peer-reviewed research article on human reaction time and compare the result of that study to your result and the online reaction tester result. Does your result seem reasonable in comparison? Do the values agree within the combined uncertainty in your measurement and theirs?
18) Use this online reaction time tester to quickly make another 10 reaction time measurements. Find the average, standard deviation, and SEM of those 10 results and record below.
19) Contrast the results with those of your fall-time experiment. Were the average reaction times measured by each method in agreement? (Do the average + SEM of each result overlap?) Explain.
20) Do you feel that the fall-time method is a reasonable way to test reaction time? Explain.
2
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
Wheeled carts running level tracks are sometimes used to learn about various types of motion, including accelerated motion. For that purpose, fans can be attached to the carts to cause them to accelerate. The video below demonstrates shows such a setup used for different accelerated motion experiments.
The data collected during the demonstrations seen in the video are available in an online spreadsheet. You can copy and paste the data into your own spreadsheet for plotting and analysis. Be sure to review the videos on plotting, adding trendlines, and interpreting R2 values found in the introduction if you need a refresher on those skills.
1) If the acceleration is constant, what kinematic equation should describe the position of an object as a function of time? Write it below and state the type of function (e.g. constant, linear, quadratic).
2) Plot the position vs. time data for the cart that changed direction. Be sure to provide a title and axes labels with units.
3) Based on your previous answer about the function type, apply the appropriate type of fit equation to the data and record the resulting equation and the R2 here:
4) Comparing your fit equation to the kinematic equation it represents, you will see that the fit equation provides you values for the acceleration and initial position and velocity. Write the values for initial position, velocity, and acceleration below. You have applied a kinematic model to the cart motion and extracted the values for those three parameters of the model. The acceleration was an unknown parameter because you did not have data on that value. (Keep in mind that your spreadsheet program doesn’t know you are doing kinematics so it might default to calling the vertical variable “y” and the horizontal variable “x” even though we plotted position, which we often call “x” on the vertical axis and time, which we usually call “t” on the horizontal axis. Replacing the fit “x” with “t” and the “y” with “x” will help you make the comparison).
5) Calculate a % difference between the measured initial position (first position value in the data) and the initial position extracted from the model fit. Do the same for the initial velocity values. Show your work.
6) Does the position analysis suggest that the kinematic equations successfully model this data (and therefore the acceleration is constant)? Explain in terms of the R2 value and the accuracy of the initial velocity and initial position parameters.
7) If the acceleration is constant, what kinematic equation should describe the velocity as a function of time? Write it below and state the type of function (e.g. constant, linear, quadratic).
8) Plot the velocity vs. time data for the cart that turned around. Be sure to provide a title and axes labels with units.
9) Based on your recent answer about the function type, apply the appropriate type of fit equation to the data, and record the resulting equation and the R2 here:
10) Comparing your fit equation to the kinematic equation it represents, you will see that the fit equation provides you values for the acceleration and initial velocity. Write the values for initial velocity and acceleration below. You have applied a kinematic model to the cart motion and extracted the values for those three parameters of the model. The acceleration was an unknown parameter because you did not have data on that value.
11) Calculate a % difference between the measured initial velocity (first velocity value in the data) and the initial velocity extracted from the model fit. Show your work.
12) Does the velocity analysis suggest that the kinematic equations successfully model this data (and therefore the acceleration is constant)? Explain in terms of the R2 value and the accuracy of the initial velocity parameters.
13) You now have two acceleration values that were extracted from the kinematic models, one from the position model and one from the velocity model. Calculate a % difference between these two values to determine how well they agree. Also calculate the the average of these two acceleration values.
14) Overall, do the results of your analysis of position and velocity data indicate that the kinematic equations successfully model the motion of the cart and therefore the acceleration is constant? Explain.
15) Would you trust the average value of the acceleration that you found by applying the kinematic models? Explain.
The real advantage of building and testing models is that when a successful model is discovered then we can use it to make predictions of unknown quantities. Let’s use the kinematic equations as a model to predict unknown quantities in a new situation.
16) Plot the position vs. time data for the second trial, when the cart does not turn around. You will notice that the data for the beginning and end of the motion are missing and that no acceleration data is available. Therefore, we don’t yet know the acceleration or the initial and final values of position and velocity.
17) Fit the position vs. time data with the appropriate function and record the fit equation and R2 value here:
18) Determine the initial position, initial velocity, and acceleration of the cart by comparing the coefficients (numbers) in your fit equation to the variables in the corresponding kinematic equation. Record the values below (don’t forget units).
You now know the initial position, initial velocity and acceleration even though you had no data on those values. You have applied a kinematic model to the cart motion and extracted the values for three unknown parameters of the model. We can now use those parameters to make predictions by simply applying the kinematic equation with those values in place (the fit equation).
19) Now that you know the values of the parameters in the kinematic equation, use it to predict what the final position of the cart would be after at 3 s.
20) Use the acceleration parameter and initial velocity parameter that you extracted to predict the final velocity of the cart at 3 s. (Use these in another kinematic equation).
Using the model to predict values outside the range of data you have is known as extrapolation, that is what we have just done. Using the model to predict values within the range of data you have is known as interpolation. We didn’t interpolate because our data points were very close together (we had high resolution) so we had no reason to interpolate in this case.
3
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The range equation (below) allows us to predict the launch distance, or range, from the launch angle and launch speed.
\begin{equation}
R = \frac{v_0^2 sin(2\Theta)}{g}
\end{equation}
The range equation is derived from the kinematic equations assuming a constant downward acceleration equal to g and zero horizontal acceleration. Therefore, the range equation intrinsically neglects the effects of air resistance. We would like to test the range equation to verify the validity of those assumptions. We can test the equation examining how well it can model experimental range vs. angle data.
Range vs. launch angle data was collected according to the video below. The data is available in an online spreadsheet. You can copy and paste the data into your own spreadsheet for plotting and analysis.
1) Copy and paste the range vs. angle data into the first two columns of your spreadsheet, leaving an empty row at the top for the column labels.
2) Label the two columns, including units.
3) Plot the data. Place the dependent variable (we don’t control) on the vertical axis and the independent variable (what we control) on the horizontal axis. Be sure to provide a title and axes labels with units.
4) Below is an image of the plumb-bob and scale use to determine the launch angle. Based on the image, estimate the uncertainty in the angle measurements. Explain your reasoning.

5) Slow motion video was used to determine where the ball landed in order to measure the range. Several individual frames of one of the videos are shown below. The numbers on the meter stick are 1 cm apart. Based on this information, estimate the uncertainty in the distance measurements. Explain your reasoning.

6) Add horizontal and vertical error bars to your graph based on the uncertainty estimates for angle and range. The following video demonstrates how to make the graph and add the error bars.
Now we will attempt to use the range equation to model the data and extract the unknown launch velocity as a free parameter. This is our only free parameter because all of the other parameters (inputs) to the model are known or measured. This video walks you through the steps, which are also written out below (through step 23).
7) Label the third column “angle (rads)” and enter an equation to convert the angle data from degrees to radians.
8) Choose two cells several columns off to the right of your sheet where you can input the launch speed and the gravitational acceleration. Enter the gravitational constant equal to 9.8 m/s/s. This is a known parameter of the model. Set the launch speed to 1 m/s (for now). We don’t actually know the launch speed, so this is a free parameter that we will attempt to extract from the model. Use adjacent cells to label your two parameter cells, including units, but don’t put the units in the same cell as the values.
9) Label the fourth column “range model” and drop down to the second row of the column.
10) In the second row of the fourth column, enter the range equation to calculate the expected range by referencing the first cell containing the angle in radians and your two cells containing the parameter values. If you chose H2 to contain the gravitational acceleration and H3 to contain your launch speed, your equation would look like this in Excel:
=$H3$^2*SIN(2*C2)/$H2$
Notice that we have used dollar signs to make sure that this equation always references our parameter cells, even if we pull the equation to other cells.
11) Pull-down the cell containing the range equation to automatically calculate the expected range for all of your measured launch angles.
12) Add the model predictions to the existing plot as a new data series.
13) Add a legend to your plot.
14) Appropriately name the the two series “data” and “model” so that the names are reflected in the legend.
15) Make the model roughly agree with the data by making 2-3 attempts at manually adjusting the launch speed parameter.
We don’t want to rely on our eyes to determine how well the model fits the data. Instead, let’s do some basic statistics. We will use maximum R2 estimation to find the launch speed because you have worked with R2 values in previous labs. In other words, we will find the launch speed value that maximizes how well the range equation describes the observed variation in the range data. In previous labs we asked Excel to do the minimum R2 estimation for us, using a function that we chose from the available options. However, none of those functions have a $sin(2\Theta)$ in them like the range equation does, so this time we we will do our own maximum R2 estimation.
16) Create a new column to the right of your model predictions and enter a formula that calculates the difference the observed (measured) and expected (predicted) values and squares that difference.
17) Pull down the formula to apply it to all the pairs of observed and expected range values. Now you have a set of always positive values that are larger when the percent difference between prediction and observation is larger. These are known as the squares of the residuals.
18) In another cell beneath your parameter cells (off the the right), apply the SUM formula add up all values calculated in the previous step. This value is known as the residual sum of squares, or SSres.
19) Below the cell you chose above, enter a formula to calculate the average of all the measured range values.
20) At the top of the column to the right of squares of residuals, enter a formula that calculates the square of the difference between the measured value and the average of all measured values.
21) Again use dollar signs to ensure that when you pull this formula down all of the new formulas will continue to reference the same cell containing the average. Pull the formula down.
22) Now in another cell below your residual sum of squares, sum up all the values you just calculated. This is the total sum of squares, or SStot.
23) Finally, in a new cell calculate the R2 as: 1 – SSres/SStot
24) Now we can start changing the value of the launch speed to maximize the R2. Don’t spend more than a minute doin so. What value did you arrive at for the launch speed?
You may have noticed that by continuing to add more digits to the speed you could continue to maximize the R2 indefinitely. We need to factor in uncertainties to decide how precise our estimate of the launch speed parameter should be.
25) There are sophisticated ways to estimate the uncertainty in the free parameter, but for the purpose of this lab we will take a very rudimentary approach. You may improve the R2 by changing the launch speed, but stop once most of the predicted values are within the error bars on the data. Now check to see how much you need to change the speed in each direction to cause those predictions to move outside the error bars. That range of speeds will define our speed uncertainty.
26) Use the center of the range of speeds you found as the speed value. Use the range of speeds to write the speed uncertainty as + half of the size of that range. Adjust the significant figures in your estimated launch speed to align with your uncertainty and record the speed and uncertainty below.
27) Write your final R2 value:
28) Do the results of your experiment support or refute your hypothesis? Explain.
29) Are the kinematic equations, and the range equation that results from them, a reasonable model for everyday projectiles like small plastic balls, despite the the fact that they neglect air resistance? Explain your reasoning based on the results of this experiment.
If this was a new, unverified model then you would have provided some evidence that your model is valid under the conditions in this experiment because it can describe the data well. You also have used your model to extract the launch speed as a free parameter. If you then measured the velocity another way and found agreement with your model prediction, then you would even stronger evidence that your model is valid under the conditions in this experiment.
30) If you were to repeat the experiment, how might you experimentally measure the launch speed of the ball? Explain what equipment you would use and what procedure you would follow to determine the launch speed.
You may have noticed that the data looks kind of like a parabola and maybe you thought about applying a quadratic fit. Doing so, you will see a good fit with very high R2 and we might consider using that fit as an empirical model to make predictions of range from angle. However, the we would have the range equation model suggesting the range should depend on $sin(2\theta)$ and a quadratic model suggesting that range depended on $\Theta^2$! Both our range equation and the quadratic equation had very high R2, so how would we decide which is the better model?
Just because a model gives a high R2, that doesn’t necessarily mean it has a real connection to the mechanisms being studied. Conversely, just because a model gives a low R2, that doesn’t mean the model is fundamentally flawed.
4
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The following video shows a cart accelerated by a falling mass attached to the cart by a string running over a pully. The experiment was repeated for 5 different cart masses, starting with the empty cart and successively adding four additional masses. The velocity of the cart was measured by the cart’s optical sensor. All of the necessary setup data is available in the video and the recorded velocity data is available in an online spreadsheet. You can copy and paste the data into your own sheet for analysis.
1) Assuming the track is level, what is the vertical acceleration of the cart?
2) In that case the net vertical force on the cart must be zero, so the force of gravity on the cart must be balanced by the __________ force on the cart from the track.
3) We also neglect friction and air resistance so the only horizontal force on the cart is the tension in the string. Write Newton’s Law for the cart in the horizontal direction using $F_T$ for tension and $m_c$ for the cart mass.
4) Neglecting air resistance, write Newton’s Second Law for the hanging mass, $m_h$.
5) This experiment is near the surface of Earth, so you may use $F_g = m_hg$ for the magnitude of the force of gravity on the hanging mass. Let’s choose downward as the positive direction for consistency.
6) Your analysis of the cart gave you an equation for the tension. Assuming no friction in the pulley, the magnitude of the string tension must be the same on both ends. Substitute that result for the magnitude of the tension force in your current equation and set the sign as negative because tension points upward, which we chose as negative.
7) The magnitude of the acceleration for the hanging mass and cart are the same because they are connected by the string. Solve for the acceleration of the mass and cart.
8) We could have arrived at this same result by recognizing that the frictionless pully cannot change the tension in the string. Therefore, this situation is no different from pulling horizontally on the mass with the same force as its weight while it is connected directly to the cart with a horizontal string and no pulley. In that case the only external force on the system is the $F = m_hg$ and the system mass is $m_c +m_h$. Write Newton’s second law for this system and solve for acceleration to verify that we get the same result. Show your work.
9) According to our model, the acceleration should be proportional to $\frac{m_h}{m_h +m_c}$, with what proportionality constant?
First we will use the data in the online spreadsheet to find the acceleration for each trial. There are two methods we can use.
10) The first is to fit the plot velocity vs. time data for each trial and fit the data with a line. If the velocity vs. time data is linear then the ____________ of the fit line will tell you the acceleration. If you choose this method be sure to plot and fit only a subset of each dataset beginning after the cart was released and ending before the hanging mass hit the ground.
11) The second is to find the maximum velocity reached for each trial and then use a kinematic equation to find the acceleration for each trial. You will need to know the distance travelled, which is shown at the end of the video. Show the work of symbolically solving the appropriate kinematic equation for the acceleration.
12) Choose one of the methods above and create a spreadsheet containing the trials and accelerations.
13) Make third column in your spreadsheet which calculates $\frac{m_h}{m_h +m_c}$ for each trial. The cart mass for each trial includes the total accessory mass used for that trial. Make sure these columns are well labeled, including units.
14) Plot the measured acceleration vs. $\frac{m_h}{m_h +m_c}$. Make sure the graph is named and the axes are labeled, including units.
15) Fit a trendline to the data. Record the fit equation and the r2 value here.
16) Does the fit line indicate that the relation between acceleration and $\frac{m_h}{m_h +m_c}$ is proportional as predicted by the model? Explain.
17) Calculate a % difference between the experimental slope and the expected slope (proportionality constant). Show your work.
18) Do your experimental data support the acceleration model you created? Explain.
19) What steps would you take to reduce uncertainty in the measurements for this lab? Explain exactly changes you would make or what equipment you would use, how, and why the uncertainty would be reduced (“I would do better” or “use better equipment” are not sufficient.)
20) Notice that this lab assumed that gravitational mass, used to calculate the gravitational force on objects, and inertial mass, used in Newton’s Second Law, were the same thing. The equivalence of gravitational mass and inertial mass leads to models which accurately predict what we observe. Consequences that have resulted from non-equivalence have not been observed. For example, in the previous lab you were able to model the range of a ball by assuming it’s free-fall acceleration was g, regardless of its mass. The equivalence of gravitational and inertial mass explains why all objects in free-fall near Earth will accelerate at the same rate of g regardless of mass. In this very lab you were able to model the acceleration of the system by inputting a value for inertial mass you found by measuring gravitational mass (with the scale). Design your own experiment to test the equivalence of inertial mass and gravitational mass (other than a free-fall experiment). Describe/explain your experiment.
To learn about how Relativity Theory explains the equivalence of gravitational mass and intertial mass, watch this video.
To learn more and see why the equivalence principles do not suggest that Earth could be flat, watch the second video. To learn about the fundamental source of mass in the first place, watch the third and fourth videos.
5
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
We will setup a small cylinder sitting on a rotating disk, with no other known forces beyond static friction acting horizontally on the object. We will then measure the speed at which the object begins to slide for several different values of the rotation radius and try to model the results. We will need to do a supplementary experiment to find the static friction coefficient ($\mu_s$) between the disk and the cylinder.
Fill in the blanks inside the brackets in the following model derivation.
An object moving in a uniform circle of radius $r$ must experience an acceleration of $a = v^2/r$. Applying Newton’s Second Law to an object moving in a uniform circle with mass $m$, we then have:
$F_{net} =[\,\,]v^2/r$
If static friction alone is providing the net force, then the net force is just static frictional.
$F_f =[\,\]v^2/r$
The max static friction force can be calculated from the empirical formula: $F^{max}_f = \mu_s F_N$. Making that substitution allows us to determine the maximum tangential speed the object can have without slipping.
$ \mu_s F_N= [\,\,]v_{max}^2/r$
For the case of a flat disk, the normal force will be equal to the object’s weight. Near the surface of Earth we calculate the weight as $F_g = mg$. Making that substitution we have:
$\mu_s[\,\,\,\ ]= [\,\,]v_{max}^2/r$
Cancel the masses and isolate $v_{max}^2$ to complete the following equation:
$v_{max}^2 =\,\,\,\,\,\,\,\,\,\,$
This max rational speed model depends on the static friction model: $F^{max}_f = \mu_s F_N$. Therefore, data that support the validity of this model for $v_{max}$ also support the static friction model.
In order to use this model we will want to know the static friction coefficient. The following video shows a model for surface the angle at which an object begins to slide. Applying this model to experimental data will allow us to extract the static coefficient as a parameter.
1) Record the max angle before sliding from the video above.
2) Use the max angle before sliding to calculate the static friction coefficient ($\mu_s$).
3) Create a spreadsheet with these columns:
| radius (m) | time 1 (s) | time 2 (s) | Δ time (s) | Δ angle (deg) | Δ angle (rads) | angular speed (rads/s) | v (m/s) | v2 (m2/s2) |
| 0.045 | ||||||||
4) Use the video at the start of the lab to record the times for two positions of the object just before it begins to slide for each radius trial. The times are seen on the stopwatch and the positions are indicated by the blue arrows. At the end of each trial in the video the blue arrows will remain in place so that you can determine the change in angle between the two positions. Notice that the compass repeats every 90° so you will not be able to simply subtract one angle reading from the other, but instead you will need to take care to to determine the change in angular position. Record the times and change in angle in your spreadsheet.
5) Build formulas in your spreadsheet to calculate the remaining values in your chart for each radius.
6) Make a plot of $v_{max}^2$ vs. radius ($r$). Be sure to title your graph and label your axes, including units.
7) Apply a linear fit to your data and record the fit equation and R2 value here:
8) If $v_{max}^2 = [\mu g] r$ and you plotted $v_{max}^2$ on the y-axis and $r$ on the x-axis, then the slope of your fit should be __________.
9) Calculate a % difference between the slope you found from fitting the data and the slope calculated from the values above.
10) Our model for $v_{max}^2$ depends on the empirical quantitative static friction model ($F^{max}_f = \mu_s F_N$). Does the data suggest support these two models? Explain. [Hint: Reference the results of the analysis section.]
A common interpretation of the qualitative static friction model is that “static friction is a responsive force that increases to be equal and opposite to whatever force is exerted, up to a maximum limit: $F^{max}_{f,s} = \mu_s F_N$. Once the applied force exceeds the maximum limit, the object slides”"Friction" by OpenStax University Physics is licensed under CC BY 4.0.
However, our model assumes that static friction is the only horizontal force on the object, so our model does not agree with the interpretation above. (According to the interpretation above, the friction force is “responsive” and can’t have a value unless some other force is applied to the object).
11) Adapt the previous interpretation to provide a more complete statement of the static friction model. (Provide an explanation of the responsive behavior of static friction on an object without the requirement that other forces to act on the object). Cite all sources. If desired, you may use the template below by filling in the in the blanks.
“The static friction force between two surfaces adjusts to whatever value is required to _________ __________ between the two surfaces, up to a maximum limit: $F^{max}_{f,s} = \mu_s F_N$. If the force required to _________ __________ is greater than the limit, then _________ occurs.”
12) Notice that while deriving the model we cancelled the inertial mass from Newton’s Second Law with the gravitational mass used to calculate the object’s weight. Therefore, testing this model also provided another test of the equivalence principle, similar to the test we did in the previous lab. Does this new experiment add evidence in favor or against the equivalence principle?
13) Notice that the disk and the cylinder were speeding up over time, so there was not only a centripetal acceleration pointing toward the center, but there was also a small tangential acceleration. The tangential can be found by calculating the change in speed divided by the change in time. For example, in the first trial the time to reach the slipping speed was roughly 60 seconds. Use that time and the slipping speed you found for that trial to calculate the tangential acceleration. Show your work.
The total acceleration is the vector sum of the centripetal and tangential accelerations. These accelerations are perpendicular so we can find the magnitude of the total acceleration with the Pythagorean Theorem:
$a = \sqrt{(\frac{v_{max}^2}{r})^2 + a_T^2}$.
Applying Newton’s Second Law with this total acceleration we get:
$\mu_s mg = m\sqrt{(\frac{v_{max}^2}{r})^2 + a_T^2}$
Cancelling the masses and solving for $v^2$ we find:
$v_{max}^2 = \sqrt{(\mu_s g)^2 – a_T^2}\cdot r$
Before including the tangential acceleration in our model we had: $v_{max}^2 = \mu_s g \cdot r$
14) In both cases the max speed is proportional to the radius, but the slope is different. Calculating the percent difference between $\sqrt{(\mu_s g)^2 – a_T^2}$ and $\mu_s g$ allows us to estimate the percent error in the model caused by ignoring the the tangential acceleration. Do that with the tangential acceleration value you found for the first trial. Show your work.
6
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The following video shows a cart accelerated by a falling mass attached to the cart by a string running over a pully. The experiment was repeated for 5 different cart masses, starting with the empty cart and successively adding four additional masses. The velocity of the cart was measured by the cart’s optical sensor. All of the necessary setup data is available in the video and the recorded velocity data is available in an online spreadsheet. You can copy and paste the data into your own sheet for analysis.
We will build a model for the maximum speed reached by the cart. The maximum speed is reached as the mass hits the floor, after which point the string becomes slack. The model will assume that the work done by the forces of friction and air resistance is negligible compared to the total mechanical energy of the system. In other words, we will assume the mechanical energy of the mass-cart system does not change during the experiment.
1) Write down an equation representing the conservation of mechanical energy for this system. Use the system at rest as the initial state. Use the moment just as the mass hits the floor, after falling a height of $Delta h$, as the final state. Remember that both the mass and the cart are moving at that point.
2) Symbolically solve your equation for the final speed of the system. Show your work.
3) Create a single graph containing plots of the the velocity vs. time data for all 5 trials. Examine your graphs to make sure you have a complete dataset that includes the maximum speed reached by the cart for each trial.
4) Be sure to name your graph and add axis labels with correct units.
5) Use the MAX function in your spreadsheet program to find the maximum speed for each trial. (The data sheet contains an empty row at the top for you to place this function).
6) In a new area of your spreadsheet create a table that looks like this:
| hanging mass (kg) | ||||||||
| cart mass (kg) | ||||||||
| accessory mass (kg) | ||||||||
| height (m) | ||||||||
| accessory masses | system mass (kg) | predicted max speed (m/s) | measured max speed (m/s) | percent difference in speed | initial energy (J) | final energy (J) | percent difference in energy | tension (N) |
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
7) Fill in the values of the experimental parameters, hanging mass, cart mass, accessory mass, and fall height.
8) Use your spreadsheet to calculate the total system mass based on the cart mass, hanging mass, and number of accessory masses for each trial.
9) Use your spreadsheet to apply your model equation to calculate the predicted max speed for each trial. (Don’t forget that that the hanging mass was falling. How does that affect your value for the change in height of the hanging mass?)
10) Enter the measured max speed values for each trial that you found using the MAX function.
11) Use your spreadsheet to calculate the percent difference in the measured and predicted speeds.
12) Use your spreadsheet to calculate the initial mechanical energy of the system.
13) Use your spreadsheet to calculate the final mechanical energy of the system.
14) Use your spreadsheet to calculate the percent difference in the initial and final mechanical energy of the system.
15) Do the data suggest that the effects of air resistance and friction are significant? Explain.
16) According to your mechanical energy model, all of the potential energy in the hanging mass was transferred to kinetic energy in the moving cart and falling mass. The model neglected friction, air resistance, and the transfer of kinetic energy to the pully. Do you expect your model overestimate or underestimate the amount of kinetic energy in the cart + hanging mass system? Do you expect your model your model overestimate or underestimate the speed of the cart? Explain.
17) According to your predicted and measured values, does your model over/under estimate the energy and speed as you expected? Explain.
18) Our data contains additional information that we have not analyzed. We can and actually try to narrow down which of the elements neglected by our model was most likely to have contributed the most to differences between predicted and measured values. Let’s add a few hypotheses that we can test with our data. Fill in the blanks with the correct relation between values (increase or decrease).
19) To test your hypotheses, create the following graphs shown in the table, fit linear trendlines to each, then fill in the table, except for the last row.
| Hypothesis | Graph | Slope | R2 | Hypothesis supported? (Explain) |
| Air resistance | % difference vs. max speed | |||
| Cart Axle Friction | % difference vs. total cart mass | |||
| Pulley Kinetic Energy | % difference vs. max speed | |||
| Pulley Axle Friction | % difference vs. string tension |
20) We have not yet tested the likelihood that friction in the pulley was a main contributor to the percent difference. Let’s add another hypothesis:
21) To test this hypothesis we need to determine the string tension. The tension in the string does work over some distance to increase the kinetic energy of the cart. We can apply the work-energy theorem to model to the cart to model the tension in the string.
Based on your results, what can you say about how the various elements neglected by your model contribute to the % difference in predicted and measured values? [Hint: You hypothesis is basically saying that if the first half of your hypothesis is correct, then the second half should be observed. That does not imply that if you observe the second half, the first half is necessarily correct: If P then Q does not imply if Q then P. Assuming it does is a logical fallacy know as affirming the consequent (sometimes called converse error, fallacy of the converse, or confusion of necessity and sufficiency).
22) Notice that this model assumed equivalence of inertial and gravitational mass. The cart mass, hanging mass, and accessory mass values were all measured using scales, so those were gravitational masses, but we used them in calculating the total kinetic energy. Additionally, the same hanging mass value was used in calculating gravitational potential energy and in contributing to the total kinetic energy of the system. Therefore, similar to previous two labs, this experiment was also a test of the equivalence principle. Does this new experiment add evidence that supports or refutes the equivalence principle?
7
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
For the simplified case of a car hitting a solid barrier that doesn’t move, let’s compare the force peak applied to occupants for the theoretical case of a perfectly elastic car and a perfectly designed crumple zone. We will simplify our problem by analyzing the case of a car hitting a solid immovable barrier. We start by analyzing the first half of the collision (as the car/person comes to rest before bouncing back) and including the car and barrier in our system. We will assume the crumple zone provides a constant resistive force as it crumples and dissipates kinetic energy into thermal energy.
First we start with the Law of Conservation of Energy:
$0 = \Delta PE +\Delta KE$ +\Delta TE
Internal work is done on the car-barrier system to convert KE to TE and we are assuming that work was done by a constant force over the total crumple distance, $x$. In that case $\Delta TE = Fx$. No energy is stored as PE:
$0 = 0 +\Delta KE + Fx$
Expanding the change in kinetic energy and setting the final kinetic energy to zero:
$0 = 0-\frac{1}{2} mv_i^2 +Fx$
1) For this ideal case of the constant force, the average and peak force exerted are the same. Symbolically solve for that force. Show your work.
Again we start with the Law of Conservation of Energy:
$0 = +\Delta KE$ +\Delta TE
In the elastic collision internal work is done on the car-barrier system to convert KE to elastic PE. No energy is stored as TE. Expanding the change in kinetic energy and setting the final kinetic energy to zero:
$0 = \Delta PE + 0-\frac{1}{2} mv_i^2$
We will model the elastic material as a spring, so change in elastic PE is $\Delta PE =(1/2)kx^2$.
$0 = \frac{1/2}kx^2 -\frac{1}{2} mv_i^2$
Expanding the $x^2$ allows us to introduce the Force into the equation.
$0 = \frac{1/2}kxx +\frac{1}{2} mv_i^2$
We recognize that for a spring $F = kx$ and that $x$ and make that substitution:
$0 = \frac{1/2}Fx +\frac{1}{2} mv_i^2$
2) The force is applied at maximum compression distance $x$ is the peak force. Symbolically solve for the peak force. Show your work.
3) Compare the peak force of the elastic collision and the peak force of the dissipative collision. Which is larger, and by how much?
4) The spring force increases linearly with compression distance, so the average force exerted by a spring will be half of the maximum force exerted at maximum compression. Therefore the average force in the elastic collision is half of what you found for the peak force. How does the average force compare between the elastic and dissipative collisions?
5) Does what you found above agree with the Work-Energy Theorem? Explain. [Hint: The first half of both collisions caused the car to experience the same change in kinetic energy over the same distance.]
Assuming the seatbelt holds the person firmly to the seat so that they always have the same velocity as the car and come to a stop over the same distance (and time). Therefore our model of the forces applies to both the car and the person. To find the forces on the person we would simply use their mass in the equations instead of the car mass.
6) A car with a ridged frame that does not permanently deform will act similarly to a spring, except that the compression happens over a very short distance. Considering that behavior, rank the size of the peak collision force for elastic cars, rigid frame cars, and cars with crumple zones as predicted by our model. Explain your reasoning.
7) Does our model predict that crumple zones are effective at reducing collision forces? Explain.
Real collisions can be more complex than our idealized model. For example, the colliding objects may have similar mass, the case of the elastic collision will not be perfectly elastic, and the crumple zone will likely not produce perfectly constant force. Friction from the bottom of the seat also acts on the occupant. We are assuming the model still captured the overall behavior of each collision type to provide us with the correct ranking of peak forces and the correct conclusion about the effectiveness of crumple zones, but we still want experimental verification.
Collision experiments were performed for a rigid frame, a springy frame, an attempted crumple zone built from soda can aluminum, and finally a crumple zone built from aluminum foil. The velocity of the cart was measured by the cart’s optical sensor and the force on the simulated occupant of the cart was measured with a force sensor. All of the necessary data is available in an online spreadsheet. You can copy and paste the data into your own sheet for analysis.
8) Create a single graph containing plots of the the velocity vs. time data for all 3 trials shown in the datasheet. This will allow you to quality check your data. Make sure you have a complete dataset that includes the maximum speed reached by the cart for each trial. Be sure to name your graph and label the axes, including units. Also be sure to add a legend so you or anyone else can identify which dataset in your plot is which trial.
9) Create a single graph containing plots of the the force vs. time data for all 3 trials shown in the datasheet. This will allow you to quality check your data. Make sure you have a complete dataset that includes the maximum speed reached by the cart for each trial. Be sure to name your graph and add axis labels with correct units. Also be sure to add a legend so you or anyone else can identify which dataset in your plot is which trial.
10) Use the MAX spreadsheet function to find the peak speed for each trial. (The datasheet contains empty rows at the top for you to apply this function). Are the collision speeds for each trial all the same to within a few percent? Show your calculations below.
11) Based on the experimental data, rank the collisions by peak force applied to the occupant, from lowest to highest.
12) Change the scale on the force graph to zoom in on the impulses for the two non-rigid collisions. Describe the shape of the impulses for the spring collision and crumple collision.
13) Did the crumple zone act as designed and provide a (nearly) constant force during the collision?
14) Use the MAX and AVERAGE spreadsheet functions to find the peak force and average force for each trial. (The datasheet contains empty rows at the top for you to apply this function). In the space below, record the peak force and average force for each type of collision.
15) Considering your results, when comparing rigid frames, spring systems, or crumple zones, which is the best safety system?
16) What changes could we make to our experimental methods to reduce uncertainty in our measurements? Provide a detailed explanation. If you suggest new equipment, be sure to including a description of how the equipment would work.
17) What changes could we have made to our experiment to more accurately recreate a real collision between cars?
It might initially seem like building cars to be rigid would be a good idea because the occupants would be “protected” by a cage that would not deform. However, we have shown that a rigid frame actually increases the force on the occupants. It might then seem like an very compressible elastic frame would reduce the force and also prevent permanent damage to the car. However, we have shown that the elastic collision still puts more more force on the occupants than a crumple zone collision. In fact, the elastic collision is even worse than we have found in this case because of the bounce-back. If the car bounces back but the person’s head continues forward due to inertia, then the relative impact speed between their head and the dashboard is amplified by the bouncy collision. The same concept applies to airbags, which are designed with holes to allow deflation as your head hits them, rather than bounce your head back the way a beach-ball would. If airbags were instead elastic, they would increase the peak force on your skull just like the elastic collision for the car, and in addition the impact speed for your brain against your skull would increase because your brain would be moving forward while your skull bounced back. Even if the car hits a less massive object and doesn’t actually bounce back, the elastic collision still increases the change in velocity of the car compared to the dissipative collision, and thus increases the relative impact speed with the dashboard.
Overall, the crumple zone decreases the impact speed between your skull and the airbag while the airbag decreases the impact speed between your brain and skull.
During our experiment we use the motion sensor to measure the bounce-back speed of the cart because the fan was in the way. However, we can use the Impulse-Momentum Theorem to find the change in velocity for the occupant of the vehicle. The larger the change in velocity, the more bouncy the collision was. The cart mass doesn’t change during the collision, so the Impulse Momentum Theorem looks like this: $\bold{F_{ave}}\Delta t = m\bold{\Delta v}$.
18) Solve the impulse momentum theorem for the change in velocity.
19) Find the impulse on the car for each collision by multiplying the average force for each collision by the duration of the collision.(You will notice in the data that all of the collisions have the same duration. Record the impulse values here:
20) The mass of the simulated occupant was 0.05 kg. Calculate the change in velocity for each collision. Show your work.
21) Rank the collisions by the magnitude of change in velocity.
22) Does the result of analyzing the change in velocity add support to our conclusion about the effectiveness of crumple zones, or not? Explain your reasoning.
8
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The following video shows the necessary experiments being performed. The data collected during the experiments seen in the video are contained in an online spreadsheet. Copy and paste the data into your own sheet to perform your own analysis.
If we assume the disk and ring have uniform density we can model their moments of inertia using known formulas.
1) Write the formula for the moment of inertia of a ring.
2) Use the values provided in the video to calculate the moment of inertia of the ring.
3) Write the formula for the moment of inertia of a disk
4) Use the values provided in the video to calculate the moment of inertia of the disk. Show your work.
If we neglect air resistance, friction in the axle of the rotating base, friction in the sensor pulley, and the small moment of inertia of the sensor pulley, then we can model the base, ring, and disk as an isolated system and apply the Law of Conservation of Angular Momentum to the collision.
5) Symbolically write out the Law of Conservation of Angular Momentum applied to the collision. Include the rotating support, disk, and ring in your system. Use the symbols $I_r$, $I_d$, $I_b$ for the moment of inertia of the ring, disk, and base, respectively. Use $\omega_i$ and $\omega_f$ for the initial and final angular velocities.
6) Symbolically solve your conservation equation for the moment of inertia of the base. Show your work.
We can see that our model equation for the moment of inertia of the base requires the angular velocity of the base immediately before and after the collision as inputs.
7) Plot the angular velocity vs. time data for the collision experiment. Be sure to name your graph and label the axes, including units.
8) Find the angular velocity values immediately before (initial) and immediately after the collision (final). Record here:______________________
9) Assuming the rubber belt does not slip, the tangential speeds of the sensor pulley and the apparatus axle must be the same. Symbolically write out the formula for the tangential speed of the sensor pulley in terms of angular speed and pulley radius. Do the same for the support base axle.
10) Set the tangential speeds equal and symbolically solve for angular speed of the base in terms of the angular speed measured by the sensor. Don’t assume that the radius of the pulley and the radius of the base axle are equal.
11) If radius of the base axle and the radius of the pulley were not the same then we would need to measure them so we could use your previous equation to find the true angular velocity of the base from the measured pulley angular velocity. In this case the they are the same, so we can cancel them out of the previous equation. After making that cancellation we find that the angular velocity of the base and the the angular velocity measured by the sensor are _______________.
12) Enter the velocity values and the disk and ring moments of inertia into our model equation solved for the base moment of inertia to find that value. Show your work.
Our model of the collision assumed that friction in the axle of the support was negligible, but at this point we don’t have any evidence to support the validity of that assumption. We will use the rotational form of Newton’s 2nd Law and rotational kinematics to model the effects of friction and air resistance on the velocity and then incorporate that effect into our Angular Momentum model to estimate how the
\begin{equation}
\tau_{net} \Delta t = \Delta L
\end{equation}
If we expand the change in angular momentum we have
\begin{equation}
\tau_{net} \Delta t = L_f -L_i
\end{equation}
The final and initial angular momenta can be calculated from the moments of inertia and the final and initial velocities.
\begin{equation}
\tau_{net} \Delta t = (I_b + I_d + I_r)\omega_f – (I_b + I_d)\omega_i
\end{equation}
We can obtain the collision interval $\Delta t$ from the velocity data, but we don’t know the torque caused by friction and air resistance. However, we can use Newton’s Second Law to replace the frictional torque in the equation. For example, the frictional torque must be equal to the moment of inertia of the base + disk multiplied by the angular acceleration they experience when the system spins down due to friction. $\tau_f = (I_b + I_d)\alpha_f$.
\begin{equation}
(I_b + I_d)\alpha_f \Delta t = (I_b + I_d + I_r)\omega_f – (I_b + I_d)\omega_i
\end{equation}
We can analyze the angular velocity data prior to the collision to determine the angular acceleration caused by friction and air resistance. At that point the only unknown variable in the previous equation will be the moment of inertia of the base.
13) Symbolically solve the previous equation for the moment of inertia of the base. Show your work.
14) Do you expect that your model that ignores friction will produce a higher or lower value for the inertia of the base as compared to the model that does account for friction? Explain your reasoning. [Hint: Think about how friction changes the angular velocity and if that would make it appear as though the base inertia was larger or smaller. Also compare the equations produced by the two models, how would differences in the equations change the result for the base inertia calculation?]
To use the model equation your derived above we need to determine the acceleration of the spinning base +disk under the influence of friction and air resistance, or $\alpha_f$.
15) Plot a the angular velocity vs. time data for the period prior to the collision when the base + disk are spinning down due to friction alone. Be sure to name your graph and label the axes, including units.
16) Fit a line to the data and record the fit equation and R2 value here:
17) Examine the fit equation to determine the acceleration due to friction.[Hint: What part of the velocity vs. time graph represents the acceleration?]
18) Enter the acceleration value into your model equation for the base moment of inertia of the base. Also enter the known moments of inertia for the disk and ring, the measured initial and final collision velocities, and the collision interval. Calculate the moment of inertia of the base.
19) Compare the results of the simplified model and the advanced model. Did the model ignoring friction produce an base inertia value that was larger or smaller than the frictional model in the way that you predicted? Explain.
20) Calculate a percent difference between the output of the two models. Show your work.
21) If we want to maintain 5% accuracy in determining moments of inertia using our experimental setup can we use the simplified model or should we use the more complete model instead?
22) In addition to accounting for friction, what next steps would you take to further improve the collision model (make the collision model more complete)? Explain why the changes would improve the model and how you would determine any new unknown parameters added to the model by your changes.
23) What type of collision did we analyze? [Hint: The objects started separated and then stuck together.]
24) Do you expect kinetic energy to be conserved during this collision? Explain.
25) Calculate the percent change in kinetic energy during the collision. Show your work and work symbolically until the end.
26) Where did the kinetic energy go?
9
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
Materials can be categorized as brittle or ductile based on the relative size of their linear and failure regions. A brittle material will fracture or rupture very shortly after reaching the yield point, the point at which the material begins to permanently deform. A ductile material will have a relatively long failure region, corresponding to permanent deformation without fracture or rupture.
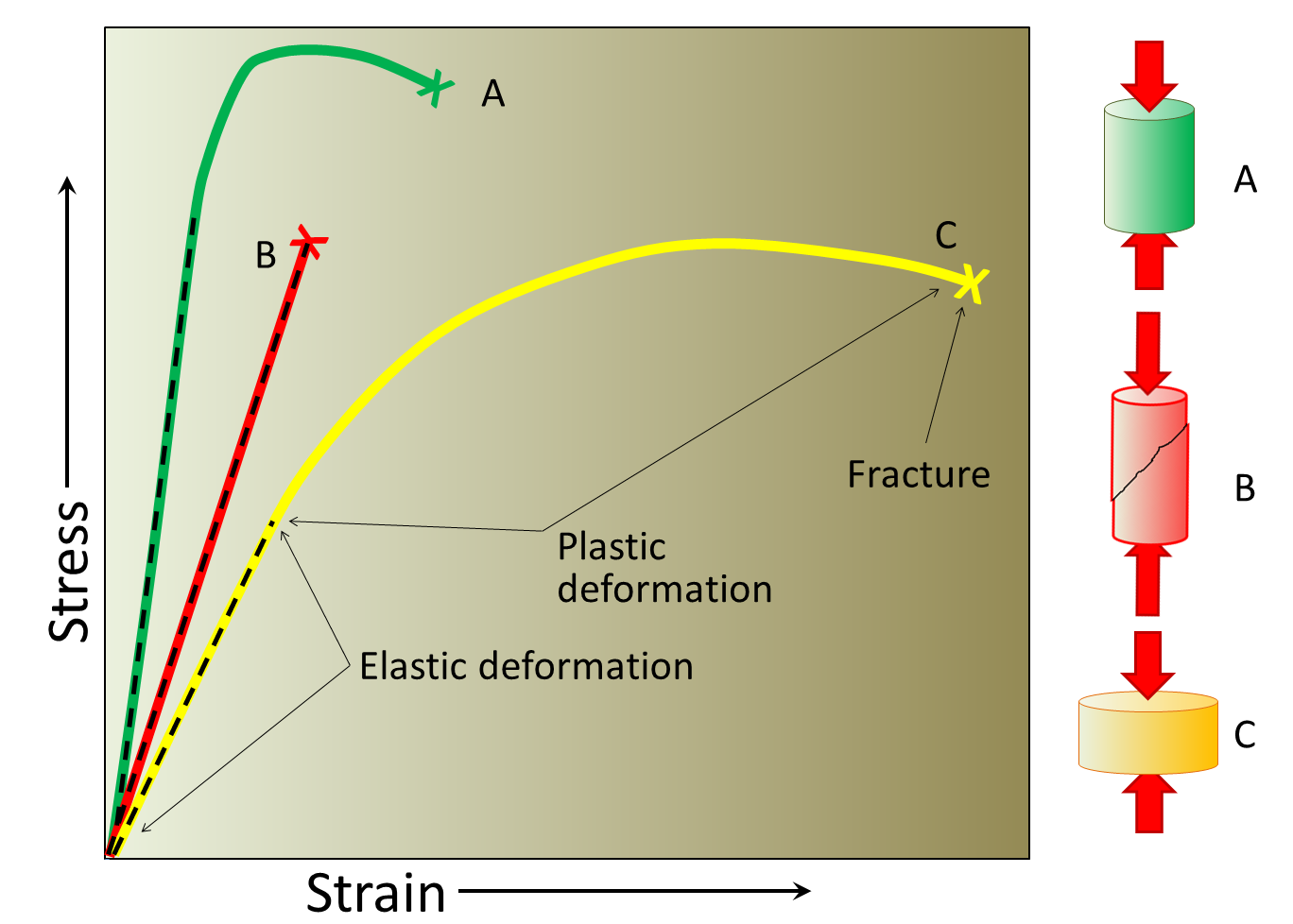
Some materials stretch easily up to a certain point, but then become very stiff and difficult to stretch. This behavior causes a toe region in their stress vs. strain curves. For example, the stress vs. strain curves of tendons exhibit a toe region do to crimping behavior.
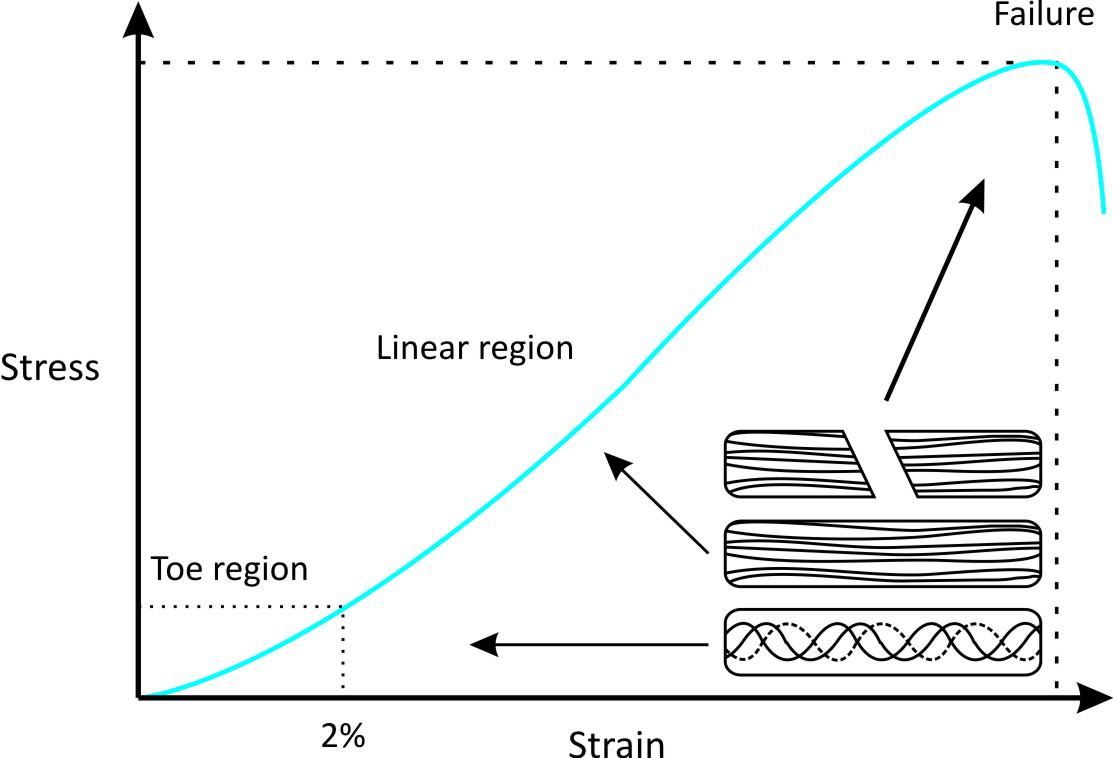
1) We will measure a stress vs. strain curve for a common hair tie to determine if the material comprising the hair tie exhibits a toe region and categorize the material as brittle or ductile. Based on your experience, do you expect that the hair tie will exhibit a toe region? Explain your reasoning.
2) Do you expect that the hair tie material will be brittle or ductile? Explain your reasoning.
We will measure a stress-strain curve for a common hair tie using a strength and materials tester as seen in the following video. The data collected in the video is available in an online spreadsheet. You can copy and paste the data into your own spreadsheet for analysis.

To calculate stress we will need to know the cross-sectional area of the rubber band. We will assume the band does not thin out as it stretches so we will use the original cross section to calculate the stress throughout the experiment. The result of this approximation is known as the engineering stress. If we were to instead measure and use the changing cross-section throughout the experiment we would be calculating the true stress. The original diameter of the hair tie was measured to be 2.4 mm using calipers (see image below).

3) Calculate the cross-sectional area of the hair tie in units of m2. The hair-tie was looped around the quick-links in the materials tester, so we were actually stretching two strands of the hair tie and you need to double your cross-sectional area value to account for that. Show your work.
4) Use your spreadsheet and known original length calculate the strain corresponding to each displacement value.
5) Use your spreadsheet and the cross-section you calculate to calculate the stress corresponding to each force value.
6) Plot the stress on the vertical axis and strain on the horizontal axis. Be sure to title your graph and enter axes labels with correct units.
7) The elastic modulus of the material is defined as the __________ of the graph in the __________ region of the stress vs. strain curve. (Reading your textbook will remind you of how to fill in the blanks).
8) Create a second plot that only contains the data from the region you answered above. Fit a line to this data and record the fit equation and the R2 here:
9) What is the elastic modulus of the hair-tie material?
10) What is the elastic modulus in units of MPa and also in units of GPa?
11) Use your graph or examine your data to find the ultimate strength of the hair tie material. Record the value in units of MPa and also in units of GPa.
12) Does the hair tie stress vs. strain curve contain a toe region, and if so, what strain values does it cover? Explain.
13) Is the hair tie material brittle or ductile? Explain your reasoning.
14) Overall, does the hair tie behave according to your original expectations? Explain.
15) The uncrimping (toe region) of a tendon provides flexibility by allowing the tendon to stretch to occur under small stress and without significant strain to the actual material fibers themselves. Once the tendon fibers are uncrimped the tendon becomes very stiff to provide stability while the muscles to apply large forces to skeletal system (steep linear region). Tendons are typically relatively brittle, as indicated by rupture soon after failure begins (sharp drop in stress after the yield point). Are hair ties good qualitative models for tendons (do they behave the same)?
16) How does the elastic modulus of the hair tie compare to the elastic modulus of a tendon? Provide a ratio of the two values. Also properly cite your source for the tendon value.
17) How does the ultimate strength of the hair tie compare to the ultimate strength of a tendon? Provide a ratio of the two values. Also properly cite your source for the tendon value.
18) Overall, does the hair tie make a good model for a tendon? Explain.
19) Both tendons and the hair tie exhibit a toe region because the fibers of the material must be uncrimped and aligned before actually being stretched. Use the concepts covered in this lab to explain why you think it might be advantageous to have a toe region in the stress vs. strain graph of a hair tie.
The work done on the hair tie before it breaks is equal to the area under the measured force vs. displacement curve. We can approximate the force vs. displacement area by multiplying each little bit of additional displacement by the average force recorded during that additional displacement and then adding up all of these results. This process, known as numeric integration, essentially breaks the curve into many small rectangles, finds the area of each little rectangle, and adds up all the little areas.
20) Let’s try this with our hair tie. Use your spreadsheet to average the first two force values in the second cell of the new column. Subtract the first displacement from the second in order to find the displacement over which that average force was applied. Continue this pattern for all the force and displacement values until fracture occurred. Make a third column that converts the additional displacement to meters and multiplies by the average force. This will be the work in Joules. The following chart shows an example of what you are trying to create, with made up example values for displacement and force.
| Displacement (cm) | Force (N) | Average Force (N) | Additional Displacement (cm) | Work (J) |
| 0 | 0 | |||
| 0.2 | 1 | 0.5 | 0.2 | 0.001 |
| 0.3 | 2 | 1.5 | .1 | .0015 |
| 0.5 | 4 | 3 | 0.2 | 0.0006 |
21) Use your spreadsheet to sum up each little work done to get the total work before rupture. Record here:
22) If you attached a hook to the hair tie and used it to catch a moving object with mass of 0.5kg, how fast could the object be moving without breaking the hair tie? [Hint: To stop the object the hair tie must do an amount of work that is equal to the object’s kinetic energy.]
23) From how high would you drop an object in order for it to reach the speed you calculated above?
In similar fashion, there are limits on how much energy can be transferred to your tendons when pushing off to change direction or landing after a fall.
10
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
We will determine the density of a potato using mass found from a scale and volume found two different ways and then compare those results. Finally we will determined using hydrostatic weighing, which does not require a direct volume measurement and compare those results as well. The following video shows the necessary data being collected.
[Outcome 4-1]
1) Record the potato mass provided by the scale (in units of grams):__________g
2) Record the potato circumference (in units of cm): __________cm
3) Look up a formula that relates the volume of a sphere to it’s circumference. Record the formula below and cite your source (provide a citation that includes a full URL, not just a website name.)
4) Model the potato as a sphere to estimate the volume of the potato and be sure to include correct units in your answer. Show your work.
5) Use the mass and volume to calculate the potato density, be sure to include correct units in your answer. (You may need to look up how density is defined by mass and volume.) Cite your source and show your work.
[Outcome 4-1]
6) Record the volume of water displaced by the potato when fully submerged:___________ cm3. Assuming there are no trapped air bubbles, the fully submerged displaced volume is same as the volume of the potato.
[Outcome 4-4]
7) Calculate the potato density from the mass reading on the scale and the volume determined by displacement. Show your work.
8) How do the results from the previous two methods of determining density compare? Calculate a % difference between the two results. Show your work.
9) Which result do you trust more? Explain your reasoning in detail. [Hint: Your reasoning should involve a comparison of the sources and sizes uncertainties in the measurements used for each method.]
The hydrostatic method allows us to reduce uncertainty in measuring the density of objects with complex shapes by eliminating the need for a direct volume measurement. Instead we apply Archimedes’ Principle and the concept of static equilibrium to calculate the volume from measurements of the weight and apparent weight.
10) Record the weight of the potato in air (use units of Newtons) :___________N
11) Record the weight of the fully submerged potato here:___________N. This is known as the the apparent weight because the object appears to weigh less when it is submerged. In hydrostatic weighing applications, the apparent weight is sometimes called the under-water weight.
12) Based on your measured weight and apparent weight, what must be the size of the buoyant force that pushes up on the submerged potato? [Hint: The object is not moving, so it must be in static equilibrium. Draw a free body diagram of the potato to help you answer this question, but don’t forget to include the upward force from the hook attached to the scale].
13) Write Archimedes principle. [Hint: It tells you how the buoyant force on an object relates to the weight of fluid displaced by the object.]
14) You have already found the buoyant force using static equilibrium, so now apply Archimedes principle to find the weight of the water displaced by the object. Explain. Your reasoning.
15) Use the weight of the displaced water to calculate the mass of the water displaced. Show your work.[Hint: How are mass and weight related for an object near the surface of the Earth?]
16) Convert your mass to grams:
17) Look up the density of water in units of g/cm3 and record here:________
19) Now use the density of water you looked up and the mass of the water displaced by the object to find the volume of the water displaced by the object. You may need to rearrange the density formula. Show your work.
You have now found the volume of water that was displaced by the fully submerged potato, and therefore the volume of the potato. Notice that with the hydrostatic method we found the volume of the potato from measurements of weight and apparent weight and the known water density, but we didn’t attempt to measure the potato volume directly. Now you know the volume of the potato, so you just need to know its mass to calculate it’s density.
20) Use the weight that you found at the start of the hydrostatic method to calculate the mass in kg. [Hint: How are mass and weight related for an object near the surface of the Earth?]
21) Convert the potato mass you found above to grams.
22) Now use the the above potato mass (in g) and volume in (in cm3) to calculate the potato density. Show your work.
23) How do the results from the hydrostatic method and the other two methods compare? Calculate a % difference between each set of results. Show your work.
24) Which result do you trust more? Explain your reasoning in detail. [Hint: Your reasoning should involve a comparison of the sources and sizes uncertainties in the measurements used for each method.]
Even for objects with complex shapes we can measure mass on a scale and finding volume from a displacement measurement, like we did in the second experiment (displacement method), so it might appear that the hydrostatic method does not provide any additional advantage. However, measuring the volume of large objects can be difficult and error prone compared to the hydrostatic method. To illustrate this issue we will examine hydrostatic method for determination of body density, which is often used for the purpose of estimating body fat percentage. The following video illustrates the procedure.
To use the displacement method instead of the hydrostatic method you would need to submerge a person, have them expel the air from their lungs, and the wait while the surface of the water settled down so that you could mark it and measure the displacement. Notice how much the surface is moving due to the bubbles and movement of the person. The person would probably not be able to hold their breath that long enough to allow the water to fully settle down. Spread out over the entire water surface, even a half centimeter error in measuring water line would add significant error to the volume measurement. Let’s examine that error.
25) If the tub is 100 cm wide by 150cm long, similar to the one in the video, what volume error would result from a 0.5 cm error in the water line?
26) To estimate a percent error in body volume we need the average volume of a person. The average mass of people is about 60 kg and the average density is very near that of water. Use that information and the definition of density to estimate the average volume of a person in cubic centimeters. Show your work.
27) What would be the % error in body volume caused by the error in reading the water line?
That same error would propagate to the density calculation. That is why the hydrostatic method is favored over the displacement method.
The hydrostatic method eliminates uncertainty associated with the water line measurement, but not the uncertainty associated with estimating the residual lung volume, which would also need be done with the displacement method. For people, residual volume can be estimated from empirical models that depend on age, height, and gender, as seen in the diagram below. Once density is determined from the hydrostatic method, using an empirical model that requires body density, $D_b$, as an input. The model looks like this (using under water weight to mean the same thing as apparent weight).
The work you did in the hydrostatic weighing part of this lab was a stepwise recreation of the equation for calculating body density $D_{b}$ that is shown in the diagram above, except for the part about residual volume of body gasses ($RV$) because our potato didn’t have lungs or intestines.
28) For fun we will use the potato density we found using the hydrostatic method as an input to calculate the “body fat percentage” of our potato, just as we would for a person. Follow through with that calculation of body fat percentage using the Siri Equation seen in the above diagram. Use the density value you found in units of grams/cm3. Show your work.
29) Is the BF% value your found meaningful? Explain.
Be careful when applying any model to a system it wasn’t meant to describe (a model for humans applied to a potato). Just because it will give you a result, that doesn’t mean the result is meaningful!
11
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The simple pendulum model predicts that the pendulum will behave as a simple harmonic oscillator with the angle of the string away from vertical serving as the displacement. The oscillator frequency will depend only on the length of the pendulum (L) and the gravitational acceleration (g) according to the following equation, which we will put to the test in this lab.
$ f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}$
The simple pendulum model is derived under the following assumptions:
1) Determine the angle in radians above which the small angle approximation has more than 1% error. (At what angle does the percent difference between $sin\Theta$ and $\Theta$ become more than 1%).
2) According to the simple pendulum model, the the oscillation frequency depends on the string length to what power? (Length is raised to what power in the frequency equation at the start of the lab?) Note that no dependence on length means a power of zero. Explain.
3) According to the simple pendulum model, the the oscillation frequency depends on the mass to what power? Explain.
4) According to the simple pendulum model, the the oscillation frequency depends on the oscillation amplitude to what power? (Meaning amplitude is raised to what power in the frequency equation?) Explain.
We will test the simple pendulum model by verifying that it correctly predicts how the oscillation frequency on length, mass, and amplitude.
5) As you found above, the model is only valid for amplitudes less than _____radians or, equivalently, ______degrees. For the purpose of this lab we will call that angle $\Theta_1$. Hang your pendulum and release it from an amplitude less than $\Theta_1$ and use a stopwatch to time 10 full oscillations. Record your data below.
Object:__________
Starting amplitude:__________
Time for 10 Oscillations:__________
6) Use your time for 10 oscillations to calculate the oscillation period, frequency, and angular frequency. Show your work.
7) Repeat the experiment for every amplitude from 2 degrees up to $\Theta_1$ at 2 degree intervals. Record your results in a spreadsheet and use the spreadsheet to efficiently calculate the period and frequency for each case.
8) Make a graph of the oscillation frequency vs. amplitude. Be sure to label the graph and the axes, including units.
9) Apply a best fit line and record the fit function and R2 value here. Does the frequency appear to depend on amplitude? Explain.
10) With regard to the dependence of oscillation frequency on amplitude, does the data support the validity of the frequency equation predicted by the simple pendulum model? Explain.
11) Shorten the string by about 10% and choose an amplitude less than $\Theta_1$. Repeat the procedure find the oscillation frequency by timing 10 oscillations at least 6 more times, shortening the string by a bit each time. Record the string length and oscillation frequency in your spreadsheet. (Do not repeat the amplitude test for each string length). Be sure to measure pendulum length from the rotation point all the way to the center of mass of the object, not just the string length!
12) Make a graph of oscillation frequency vs. length. Make sure that your length data has units of meters. Be sure to label the graph and the axes, including units. Copy and paste your frequency and length data into two new columns of the online spreadsheet.
13) Apply a power law fit to data in the graph of frequency vs. length. Record the fit equation and
R2 value here:
14) Does the power law model provide a good fit to your data? Explain.
15) According to your fit equation, what is the power on the length variable? Does this agree with the power dependence predicted by the model? [Hint: You plotted frequency vs. length, so “y” in your fit equation is actually “f” and “x” in your equation is actually “L”. Compare the power of x in the fit equation to the power of L in the frequency equation for a simple pendulum]
16) Compare your fit equation to the simple pendulum equation. Rewriting your fit equation, but replacing “y” with “f” and “x” with “L” will help you remember what the variables in the fit equation mean. If you then write the simple pendulum frequency equation directly below that, you can directly compare each part of each equation. The fit equation indicates that frequency is equal to a coefficient (just a number) multiplied by the length raised to some power. The simple pendulum equation predicts that the frequency is equal to a combination of constants multiplied by the length raised to a power (-1/2). Therefore, if the fit is good, then the combination of constant in the pendulum equation should be equal to the coefficient in the fit equation. Set these equal and solve for g, and calculate a numerical value.
17) Applying a simple pendulum model to your data has allowed you to extract a value for the free-fall acceleration due to gravity on the surface of Earth without having to actually drop anything in free-fall. Of course your pendulum wasn’t really a perfect simple pendulum, and there is uncertainty in your measurements, both of which lead to error. Compare the value for g that you found with the accepted value for g. Show your work in calculating a % difference.
18) With regard to the dependence of oscillation frequency on length, does the data support the validity of the the simple pendulum model? Explain.
To provide experimental data on a variety of masses we will combine all of the class data. Your chosen objects will have a variety of masses. If the oscillation frequency is independent of mass and amplitude, as predicted by the simple pendulum model, then we should be able to fit all of the frequency vs. length data with a single equation.
19) Copy and paste the data from your classmates into the frequency and length columns of your own sheet to create one combined dataset. Make a new graph of this data. Be sure to label the graph and the axes, including units.
20) Apply a power fit to the class data. Record the fit equation and R2 here:
21) With respect to mass, does the class data support the validity of the simple pendulum model? Explain.
22) Overall, do you conclude that the simple pendulum model is valid under the conditions tested by you and your classmates? Explain in terms of the results of each set of analyses you performed.
23) What changes to the experiment would you make to ensure that the experimental conditions more closely matched the assumptions of the simple pendulum model? Explain the reasoning behind your proposed changes.
24) The simple pendulum model predicts that the pendulum will behave as a simple harmonic oscillator, which means the pendulum motion can be described by cosine or sine functions and that the amplitude is constant. However, you observed that the amplitude was not constant–the amplitude decreased over time. Explain what caused the decrease.
In some cases the damping force is proportional to the velocity of the oscillator:
$F_d = -bv$
In that special case, the amplitude will decay exponentially and the decay constant will depend on the damping constant, $b$, that defines the strength of the damping force:
$A(t) = A_0e^{-\frac{b}{2}t}$
Let’s find out if the amplitude of a pendulum can be modeled using an exponential decay, in which case the damping forces acting on the pendulum have the form $F_d = -bv$. The following video shows a pendulum swinging.
25) Label two new with columns with amplitude and time, including units. Watch the video and record the starting amplitude for time zero in your spreadsheet. Next, record the stopwatch time and amplitude on every 5th oscillation until about 1 minute. After one minute the amplitude changes slowly enough that can begin recording the time and amplitude on every 10th oscillation. For each data point you will likely need to use the pause, scrub, and playback speed features of the video player to narrow down when the amplitude fist appeared to drop by a full 0.5 degrees. The playback speed can be adjusted by clicking on the gear in the lower right of the player.
26) Plot the amplitude vs time, name and label the graph, and apply an exponential fit. Record the equation and R2 value here:
27) Do the data suggest that the damping forces acting on the pendulum are proportional to the velocity? Explain.
12
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The following video shows a Vinycombe wave machine used to create travelling pulses, travelling waves, and standing waves. We will extract data from the video for further analysis. Watch the video before continuing with the lab.
1) The section of the video on positive pulses (near 1:16) shows the pulses travel from one side of the machine to the other in real time. Assume the wave machine is 2m long and that the video is being played at real speed. Use a stopwatch to measure the time for a pulse to travel across the machine and then calculate the pulse speed. Reduce uncertainty by playing the video at 0.25 speed while you time, and then multiplying the time by 0.25. Record your values and show your work below. (The playback speed settings can be accessed by clicking the gear icon in the lower right of the player window).
2) The section on travelling waves (near 3:25) shows a traveling wave. Time the oscillations of the hand used to generate the wave to determine the wave frequency. Again, reduce uncertainty by reducing playback speed. Record your values and show your work below.
3) Use the section when the traveling wave is frozen to calculate the wavelength. (You will need to use the known 2m length of the machine to find a conversion between actual distance in meters and distance measured on the screen you are using to watch the video). Record your values and show your work below.
4) From the frequency and wavelength data, calculate the expected wave speed. Show your work.
5) Do the pulse speed and the travelling wave speed appear to be the same? Calculate a percent difference.
6) Use your distance conversion factor to determine the amplitude of the wave. Show your work.
7) Write the complete traveling wave function for this wave, with numerical values for amplitude, angular frequency, and wavenumber. Show any work you to find these values.
8) The bars on the ends of the wave machine are free to oscillate and will form antinodes. The first resonant mode would have one node directly in the middle and antinodes directly on the ends. Draw a picture of such a standing a wave formed in the machine at a moment in time.
9) In terms of the machine length, L, what is the wavelength of the first resonant mode?
10) What is the first resonant frequency? Show your work. (Hint: You already know the wave speed.)
11) The second resonant mode will have two nodes, still with anti nodes at the ends. Draw a picture of such a standing a wave formed in the machine at a moment in time. What is the wavelength of this resonant mode?
12) What is the second resonant frequency? Show your work.
13) As you can see, this machine will support resonant modes that correspond to all harmonics of the first resonant frequency, just like a system that is fixed on both ends (as opposed to a system only fixed on one end that only supports odd harmonics). Write a function for the nth resonant frequencies of this machine in terms of the wave speed, machine length, and n.
14) Time the oscillations of the hand generating the waves that form standing waves (near 3:45). Determine the driving frequency. Record your values and show your work.
15) Is the driving frequency near one of the resonant frequencies? Which resonant frequency is nearest?
16) How many nodes should be present in the standing wave mode associated with the resonant frequency you found above, and what should the distance between them be? Explain/show your work. [Hint: Re-examine the pictures of the first few resonant modes to look for a pattern in number of nodes vs. resonant mode).
17) Use the video to determine the actual number of nodes and the distance between them. (You will need to use the known 2m length of the machine to find a conversion between actual distance in meters and distance measured on the screen you are using to watch the video). Record your values and show your work below.
18) How does the standing wave mode (number of nodes and distance between them) compare to the mode predicted from the resonant frequency (in 16)?
19) Overall, does the free-ends model do well at describing the spatial behavior of this standing wave resonant modes?
Standing waves are an example of a spatial interference pattern (the amplitude of oscillation changes across different locations in space, but the amplitude at those locations is constant in time). Beats are an example of a temporal interference pattern (the amplitude of oscillation at one location will change in time).
You can hear beats when you listen to two soundwaves of similar frequency (listening for and minimizing the beat frequency is how instruments are tuned). We will visualize the continuous arrival of two waves of different frequencies at a certain location in space. To do that, we simply need to calculate the displacement of the two waves at each point in time and apply the superposition principle to determine the resulting amplitude at each point in time.
20) Create a spreadsheet with time values in the first column running from 0 to 200 in increments of 1. In the second column calculate the displacement of a traveling wave at each time with period of 10 and amplitude of 5. Choose the current location of the wave as x = 0 so that the oscillation at that point can be described by $Asin(\frac{2\pi}{T}t)$ for A = 5, T = 10.
21) Plot the displacement vs. time for this location. Choose a plot type that connects the points so you can visualize the signal. Be sure to title your graph and label the axes (we haven’t specified any units for time or displacement, so write “arb. units”, which is short for arbitrary units).
22) In the third column repeat the procedure for a wave with A = 5, T = 9. ($Asin(\frac{2\pi}{T}t)$ for A = 5, T = 10).
23) Calculate the frequencies of these two waves and their expected beat frequency? Show your work.
24) Make a fourth column that is the superposition of the first two waves to determine the resulting displacement at this location where the waves meet.
25) Make a whole new plot of the resulting displacement vs. time for this location. Choose a plot type that connects the points so you can visualize the resulting signal. Be sure to title your graph and label the axes (we haven’t specified any units for time or displacement, so write “arb. units”, which is short for arbitrary units).
26) Using the new graph, determine the period of the resulting wave envelope as the time from one peak to another and record below. This is the beat period you would hear if these were two sound waves.
27) Use the beat period to calculate the beat frequency. Show your work.
28) How does the beat frequency compare to the expected beat frequency?
13
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
We will build a program to simulate the distribution of energy among the atoms in two ideal gasses that are in separate containers but able to exchange thermal energy. For example, the container walls are in contact to allow conduction and/or the container walls are clear to allow exchange of radiation. Though there are more efficient methods, we will build our simulation with a spreadsheet because previous labs have allowed us to become familiar with using spreadsheets. We will use a random number generator to simulate a random physical process, so this type of simulation is known as a Monte Carlo simulation (named after the famous casino).
1) Which macrostate had the highest predicted multiplicity (and therefore probability)?
2) Based on your multiplicity calculations, are there more ways (microstates) to distribute thermal energy evenly throughout a system, or are there more microstates that produce higher concentrations of energy in parts of the system? Explain.
3) The probability of different macrostates (total energy in each gas) depends on their multiplicity. Due to your answer above, are the most probable macrostates those with well distributed energy, or poorly distributed energy? Explain.
4) Entropy is a measure of how well the thermal energy is distributed throughout a system (more distributed means higher entropy). Based on your answers above, should the most likely macrostates of a system will have relatively high entropy or low entropy?
5) Does your previous answer agree with the Second Law of Thermodynamics, which says that the entropy of an isolated system should always increase due to spontaneous processes? [Statistically, a system that starts in low probability microstate is likely to end up in a higher probability microstate. Based on our analysis so far, would that mean about the entropy change?] Explain your reasoning.
6) Do your previous answers agree with the entropy calculated directly from the multilplicity as in the simulation spreadsheet? (e.g. is the highest probability macrostate also the one with highest entropy?)
7) We know that two systems allowed to spontaneously exchange heat will trend toward thermal equilibrium. In order for that observation to align with our analysis so far, the macrostate with the highest probability (and highest entropy), has to be one that puts the two gases in thermal equilibrium. Is this the case according to your temperature calculations for each gas? What is the predicted equilibrium temperature of this gas?
Overall, we are interpreting thermal equilibrium and the Second Law of Thermodynamics as simply consequences of basic statistics. In systems with many atoms storing many units of energy, the statistical probability of increasing entropy becomes so large compared to the probability of decreasing entropy that we just don’t observe spontaneous decreases in entropy over everyday timescales. Let’s run our simulator to see if the simulated data support that interpretation, with the understanding that we will only simulate 10 atoms with 10 units of energy and we will only run 200 trials.
8) Run the simulation for 200 trials.
9) Plot the simulated probability vs. macrostate (number of energy units in gas A). This is known as a probability distribution. Be sure to give your graph a title and axis labels.
10) Add a second series to the same graph. The second series will plot the predicted probability vs. macrostate.
11)Does the probability distribution produced by the simulation agree with the distribution predicted by the two-state model? If not, explain how they differ and explain why do you think they did not agree.
12) What is the macrostate with the highest frequency (state in which the system spent most of it’s time)?
13) What is the macrostate with the highest frequency (state in which the system spent the least of it’s time)?
14) Does the highest frequency macrostate agree with your predictions? Explain.
15) When there is an unequal number of atoms in each gas then there is not an equal probability of each energy unit ending up in either gas. There is a higher probability that it ends up in the gas with more atoms. Therefore, we can’t use the two-state model to predict the probabilities of each macrostate. However, based the connections between probability, entropy, and thermal equilibrium that we made at the beginning of lab, we do expect that expect that the most likely macrostate is the one which places the two gases in thermal equilibrium. Change the atom numbers in your spreadsheet to 3 in gas A and 7 in gas B. Looking at your temperature values for the two gases. Which macrostate (energy in each gas) would place the system in thermal equilibrium and what would the equilibrium temperature be?
16) Run the simulation for another 200 trials with the atom number set to 3 in gas A and 7 in gas B.
17) Does the simulated data agree with your prediction for the most likely macrostate and equilibrium temperature? Explain any differences.
18) Overall, do the calculations support the prediction that temperature is the quantity which will be equal for the maximum entropy state, as opposed to other quantities such as volume, etc? [Hint: Is the state with equal volumes the one with maximum probability, or the state with equal temperature?] Explain.
19) Does it appear that the simulation is useful for visualizing and predicting the probability distribution for the macrostates and corresponding state variable values of a monatomic ideal gas? Explain.
20) We only simulated a few units of energy distributed among a few atoms. Even when we aren’t manually tallying the frequency as we did in this case, we find that scaling microscopic simulations to macroscopic systems is computationally prohibitive. For example, if you were to simulate just one liter of gas at room temperature (300 K), and atmospheric pressure, how many atoms would we need to simulate? Show your work.
20) What is the average kinetic energy of each atom in this 1 liter of gas?
21) Using the same energy unit size as in our simulation, how many energy units would each atom have on average?
22) In that case, how many energy units would we need track in order simulate this liter of room temperature gas?
14
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The video below shows the methods used to warm a piece of metal in a hot water bath and then transfer the metal to a Styrofoam cup filled with water inside a calorimeter. The Styrofoam cup provides insulation, and the cup itself is suspended within an aluminum cylinder with a layer of air between to provide additional insulation. The shiny metal cylinder also reduces radiative exchange of thermal energy. The cylinder itself is then suspended within a larger metal shell, once again separated by a layer of insulating air. A lid prevents significant convection or evaporation, but does have a hole to allow insertion of of a thermometer to monitor the contents of the calorimeter. Due to the hold in the lid, the calorimeter is an open system. If we assume the hole is sufficiently small that there is negligible exchange of particles in/out of the calorimeter then we can treat the contents as a ___________ system. If we also assume that the insulation is essentially perfect and the heat transfer in/out of the calorimeter is negligible then we can treat the contents as an _____________ system.
1) Modeling the metal and the water inside the calorimeter as an isolated system allows us to set the net thermal energy transfer (heat) of the system to zero. Therefore, the heat gained by the water must equal the heat lost by the metal. Using this model, symbolically derive an equation for the specific heat of the metal ($c_m$). Your result should depend on the following variables that are seen in the video: mass of metal ($m_m$), initial metal temperature ($T_m$), specific heat of water ($c_w$), mass of water ($m_w$), initial water temperature ($T_w$), and final temperature of the combination ($T_f$). Show all of your work:
2) Enter the values from the video into your model for the metal specific heat and calculate a value. Show you work.
3) Look at this table of specific heat values and compare your value to those listed to identify the metal in this experiment. List the value of the metal you chose from the list and calculate a % difference from the value found in this experiment.
4) List some possible sources of uncertainty in our determination of the specific heat value that were related to the experimental methods and measurement tools, but not caused by mistakes in calculations.
5) Our model neglected any temperature change by the Styrofam cup in the calorimeter. Now include the Styrofoam cup in the model and recalculate the specific heat value of the metal. Assume the initial and final temperatures of the Styrofoam were the same as the water it contained. Look up a value for Styrofoam specific heat capacity from a reliable source and provide a full URL for your source. Show all work.
6) How much did the determined specific heat value change when accounting for heating of the Styrofoam cup, and did it increase or decrease? Calculate a % difference between the two values produced by the two models.
7) Did accounting for this effect bring the specific heat value closer to a different metal the the one you identified previously? Explain. Does it appear to be necessary to include the Styrofoam cup in the analysis for this type of experiment? Explain your reasoning.
Our analysis methods neglected any cooling of the metal during the transfer from the hot water bath to the calorimeter. The following infrared images indicate that the metal is radiating and that air surrounding the metal is undergoing natural convection (which implies that the air is first warmed by conduction from the metal).


To estimate how much cooling may have occurred, another experiment was performed. The metal was once again removed from the hot water bath and it’s temperature was measured and recorded by an infrared thermometer as seen in the following video.
8) How much did the temperature of the metal change during three seconds in the air just after being removed from the hot water bath?
9) Assume the same temperature change occurred for the metal in the original calorimetry experiment and that the metal was actually that much colder than you originally thought. Recalculate the metal specific heat with the expected lower initial temperature value. Show all work.
10) How much did the determined specific heat value change when accounting for cooling of the metal during transfer, and did it increase or decrease? Calculate a % difference between the two values produced by the two models.
11) Did accounting for this effect bring the specific heat value closer to a different metal than the one you identified previously? Explain. Does it appear necessary to be concerned about the heat loss during transfer to the calorimeter for this type of experiment? Explain your reasoning. (Consider the error in determining specific heat that you discovered was caused by these effects and compared to the difference in specific heat between metals).
12) The metal used in the experiment was actually zink. Was that the metal you identified?
13) Calculate a % difference between the final experimental specific heat capacity of the metal and the tabulated value for zink (look it up and provide a citation for your source).
15
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The electroscope is designed to indicate the presence of charged objects. The following video shows a series of electroscope charging experiments being performed. As seen in the following video, the electroscope used in for this lab consists of a flat metal plate directly connected to a vertical metal cradle that holds a metal needle that is free to rotate. These conducting components are insulated from the metal frame by two plastic washers. The conducting components can be grounded by touching the plate with a grounding rod or simply with you hand.
The Laws of Physics aren’t different from one time to the next, or from one location to the next. Therefore, each of our explanations for the behaviors seen in the video must be consistent with one another and with our fundamental understanding of electric charge:
1) In the first experiment a balloon was rubbed on a shirt and becomes charged according to a process known as tr____electric charging. Examining the relative electron affinity of rubber and cotton (you may need to look this up), we can assume the balloon acquires a __________ charge.
2) When the charged balloon is brought near the electroscope we see the needle move away from the cradle on both ends. Draw a basic diagram of the electroscope and balloon that indicates any charge on the balloon and any induced charge on the plate, cradle and needle. Use your diagram to support a written explanation for why the needle moves away from the cradle when the balloon is brought nearby. Be sure to cite any and all sources used. [Hint: no net charge was added to the electroscope, but individual parts of the electroscope did become temporarily charged due to movement of free electrons in the metal parts.]
3) The temporary charging of the electroscope parts you described above is called charging by ____________. (Provide citation below.)
4) The second experiment in the video shows the balloon rubbed on the plate of the electroscope. When the balloon is removed the we see that the needle remains separated from the cradle. What type of charge is left on the balloon? What type of charge is left on the plate? [Hint: You will need to look up where a balloons and aluminum fall in a triboelectric series]. Be sure to cite any and all sources used.
5) Draw a basic diagram of the electroscope and balloon that indicates any charge on the balloon and any induced charge on the plate, cradle and needle. Use your diagram to support a written explanation for why the needle stays away from the cradle when the balloon is brought nearby. Be sure to cite any and all sources used.
6) The third experiment in the video shows a neutral metal pie pan brought near the electroscope after it has been charged as described above. We see that the separation of the needle and cradle decreases, as the pie pan nears and increases again as the pan is removed. Draw a basic diagram of the electroscope and balloon that indicates any charge on the balloon and any induced charge on the plate, cradle and needle. Use your diagram to support a written explanation for why the needle moved back toward the cradle when the neutral pie pan is brought nearby. Be sure to cite any and all sources used.
7) The fourth experiment in the video shows a charged balloon brought near the electroscope while it has been grounded (by touching the plate). We see that needle does not initially move as it did in the first experiment when the electroscope was not grounded. Explain why. Be sure to cite any and all sources used.
8) Continuing in the fourth experiment, the electroscope is ungrounded while the charged balloon is still nearby and then the balloon is removed. We see that the electroscope needle remains separated from the cradle. Draw a basic diagram of the electroscope and balloon that indicates any charge on the balloon and any induced charge on the plate, cradle and needle. Use your diagram to support a written explanation for how the electroscope acquired a charge in this case. Be sure to cite any and all sources used.
9) The charging of the electroscope as you described above is called charging by ____________. (Provide citation below.)
Our modeling of the electroscope behavior was based on very basic concepts, so we should be able to apply those same concepts to model the electrostatic behavior of other systems, such as the Van de Graff Generator and pie plates seen in the fifth experiment. The Van de Graff Generator builds up a large net charge on the dome. You can watch the video below to see how:
10) Draw a basic diagram of the Van de Graff Generator dome and pie plates that indicates any charge on the dome and plates. Use your diagram to support a written explanation for the behavior of the pie plates. Be sure to cite any and all sources used.
16
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
In this lab you will determine the maximum charge and voltage on a Van de Graaff Generator. The first video below shows a Van de Graaff Generator in use and the second video illustrates how the generator works.
The build up of charge on the Van de Graaff dome is limited by carona discharge. The following video discusses carona discharge and arc discharge.
As seen in the video above, carona discharge will occur when molecules in the air become ionized. The electric field required to ionize a particular substance is known as the dielectric strength. The dielectric strength of air is $3\times 10^6 \,\bold{V/m}$ "OpenStax College Physics" by Paul Peter Urone, Roger Hinrichs, Capacitors and Dielectrics, OpenStax College Physics is licensed under CC BY 4.0 so we know that the maximum charge that can occur on the Van de Graaff is that amount which produces an electric field of $3\times 10^6 \,\bold{V/m}$.
We will model the Van de Graaff Generator dome as a spherical conducting shell and then find the charge on the shell that would be needed to produce an electric field of $3\times 10^6 \,\bold{V/m}$. The following video shows how to use Guass’s Law to find the electric field on the outside of a charged metal shell. We will use the same equations, but solve for the charge. Watching roughly the first 5:20 of the video will help prepare you for this part of the lab (after that they enter specific values from their problem that are not relevant to us).
1) What is the electric field within the cavity of a charged spherical metal shell?
2) What is the electric field within the metal shell itself?
3) Applying Guass’s Law to the charged spherical shell shows us that on the surface of the shell and beyond we can compute the electric field with what the formula for the electric field of what type of charge? Write that formula below, using the following symbols: $q$ for the charg, $k$ for Coulomb’s constant, and $r$ for the distance from the center of the sphere. Show your work.
4) According to the answers above, where will the electric field be the largest? Explain.
5) Rearrange the formula for the electric field outside of the charged sphere to solve for the charge, $q$. Show your work.
6) Enter the dielectric strength of air for the electric field and the answer to (4) for the radius and calculate a value for the maximum charge that can build up before carona discharge. Show your work.
7) We know that outside the sphere the electric field behaves exactly as though the sphere were actually point charge. Therefore, we know that the electric potential (voltage relative to zero) at the surface of the sphere must be the same as if the sphere were a point charge. Enter the maximum charge and the radius of the sphere into the equation for the electric potential due to a point charge to calculate the electrical potential at the surface of the sphere. Show your work.
Note that the electric potential at a point is defined as the electric potential difference, or voltage, between the point and another location where the potential is defined to be zero, such as on a grounded conductor (or at a distance of infinity). Therefore, the maximum electric potential you calculated above is the same thing as the voltage relative to ground.
As usual, we want to test our theoretical prediction against some experimental results. The maximum distance (gap) at which the Van de Graaff would arc to the grounding rod provides the data we need. The voltage between two electrodes at which the insulating property of the air will break down and allow an arc form between them is known as the breakdown voltage $V_B$. Finding the maximum arc gap will allow us to determine the maximum voltage between the dome and the grounding rod.
Let’s remember that the voltage between two electrodes tells us the amount of kinetic energy per charge that a particle would gain while accelerated across the gap by the electric field between them. Not surprisingly, for large gap distances (or higher gas pressure) a greater voltage is required to achieve an arc discharge because many collisions between electrons and other molecules slow the electrons down so that they don’t have as much kinetic energy available to knock off a sufficient number of other electrons with enough kinetic energy of their own to form the cascade of ions necessary for the plasma arc (avalanche breakdown). Surprisingly, higher voltages are also needed for very small gap distances (or low gas pressure) because the electrons may have too few ionizing collisions to initiate an avalanche. The following video nicely illustrates these concepts.
Paschen’s Law accounts for many factors involved in relating breakdown voltage to the gap distance $(d)$ and is therefore a relatively complicated function, "Experimental verification of modified Paschen’s law in DC glow discharge argon plasma" , AIP Advances 9, 025215 (2019) https://doi.org/10.1063/1.5086246:
\begin{equation*}
V_B = \frac{Bpd}{ln(Apd)-ln(ln(1+1/\gamma_{se}))}
\end{equation}
The complexity of Paschen’s Law suggests that we graph the function in order to better understand the information it contains. To do that, we will use standard atmospheric pressure for the gas pressure ($p$). The constants $A$ and $B$ are determined experimentally and commonly quoted values for air under standard conditions arehttps://en.wikipedia.org/wiki/Paschen%27s_law:
$A = 11.25 (\bold{Pa} \cdot \bold{m})^{-1}$ and $B = 273.75 \bold{V}/(\bold{Pa} \cdot \bold{m})$.
The secondary emission coefficient ($\gamma_{se}$) is the average number of electrons knocked off during each collision. The $\gamma_{se}$ value for air is not well established and the possible range is quite large depending on the electric field strength and gas pressure. However data suggest that for the an electric field anywhere near what we expect from our carona modeling the $\gamma_{se}$ will be around $1\times 10^{-3}$ and likely less. "DC Breakdown in Air, Oxygen, and Nitrogen at Micrometer Separations" by Matej Klas and Stefan Matejcik, Department of Experimental Physics, Comenius University. To start we will assume $\gamma_{se} =1\times 10^{-3}$ and later we will determine how the value of $\gamma_{se}$ actually affects on our final answer for the maximum voltage on the Van de Graaff.
8) Use a graphing calculator such as Desmos to plot Paschen’s law with $V_B$ on the vertical axis and gap ($d$) on the horizontal axis. Use the values listed above for A, B, and $\gamma_{se}$. Set the vertical axis to range from [0 V – 1000 V] and the horizontal axis to range from [0 m – 0.0001 m]. (When using Desmos, click the wrench in the upper right of the plot to set axes).
9) At this point in your lab submission paste an image of your graph with the axes settings above. You can use the share graph feature of Desmos to export an image of your graph or you can just paste a screenshot showing your Desmos window.
10) The plot should show you that a minimum voltage necessary for arc discharge occurs at a certain gap distance, but greater voltage is required for larger gaps and also smaller gaps. However, the maximum arc gap that we found experimentally was 0.5 m, which is many order of magnitude larger that what you currently see in the plot. To view the plots of Paschen’s Law for larger gaps like 0.5 m, set your horizontal axes to the range [0 m – 1 m] and the vertical axis the range of [0 V – 2 million V].
11) At this point in your lab submission paste an image of your graph with the axes settings above. You can use the share graph feature of Desmos to export an image of your graph or you can just paste a screenshot showing your Desmos window.
12) Use your plot to find the predicted breakdown voltage for the 0.5 m gap and record below.
13) Remember that 0.5 m was the maximum gap over which the dome would arc discharge, so the breakdown voltage corresponding to that distance should be the maximum voltage between the Van de Graff and the grounding rod. By definition the grounding rod is at zero potential so this maximum dome voltage is relative to ground (zero potential). Compare this max voltage to the max voltage predicted by the carona discharge model. Are they similar?
14) You may have noticed that the maximum voltage predicted by the two methods was somewhat different (although they were within the same order of magnitude, meaning the greater one was much less than 10x greater). Do some research on the typical voltages achieved by demonstration Van de Graaff Generators like the one in the video to conclude which result is likely to be more accurate. Explain your reasoning and cite your sources.
FURTHER QUESTIONS
There are several reasons to doubt that Paschen’s Law would give very accurate predictions for breakdown voltage in this experimental setup. First, through a brief search was not able to find data that supported Paschen’s Law for very large gap distances such as ours. Most of the data was for gaps in the micrometer range. It is possible that Paschen’s Law is not accurate for very large gap distances. Second, Panchen’s law was developed for electrodes of equal radius, but ours were not. The radius of the grounding rod blub was very much smaller than the radius of the dome. The induced charge in the smaller radius electrode may lead to a very strong electric field that provides ions with a greater acceleration, and thus reduces the required breakdown voltage. You may also be wondering about the influence of $\gamma_{se}$. We used a specific value for $\gamma_{se}$ in the arc discharge model, but we know there is a very high uncertainty associated with that value. Let’s investigate how much that could have affected our results and conclusions.
16) Add 3 more plots using values of $\gamma_{se}$ that are one order of magnitude larger and two orders of magnitude smaller than the expected upper limit of $1\times 10^{-3}$ or less ($\gamma_{se} = 0.01, 0.0001, 0.00001$). You should get something like this:
17) Even though we varied $\gamma_{se}$ by four orders of magnitude the predicted breakdown voltage for a 0.5 m gap saw a relatively small change. Calculate the % difference between the largest and smallest predicted voltages. Show your work.
18) Would you say that being uncertain of the $\gamma_{se}$ value significantly impacted the results and conclusions of this work? Explain.
19) Reset the vertical axis in your plot to range from [0 V – 1000 V] and the horizontal axis to range from [0 m – 0.001 m]. (When using Desmos, click the wrench in the upper right of the plot to set axes).
20) At this point in your lab submission paste an image of your graph with the axes settings above. You can use the share graph feature of Desmos to export an image of your graph or you can just paste a screenshot showing your Desmos window.
21) If our gap distance had actually been in this this range up to 0.0001 m (100 micrometers) would the uncertainty in $\gamma_{se}$ have significantly affected our results and conclusions? Explain.
17
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The following video demonstrates the experimental setup and the collection of all necessary data for this lab.
First we will determine if the wire in the rheostat is made of an Ohmic material (follows Ohm’s Law).
1) Write Ohm’s Law in the form where voltage is isolated on the left:
2) According to Ohm’s Law, what type of function should relate voltage and current? (proportional, linear, quadratic, etc.)?
3) Use the data provided in the video to plot the voltage on the vertical axis and current on the horizontal axis. Title your graph and label the axes, including units.
4) Fit the expected type of function to the data and record the fit function and R2 value here:
5) Does the material appear to be Ohmic? Explain how your data and fit equation lead to your conclusion.
6) Typically we plot the independent variable on the horizontal axis and dependent variable on the vertical axis. We controlled the voltage, so that was our independent variable, and we measured the resulting current, so that was our dependent variable. However, we switched our plot axes so that the slope of would correspond directly to a particular physical quantity (instead of the inverse of that quantity). What quantity does the slope of your fit function represent? Explain.
7) What is the resistance of the rheostat at the particular position used for this Ohm’s Law test. (Be sure to include units!)
We will use the common conductor resistance model that assumes the conductor is:
The result of this model is an expression for resistance that depends only on conductor length ($L$), cross sectional area ($A$), and material resistivity $\rho$.
$R = \rho\frac{L}{A}$
8) As a by product, the Ohm’s Law experiment has already provided you with one value for the resistance at a particular rheostat position. The video provides you with that position value and an additional four measurements of resistance at different positions. Create a spreadsheet to record the resistance and position data, including the value from the Ohm’s Law test.
9) As described in the video, we need to convert the measured rheostat position to an actual wire length if we want to model the resistance. As seen in the video, there are 10 turns for each centimeter of rheostat position. The circumference of the turns can be found from the measured turn diameter of 5.34 cm. Create a conversion factor between rheostat position in cm and actual wire length in meters. Show you work. [Hint: Apply unit analysis techniques!]
10) Use your conversion factor and the formula features of the spreadsheet to efficiently add a column to your spreadsheet that calculates the wire length in meters.
11) Plot the measured resistance vs. the wire length in meters (resistance on vertical axis). Title your graph and label the axes, including units.
12) Looking back at the resistance model, what type of function should fit the resistance vs. length data (proportional, linear, quadratic, etc.)? Explain.
13) Apply the type of fit predicted by the resistance model and record the fit equation and R2 values here:
14) The resistance model predicts zero resistance when the wire length is zero, but your fit function does not (it has a non-zero y-intercept). Why would there be a non-zero resistance when the rheostat wire length was zero?
15) Based on your fit function, what is the total resistance of the wires used to connect the rheostat to the multimeter? (What is the resistance when the length of rheostat wire is zero?)
16) Looking back at the resistance model equation, and recognizing that we plotted resistance on the y-axis and length on the x-axis, we can see that the slope of the fit function should represent a specific combination of wire properties. Rewrite the equation below, but replacing the question mark with the symbol for the correct wire property.
$slope = \frac{\rho}{?}$
17) Use the actual value of your slope in the previous equation to solve for the resistivity of the wire. Show your work, including units.
18) Does the data indicate that the material is Ohmic and and can also be modeled using the simple linear resistance model? Explain.
19) Look at this table of resistivity values or this one to determine the wire material. Explain your choice. (Be careful with units!)
FURTHER QUESTIONS
20) Now that you have identified the material, do some research on that material in order to learn and then explain below why it was chosen for use in the rheostat.
18
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
The following video demonstrates the experimental setup and the collection of all necessary data for this lab. You can copy the data from this online spreadsheet and paste into your own for analysis.
1) Draw a standard circuit diagram of the capacitor charge/discharge circuit that is described/shown in the video.
2) The data in the spreadsheet contains data from before the switch was thrown to begin discharging. We will need to adjust the dat in order to model the data with the expected type of function. Plot the voltage vs. time for the discharging data. Be sure to title your graph and label your axes, including units.
3) What function do you expect will fit the voltage discharge data? Write it below and explain your reasoning and/or cite your source.
4) In order to apply the expected fit function we need to adjust the time values so that discharge begins at time zero. Identify the point at which the voltage first begins to drop. Keep one voltage data point before that, and delete the previous values in the voltage column only (shift the voltage values up). This will shift the time axis so that time zero corresponds to the initial voltage just before charging begins. (The original raw data is stored in the online spreadsheet so we aren’t worried about losing data that could be important later).
5) Fit the data with the function type you chose above. Write the resulting fit function and R2 value here:
6) What is the value of the discharge time constant indicated by you fit function? [Hint: You don’t see this value explicitly in the fit function produced by your spreadsheet, but you do see it’s inverse.]
7) Repeat steps 1 and 2 for the charging data.
8) What type of function should fit the voltage vs. time while charging? Explain your reasoning and/or cite your source.
9) This type of function may not be an option to choose from in your spreadsheet. To get around that, make a new column that plots the difference between the power supply voltage and the capacitor voltage. (To find the power supply voltage you can look at the last voltage value in the charging data, which should be similar to the first value in the charging data). No change your graph options to instead plot the difference in voltage vs. time.
10) What type of function should fit the voltage difference data while charging? Show your work in demonstrating your answer mathematically.
11) Fit the correct function type to the charging data. Record the resulting fit function and R2 value here:
12) What is the value of the discharge time constant indicated by you fit function?
13) We expect the discharging and charging time constants to be the same. Does this appear to be the case? Explain your answer.
14) To calculate the capacitance of the capacitor from the time constant value we need to know the value of the resistor. Use the resistor code shown in the video to determine the resistance. Cite any sources you used.
15) Average the two time constants and use the average value to calculate the capacitance of the capacitor and provide answers in both Farads and µF (microFarads) Show your work.
16) Calculate a % difference between the value you found experimentally and the value printed on the capacitor.
17) Now we would like to determine the time constant due to leakage. Repeat steps 1-5 for the leakage data.
18) How long would it take for this capacitor to lose to 63% of it’s voltage (drop to 37% of it’s original voltage)? Explain/show your work.
19) How long would it take this capacitor to lose half of its voltage? Show your work.
20) What is the half-life for charge stored on this capacitor? Explain.
21) Based on the results of your experiments, are you confident in the capacitance value you found? Explain in terms of R2 values for your fits and relative similarity between your two values.
22) Would you consider using this capacitor in a circuit that required the capacitor to maintain at least 50% of it’s voltage for 30 seconds? Explain.
FURTHER QUESTIONS
We were unable to characterize the time constant of the small ceramic capacitor because it was too short compared to the minimum sampling period of the digital voltage probe (0.01s). However, we were able to use slow motion video to capture a faint trace of the discharge on the oscilloscope display. The image below shows just such a frame from that video.

In order to use this trace to determine the time constant we need to know the scale. The following photo shows the oscilloscope settings.

As highlighted in the photo, above the volts per division (vertical axis) is set to 0.5, so the total voltage change seen in the trace is 2 volts (four boxes). The time per division is set to 50 µs, so the time to nearly full charge is about 100 µs. To find the time constant we want to measure the time for the voltage to reach 63% of the charging voltage (2 Volts).
22) Calculate 63% of 2V.
23) Notice that there are 4 small tick marks within the large boxes, which divides them into division of 1/5 the large box value. Use a ruler to help you find where the curve reaches 63% of 2V and then read off the time from beginning of charging to that point. Record the time constant below. (The large boxes are 50 µs on the horizontal axis, so each small tick mark is 10 µs).
25) Now you know know the time constant for the small capacitor to discharge through the resistor (which hasn’t changed). Calculate the capacitance value and provide answers in both Farads and nF (nanoFarads). Show your work. .
As discussed in the video, we were unable to trust the measured leakage discharge curve for the small capacitor because we could not verify the apparent leakage discharge was not actually discharge through circuitry of the the voltage probe. (This is a common difficulty in measuring leakage time constants for small capacitors). However, the voltage probe is designed to have a 10MΩ input impedance (we’ll learn more about impedance when we discuss AC circuits, but for this DC circuit that means a 10MΩ input resistance). Now that we know the capacitance and we know the resistance in the voltage probe circuit we can calculate the expected time constant for discharge through the voltage probe.
26) Calculate the expected time constant for discharge through the voltage probe. Show your work.
28) The measured leakage discharge data for the small capacitor has already been processed for you. Plot the voltage vs. time data, fit the expected function type, and determine the time constant for this discharge. Write your fit function, R2 value, and time constant below.
29) If the measured leakage discharge time constantis much smaller (about 10x) than the expected time constant for discharge through the voltage probe then we might assume that probe circuitry discharge is not contributing significantly to the measured discharge, in which case we might trust the measured time constant to be the true leakage time constant. However, if that is not the case and the expected time constant for probe circuitry discharge is actually comparable to the measured leakage time constant then we know probe discharge is likely contributing significantly to the overall discharge. In that case, we can’t trust the time constant we found above to be the true leakage time constant. Which is the case in this experiment? Explain your answer.