1.4 Solving Linear Equations

Introduction

You are shopping at Old Navy for seven new outfits. The price points are [latex]\$10[/latex] and [latex]\$30[/latex]. You really like the [latex]\$30[/latex] outfits; however, your total budget can’t exceed [latex]\$110[/latex]. How do you spend [latex]\$110[/latex] to acquire all the needed outfits without exceeding your budget while getting as many [latex]\$30[/latex] items as possible?

This is a problem of linear equations, and it illustrates how you can use them to make an optimal decision. Let [latex]L[/latex] represent the quantity of clothing at the low price point of [latex]\$10[/latex], and [latex]H[/latex] represent the quantity of clothing at the high price point of [latex]\$30[/latex]. This results in the following algebraic equations:

[latex]\begin{eqnarray*}L\;+\;H\;&=&\;7\;\text{(the total number of outfits you need)}\\\$10L+\$30H\;&=&\;\$110\;\text{(your total budget)}\end{eqnarray*}[/latex]

By simultaneously solving these equations you can determine how many outfits at each price point you can purchase.

You will encounter many situations like this in your business career, for example, in making the best use of a manufacturer’s production capacity. Assume your company makes two products on the same production line and sells all its output. Each product contributes differently to your profitability, and each product takes a different amount of time to manufacture. What combination of each of these products should you make such that you operate your production line at capacity while also maximizing the profits earned? This section explores how to solve linear equations for unknown variables.

Understanding Equations

To manipulate algebraic equations and solve for unknown variables, you must first become familiar with some important language, including linear versus nonlinear equations and sides of the equation.

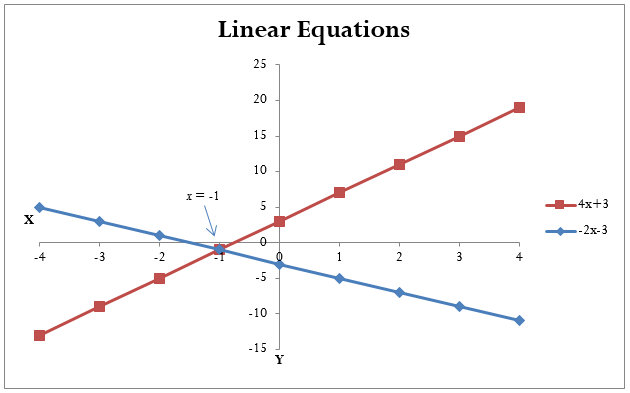
[latex]\Large 4x+3=-2x-3[/latex]

[latex]4x+3[/latex] is the Left side: Every equation has two sides. Everything to the left side of the equal sign is known as the left side of the equation.
[latex]-2x-3[/latex] is the Right side: Everything to the right side of the equal sign is known as the right side of the equation.
[latex]x[/latex] is the Variable x: Observe two important features of this variable:

1. 1. Note that the variable has an exponent of [latex]1[/latex]. So if you were to plot each algebraic expression onto a Cartesian coordinate system, the expressions would form straight lines (see Figure 1.4.1a). Such equations are called linear equations. Because each equation has only one variable, there is only one solution that makes the equation true. In business mathematics, this is the most common situation you will encounter.
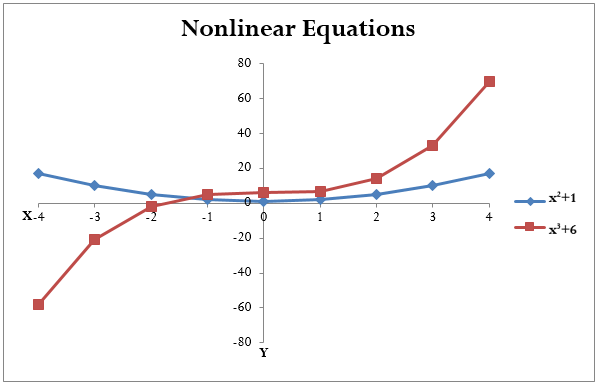
   2. If the exponent is anything but a one, the equation is a nonlinear equation since the graph of the expression does not form a straight line. Figure 1.4.1b illustrates two algebraic expressions where the exponent is other than a [latex]1[/latex].

The goal in manipulating and solving a linear equation is to find a value for the unknown variable that makes the equation true. If you substitute a value of [latex]x =−1[/latex] into the above example, the left-hand side of the equation equals the right-hand side of the equation (see Figure 1.4.1a). The value of [latex]x =−1[/latex] is known as the root, or solution, to the linear equation.

Solving One Linear Equation with One Unknown Variable

In your study of solving linear equations, you need to start by manipulating a single equation to solve for a single unknown variable. Later in this section you will extend from this foundation to the solution of two linear equations with two unknowns.

HOW TO Determine the root of a linear equation with only one unknown variable

Apply the following steps:

Step 1: Your first goal is to separate the terms containing the literal coefficientliteral coefficient from the terms that only have numerical coefficients. Collect all of the terms with literal coefficients on only one side of the equation and collect all of the terms with only numerical coefficients on the other side of the equation. It does not matter which terms go on which side of the equation, so long as you separate them.

Step 2: To move a term from one side of an equation to another, take the mathematical opposite of the term being moved and add it to both sides.

For example, if you want to move the [latex]+3[/latex] in [latex]4x+3=−2x−3[/latex] from the left-hand side to the right-hand side, the mathematical opposite of [latex]+3[/latex] is [latex]−3[/latex]. When you move a term, remember the cardinal rule: What you do to one side of an equation you must also do to the other side of the equation. Breaking this rule breaks the equality in the equation.

Step 3: Combine all like terms on each side and simplify the equation according to the rules of algebra.

Step 4: In the term containing the literal coefficient, reduce the numerical coefficient to a [latex]1[/latex] by dividing both sides of the equation by the numerical coefficient.

Things To Watch Out For

When you move a term from one side of the equation to another using multiplication or division, remember that this affects each and every term on both sides of the equation. To remove the [latex]x[/latex] from the denominator in the following equation, multiply both sides of the equation by [latex]x[/latex]:

[latex]\begin{align*}\frac5x+\frac1x=\frac2x+2\end{align*}[/latex]

becomes:

[latex]\begin{align*}x\left(\frac5x+\frac1x\right)=\left(\frac2x+2\right)x\end{align*}[/latex]

which then becomes:

[latex]5+1=2+2x[/latex]

Multiplying every term on both sides by [latex]x[/latex] maintains the equality.

 Paths To Success

Negative numbers can cause some people a lot of grief. In moving terms from a particular side of the equation, many people prefer to avoid negative numerical coefficients in front of literal coefficients. Revisiting [latex]4x+3=-2x−3[/latex], you could move the [latex]4x[/latex] from the left side to the right side by subtracting [latex]4x[/latex] from both sides. However, on the right side this results in [latex]−6x[/latex]. The negative is easily overlooked or accidentally dropped in future steps. Instead, move the variable to the left side of the equation, yielding a positive coefficient of [latex]6x[/latex].

Example 1.4.2

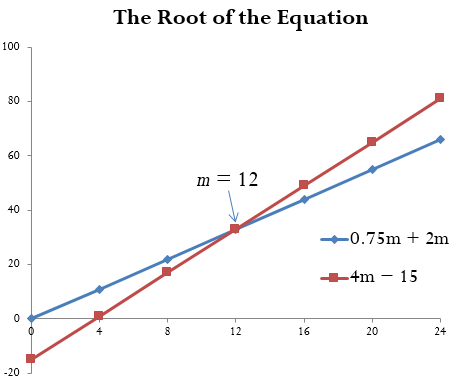
Solve the following equation for [latex]m[/latex]:

[latex]\begin{align*}\frac{3m}4+2m=4m-15\end{align*}[/latex].

Solution

Step 1: Simplify all fractions to make the equation easier to work with.

Still simplifying, collect like terms where possible.

[latex]0.75m +2=4m-15[/latex].

Step 2: Collect all terms with the literal coefficient on one side of the equation. Move all terms with literal coefficients to the right-hand side.

[latex]2.75m = 4m-15[/latex].

Step 3: Combine like terms and move all terms with only numerical coefficients to the left-hand side.

[latex]2.75m - 2.75m = 4m - 15 - 2.75m[/latex].

On the left-hand side, the [latex]+2.75m[/latex] and [latex]−2.75m[/latex] cancel each other out. Now move the numerical coefficients to the left-hand side.

[latex]0 = 4m - 15 -2.75m[/latex]

On the right-hand side, the [latex]−15[/latex] and [latex]+15[/latex] cancel each other out.

[latex]0 + 5 = 4m - 15  - 2.75m + 15[/latex]

Step 4: Combine like terms on each side.

[latex]0 + 5 = 4m - 2.75m[/latex]

Step 5: Divide both sides by the numerical coefficient that accompanies the literal coefficient.

Simplify.

[latex]15 = 1.25m[/latex]

[latex]\frac{15}{1.25} = \frac{1.25m}{1.25}[/latex]

[latex]12 = m[/latex]

Step 6: Write a statement.

The root of the equation is [latex]m=12[/latex].

This makes both sides of the equation ([latex]\frac{3m}4+2m[/latex] and [latex]4m-15[/latex]) equal [latex]33[/latex].

 

Solving Two Linear Equations with Two Unknown Variables

The manipulation process you have just practiced works well for solving one linear equation with one variable. But what happens if you need to solve two linear equations with two variables simultaneously? Remember when you were at Old Navy purchasing seven outfits earlier in this chapter? You needed to stay within a pricing budget. Each equation had two unknown variables representing the number of lower-priced outfits ([latex]L[/latex]) and higher-priced outfits ([latex]H[/latex]).

[latex]\begin{eqnarray*}L\;+\;H\;&=&\;7\;\text{(the total number of outfits you need)}\\\$10L+\$30H\;&=&\;\$110\;\text{(your total budget)}\end{eqnarray*}[/latex]

The goal is to reduce two equations with two unknowns into a single linear equation with one unknown. Once this transformation is complete, you then identify the unknown variable by applying the three-step procedure for solving one linear equation, as just discussed.

When you work with two linear equations with two unknowns, the rules of algebra permit the following two manipulations:

• What you do to one side of the equation must be done to the other side of the equation to maintain the equality. Therefore, you can multiply or divide any equation by any number without changing the root of the equation.
  • For example, if you multiply all terms of [latex]x + y = 2[/latex] by [latex]2[/latex] on both sides, resulting in [latex]2x + 2y = 4[/latex], the equality of the equation remains unchanged and the same roots exist.
• Terms that are on the same side of an equation can be added and subtracted between equations by combining like terms. Each of the two equations has a left side and right side. This rule permits taking the left side of the first equation and either adding or subtracting like terms on the left side of the second equation. When you perform this action, remember the first rule above. If you add the left sides of the equations together, you then must add the right side of both equations together to maintain equality.

HOW TO  Solve two linear equations with two unknown variables

• Step 1: Write the two equations one above the other, vertically lining up terms that have the same literal coefficients and terms that have only the numerical coefficient. If necessary, the equations may need to be manipulated such that all of the literal coefficients are on one side with the numerical coefficients on the other side.
• Step 2: Examine your two equations. Through multiplication or division, make the numerical coefficient on one of the terms containing a literal coefficient exactly equal to its counterpart in the other equation.
• Step 3: Add or subtract the two equations as needed so as to eliminate the identical term from both equations.
• Step 4: In the new equation, solve for the last literal coefficient.
• Step 5: Substitute the root of the known literal coefficient into either of the two original equations. If one of the equations takes on a simpler structure, pick that equation.
• Step 6: Solve your chosen equation for the other literal coefficient.

 Paths To Success

Sometimes it is unclear exactly how you need to multiply or divide the equations to make two of the terms identical. For example, assume the following two equations:

[latex]4.9x + 1.5y = 38.3[/latex]

[latex]2.7x − 8.6y = 17.8[/latex]

If the goal is to make the terms containing the literal coefficient [latex]x[/latex] identical, there are two alternative solutions:

• Take the larger numerical coefficient for [latex]x[/latex] and divide it by the smaller numerical coefficient. The resulting number is the factor for multiplying the equation containing the smaller numerical coefficient. In this case, [latex]4.9\;\div\;2.7\;=\;1.\overline{814}[/latex]. Multiply all terms in the second equation by [latex]1.\overline{814}[/latex] to make the numerical coefficients for [latex]x[/latex] equal to each other, resulting in this pair of equations: 

[latex]\begin{eqnarray*}4.9x+1.5y&=&38.3\\&\text{and}\;\\4.9x-15.6\overline{074}y&=&32.3\overline{037}\;\text{(every term multiplied by 1.}\overline{\text{814}}\text{)}\end{eqnarray*}[/latex]

• Take the first equation and multiply it by the numerical coefficient in the second equation. Then take the second equation and multiply it by the numerical coefficient in the first equation. In this case, multiply all terms in the first equation by [latex]2.7[/latex]. Then multiply all terms in the second equation by [latex]4.9[/latex].

[latex]13.23x+4.05y=103.41 \text{(every term multiplied by 2.7)}[/latex]

[latex]13.23x-\;42.14y=87.22 \text{(every term multiplied by 4.9)}[/latex]

Note that both approaches successfully result in both equations having the same numerical coefficient in front of the literal coefficient [latex]x[/latex].

Paths To Success

Ultimately, every pairing of linear equations with two unknowns can be converted into a single equation through substitution. To make the conversion, do the following:

1. 1. Solve either equation for one of the unknown variables.
   2. Take the resulting algebraic expression and substitute it into the other equation. This new equation is solvable for one of the unknown variables.
   3. Substitute your newfound variable into one of the original equations to determine the value for the other unknown variable.

Take the following two equations:

[latex]a+b=4 \text{and } 2a+b=6[/latex]

1. 1. Solving the first equation for [latex]a[/latex] results in [latex]a = 4-b[/latex].
   2. Substituting the expression for [latex]a[/latex] into the second equation and solving for [latex]b[/latex] results in [latex]2(4-b) b=6[/latex], which solves as [latex]b=2[/latex].
   3. Finally, substituting the root of [latex]b[/latex] into the first equation to calculate [latex]a[/latex] gives [latex]a + 2 = 4[/latex] resulting in [latex]a = 2[/latex]. Therefore, the roots of these two equations are [latex]a = 2[/latex] and [latex]b = 2[/latex].

Paths To Success

One of the most difficult areas of mathematics involves translating words into mathematical symbols and operations. To assist in this translation, the table below lists some common language and the mathematical symbol that is typically associated with the word or phrase.

Table 1.4.1

Language				Math Symbol		Language				Math Symbol
Sum Addition	In addition to In excess		Increased by Plus	+		Subtract Decreased by Diminished by	Less Minus	Difference Reduced by		−
Divide Division	Divisible Quotient		Per	÷		Multiplied by Times	Percentage of		Product of Of	×
Becomes Is/Was/Were		Will be	Results in Totals	=		More than Greater than				>
Less than		Lower than		<		Greater than or equal to				≥
Less than or equal to				≤		Not equal to				≠

Example 1.4.5

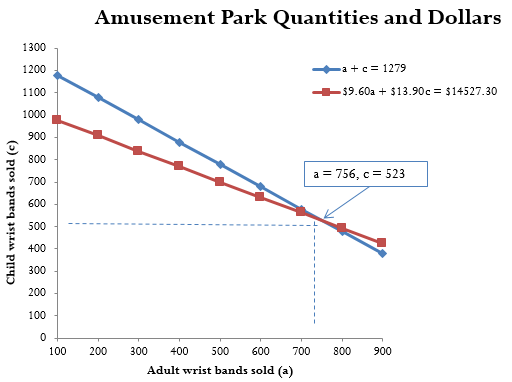
Tinkertown Family Fun Park charges [latex]\$15[/latex] for a child wrist band and [latex]\$10.50[/latex] for an adult wrist band. On a warm summer day, the amusement park had total wrist band revenue of [latex]\$15,783[/latex] from sales of [latex]1,279[/latex] wrist bands. How many adult and child wrist bands did the park sell that day?

Solution

Step 1: Write out what you know. 

• The price of the wrist bands, total quantity, and sales are known.
• Child wrist band price = $15
• Adult wrist band price = $10.50
• Total revenue = $15,783
• Total unit sales = 1,279
• The quantity of adult wrist bands sold and the quantity of child wrist bands sold are unknown:
• Adult wrist bands quantity [latex]= a[/latex]
• Child wrist bands quantity [latex]= c[/latex]

Step 2: Write out how you will get to the solution. 

1. Work with the quantities first. Calculate the total unit sales by adding the number of adult wrist bands to the number of child wrist bands: # of adult wrist bands + # of child wrist bands = total unit sales
   a + c = 1,279
2. Now consider the dollar figures. Total revenue for any company is calculated as unit price multiplied by units sold. Inthis case, you must sum the revenue from two products to get the total revenue.

Total adult revenue + Total child revenue = Total revenue
(Adult price×Adult quantity)+(Child price×Child quantity)=Total revenue $10.50a + $15c = $15,783

3. Apply the six-step procedure for solving two linear equations with two unknowns

Step 3: Write the equations one above the other and line them up.

[latex]a+c=1,279[/latex]

[latex]$10.50a+$15c=$15,783[/latex]

Step 4: Multiply all terms in the first equation by [latex]10.5[/latex], resulting in a having the same numerical coefficient in both equations.

[latex]10.50a + 10.50c = 13,429.50[/latex]

[latex]$10.50a + $15c = $15,783[/latex]

Step 5: Subtract the equations by subtracting all terms on both sides.

[latex]10.5a + 10.5c = 13,429.50[/latex]

[latex]$10.50a + $15c = $15,783 Subtract[/latex]

[latex]-4.5c = -2,353.50[/latex]

Step 6: Solve for [latex]c[/latex] by dividing both sides by [latex]−4.5[/latex].

[latex]\Large \frac{-4.5c}{-4.5}=\frac{-2,353.50}{-4.5}[/latex]

[latex]c=523[/latex]

Step 7: Substitute the known value for [latex]c[/latex] into one of the original equations. The first equation is simple, so choose that one.

Solve for a by subtracting [latex]523[/latex] from both sides. You now have the roots for [latex]a[/latex] and [latex]c[/latex].

[latex]\begin{eqnarray*}a+c&=&1,279\\a+{\color[rgb]{1.0, 0.0, 1.0}523}&=&1,279\\a+{\color[rgb]{1.0, 0.0, 1.0}\cancel{523-523}}&=&1,279-{\color[rgb]{1.0, 0.0, 1.0}523}\\a&=&756\end{eqnarray*}[/latex]

Step 8: Write as a statement. 

Tinkertown Family Fun Park sold [latex]523[/latex] child wrist bands and [latex]756[/latex] adult wrist bands.

1.4.6 Exercises 

Attribution

Unit 2.6 in Introduction to Business Math by Margaret Dancy CC BY-NC-SA. which was adapted from 2.5 Linear Equations: Manipulating and Solving in Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a CC BY-NC-SA 4.0  unless otherwise noted.