5.2 Determining the Future (Maturity) Value

The simplest future value scenario for compound interest is for all of the variables to remain unchanged throughout the entire transaction. To understand the derivation of the formula, continue with the following scenario. If $4000 was borrowed two years ago at 12% compounded semi-annually, then a borrower will owe two years of compound interest in addition to the original principal of $4,000.

That means PV = $4,000. The compounding frequency is semi-annually, or twice per year, which makes the periodic interest rate [latex]i=\frac{I/Y}{C/Y}=\frac{12\%}{2}=6\%[/latex] . Therefore, after the first six months, the borrower has 6% interest converted to principal. This a future value, or FV, calculated as follows:

Principal after one compounding period (six months) = Principal plus interest

[latex]\begin{align} FV &=PV+{i}(PV)\\ &=\$ 4,000+0.06(\$ 4,000)\\ &=\$ 4,000+\$ 240=\$ 4,240 \end{align} \nonumber[/latex]

Now proceed to the next six months. The future value after two compounding periods (one year) is calculated in the same way. Note that the equation [latex]FV = PV +i(PV)[/latex] can be factored and rewritten as [latex]FV = PV(1 +i)[/latex].

[latex]FV (after\;two\;compounding\;periods)[/latex]
[latex]= PV(1 +i) =$4,200(1 + 0.06) = $4,240(1.06) = $4,494.40[/latex]

Since the [latex]PV = $4,240[/latex] is the result of the previous calculation where [latex]PV(1 + i) = $4,240[/latex], the following algebraic substitution is possible:

[latex]FV (after\;two\;compounding\;periods)[/latex]
[latex]= PV(1 +i )(1 + i) = $4,000(1.06)(1.06) = $4200(1.06) = $4,494.40[/latex]

Simplifying algebraically, you get:

[latex]FV = PV(1 +i)(1 + i) = PV(1 +i)^2[/latex]

Do you notice a pattern? With one compounding period, the formula has only one [latex](1 + i)[/latex]. With two compounding periods involved, it has two factors of [latex](1 + i)[/latex]. Each successive compounding period multiplies a further [latex](1 + i)[/latex] onto the equation. This makes the exponent on the [latex](1 + i)[/latex]  exactly equal to the number of times that interest is converted to principal during the transaction.

The Formula

First, you need to know how many times interest is converted to principal throughout the transaction. You can then calculate the future value. Use Formula 5.2A below to determine the number of compound periods involved in the transaction.

Formula 5.2A: Number of Compound Periods

[latex]n = \frac{C}{Y} \times (Number\;of \;Years)[/latex] where, [latex]\frac {C}{Y}[/latex]is the number of compounding periods per year.

Once you know n, substitute it into Formula 5.2B, which finds the amount of principal and interest together at the end of the transaction, or the future (maturity) value, FV.

Formula 5.2B: Future (Maturity)

[latex]Value: FV = PV \times (1+i)^n[/latex]

• where, PV is the resent value or principal. This is the starting amount upon which compound interest is calculated.
• i is the periodic interest rate from Formula 5.1.
• n is the number of compound periods from Formula 5.2A.

Important Notes

Calculating the Interest Amount (I):

In any situation of lump-sum compound interest, you can isolate the interest amount using the formula

[latex]I=FV−PV[/latex].

How It Works

Follow these steps to calculate the future value of a single payment:

Step 1: Calculate the periodic interest rate (i) using the formula

[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}[/latex]

Step 2: Calculate the total number of compound periods (n) using the formula

[latex]n=C/Y \times \text{(Number of years)}[/latex]

Step 3: Calculate the future value using the formula

[latex]FV=PV(1+i)^n[/latex]

You will first need to calculate i and n using steps 1 and 2.

Cash Flow Sign Convention

Calculating FV (PV is given)

For investments: When money is invested (paid-out), this amount is considered as a cash-outflow and this amount has to be entered as a negative number for PV.

For Loans: When money is received (loaned), this amount is considered as a cash-inflow and this amount has to be entered as a positive number for PV.

Calculating PV (FV is given) 

For investments: When you receive your matured investment at the end of the term this is considered as a cash-inflow for you and the future value should be entered as a positive amount.

For Loans: When the loan is repaid at the end of the term this is considered as a cash-outflow for you and the future value should be entered as a negative amount.

Example 5.2.1: Making an Investment

If you invested $5,000 for 10 years at 9% compounded quarterly, how much money would you have? What is the interest earned during the term?

Solution

The timeline for the investment is below.

Step 1: Given information:

PV = 5,000; I/Y = 9%; C/Y = 4

Step 2: Calculate the periodic interest rate, i.

[latex]i=\frac{I/Y}{C/Y}=\frac{9\%}{4}=2.25\%=0.0225[/latex]

Step 3: Calculate the total number of compoundings, n.

[latex]n=C/Y \times (\text{Number of Years})=4 \times 10=40[/latex]

Step 4: Solve for the future value, FV.

[latex]FV=\$5,\!000(1+0.0225)^{40}=\$12,\!175.94[/latex]

Step 5: Find the interest earned.

[latex]I=FV-PV= \$12,\!175.94-\$5,\!000=\$7,\!175.94[/latex]

After 10 years, the principal grows to $12,175.94, which includes your $5,000 principal and $7,175.94 of compound interest.

Future Value Calculations with Variable Changes

What happens if a variable such as the nominal interest rate, compounding frequency, or even the principal changes somewhere in the middle of the transaction? When any variable changes, you must break the timeline into separate time fragments at the point of the change. To arrive at the solution, you need to work from left to right one time segment at a time using the future value formula.

How It Works

Follow these steps when variables change in calculations of future value based on lump-sum compound interest:

Step 1: Read and understand the problem. Identify the present value. Draw a timeline broken into separate time segments at the point of any change. For each time segment, identify any principal changes, the nominal interest rate, the compounding frequency, and the length of the time segment in years.

Step 2: For each time segment, calculate the periodic interest rate (i) using Formula 5.1.

Step 3: For each time segment, calculate the total number of compound periods (n) using Formula 5.2A.

Step 4: Starting with the present value in the first time segment (starting on the left), solve for the future value using Formula 5.2B.

Step 5: Let the future value calculated in the previous step become the present value for the next step. If the principal changes, adjust the new present value accordingly.

Step 6: Using Formula 5.2B calculate the future value of the next time segment.

Step 7: Repeat steps 5 and 6 until you obtain the final future value from the final time segment.

Concept Check

Example 5.2.2: Delaying a Facility Upgrade

Five years ago Coast Appliances was supposed to upgrade one of its facilities at a quoted cost of $48,000. The upgrade was not completed, so Coast Appliances delayed the purchase until now. The construction company that provided the quote indicates that prices rose 6% compounded quarterly for the first 1½ years, 7% compounded semi-annually for the following 2½ years, and 7.5% compounded monthly for the final year. If Coast Appliances wants to perform the upgrade today, what amount of money does it need?

Solution

The timeline below shows the original quote from five years ago until today.

 

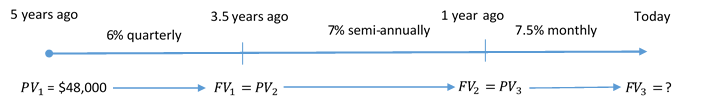
Step 1: First time segment:

PV₁ = $48,000; I/Y = 6%; C/Y = 4; Years = 2[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{4}=1.5\%[/latex][latex]n =C/Y \times (\text{Number of Years})=4 \times 1.5=6[/latex]Find FV₁[latex]\begin{align} FV_1 &= PV_1(1 + i)^n\\ &= \$48,\!000 (1 + 0.015)^6\\ &= \$24,\!500(1.015)^6\\ &= \$52,\!485.27667 \end{align}[/latex]This becomes PV₂ for the next calculation in Step 2.Step 2: Second line segment:PV₂ = FV₁ = $52,485.27667; I/Y = 7%; C/Y = 2; Years = 2.5[latex]i=\frac{I/Y}{C/Y}=\frac{7\%}{2}=3.5\%[/latex][latex]n =C/Y \times (\text{Number of Years})= 2 \times 2.5=5[/latex]Find FV₂[latex]\begin{align} FV_2 &= PV_2(1 + i)^n\\ &= \$52,\!485.27667 (1+0.035)^5\\ &= \$62,\!336.04435 \end{align}[/latex]This becomes PV₃ for the next calculation in Step 3.Step 3: Third line segment:PV₃ = FV₂ = $62,336.04435; I/Y = 7.5%; C/Y = 12; Years = 1[latex]i=\frac{I/Y}{C/Y}=\frac{7.5\%}{12}=0.625\%[/latex][latex]n =C/Y \times (\text{Number of Years})= 12 \times 1=12[/latex]Find FV₃[latex]\begin{align} FV_3 &= PV_3(1 + i)^n\\ &= \$62,\!336.04435 (1+0.00325)^{12}\\ &= \$67,\!175.35 \end{align}[/latex]

The future value is $67,175.35.

Coast Appliances requires $67,175.35 to perform the upgrade today. This consists of $48,000 from the original quote plus $19,175.35 in price increases.

Example 5.2.3: Making an Additional Contribution

Two years ago Lorelei placed $2,000 into an investment earning 6% compounded monthly. Today she makes a deposit to the investment in the amount of $1,500. What is the maturity value of her investment three years from now?

Solution

The timeline for the investment is below.

Step 1: First time segment:

PV₁ = $2,000; I/Y = 6%; C/Y = 12; Years = 2[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{12}=0.5\%[/latex][latex]n =C/Y \times (\text{Number of Years})=12 \times 2=24[/latex]Find FV₁[latex]\begin{align} FV_1 &= PV_1(1 + i)^n\\ &= \$2,\!000 (1 + 0.005)^24\\ &= \$2,\!000(1.005)^24\\ &= \$2,\!254.319552 \end{align}[/latex]$2,254.319552 + $1,500 = $3,754.319552This becomes PV₂ for the second line segment in Step 2.Step 2: Second line segment:PV₂ = FV₁ = 3,754.319552; I/Y = 6%; C/Y = 12; Years = 3[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{12}=0.5\%[/latex][latex]n =C/Y \times \text{(Number of Years)}= 12 \times 3=36[/latex]Find FV₂[latex]\begin{align} FV_2 &= PV_2(1 + i)^n\\ &= \$3,\!754.319552 (1+0.005)^{36}\\ &= \$4,\!492.72 \end{align}[/latex]The future value is $4,492.72Three years from now Lorelei will have $4,492.72. This represents $3,500 of principal and $992.72 of compound interest.

Chapter Attribution

9.2 in Business Math: A Step-by-Step Handbook by J. Olivier published by Libretexts shared under CC BY-NC-SA license.