7.3 Present Value of Annuities
The present value of any annuity is equal to the sum of all of the present values of all of the annuity payments when they are moved to the beginning of the first payment interval. For example, assume you will receive $1,000 annual payments at the end of every payment interval for the next three years from an investment earning 10% compounded annually. How much money needs to be in the annuity at the start to make this happen? In this case, you have an ordinary simple annuity.
With an annuity due, the first payment occurs at the beginning of the first period. The key difference is that the annuity due has one less compound of interest to remove.
The Formula
Formula 7.3A: Ordinary Annuity Present Value:
[latex]PV_{ORD} = PMT [\frac {1-(1+i)^-n}{i}][/latex]
Formula 7.3B: Annuity Due Present Value
[latex]PV_{DUE} = PMT [\frac {1-(1+i)^-n}{i}] \times (1+i)[/latex]
where,
- PMT is the regular payment amount.
- i is the periodic interest rate.
- n is the total number of payments.
How to Use the Present Value Formula for Ordinary Annuities and Annuities Due
For simple annuities you need to calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}[/latex]
For general annuities you need to calculate the equivalent periodic rate (ieq) that matches the payment interval using the formula
[latex]i{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1[/latex]
where,
- i is the given periodic rate.
- C/Y is the number of compounds per year.
- P/Y is the number of payments per year.
The present value formula for general annuities then becomes
[latex]PV_{ORD}=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right][/latex]
[latex]PV_{DUE}=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right] \times(1+i_{eq})[/latex]
How It Works
There is a five-step process for calculating the present value of any ordinary annuity or annuity due.
Step 1: Identify the annuity type. Draw a timeline to visualize the question.
Step 2: Identify the known variables, including FV, I/Y, C/Y, PMT, P/Y, and Years.
Step 3: Calculate the periodic interest rate (i). See Important Notes above.
Calculate the number of payments (n) using the formula
[latex]n= P/Y \times \text{(Number of Years)}[/latex]
Step 4: If FV = $0, proceed to step 5. If there is a nonzero value for FV, treat it like a single payment and calculate the present value PV1 using Formula 5.3A.
[latex]\begin{align}PV_1&=\frac{FV}{(1+i)^n}\end{align}[/latex]
Step 5: Apply Formulas 7.3A or 7.3B to calculate the present value of the payments.
If you calculated a present value in step 4, combine the present values from steps 4 and 5 to arrive at the total present value.
Calculating the Interest Amount
If you are interested in knowing how much interest was removed in the calculation of the present value you can use the formula
[latex]I=(n \times PMT+FV)-PV[/latex]
where,
- n is the number of payments made.
- PMT is the amount of payment.
- FV is the balance still owing.
- PV is the principal amount or present value.
Concept Check
Example 7.3.1: Amount Needed at Time of Retirement
Rodriguez is planning on having an annual gross income of $50,000 at the end of every year when he retires at age 65. He is planning for the account to be emptied by age 78, which is the average life expectancy for a Canadian man. If the account earns 5.1% compounded annually, what amount of funds needs to be in the account when he retires?
Solution
Step 1: The payments are at the end of the payment intervals, and the compounding period and payment intervals are the same. This is, therefore, an ordinary simple annuity. Calculate its value at the start, which is its present value, or PVORD.
The timeline for the client’s account appears below.

Step 2: Given information:
FV = $0; I/Y = 5.1%; C/Y = 1; PMT = $50,000; P/Y = 1; Years = 13
Step 3: Calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{5.1\%}{1}=5.1\%[/latex]
Step 4: Since FV=$0, skip this step.
Step 5: Apply Formula 9.3A to calculate the present value of the payments, PVORD.
[latex]n= P/Y \times \text{(Number of Years)}=1 \times 13=13[/latex]
[latex]\begin{align} PV_{ORD}&=PMT \left[\frac{1-(1+i)^{-n}}{i}\right]\\ &=\$50,\!000\left[\frac{1-(1+0.051)^{-13}}{0.051}\right]\\ &=\$50,\!000\left[\frac{0.476201}{0.051}\right]\\ &=\$466,\!863.69 \end{align}[/latex]
Therefore, PVORD = PV = $466,863.69
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 13 | 5.1 | Answer: -466,863.694 | 50,000 | 0 | 1 | 1 |
The figure shows how much principal and interest make up the payments. Rodriguez will need to have $466,863.69 in his account when he turns 65 if he wants to receive 13 years of $50,000 payments.
Example 7.3.2: Leaving an Inheritance
Recalculate Example 7.3.1 applying three changes:
- Rodriguez wants to leave a $100,000 inheritance for his children (assuming he dies at age 78).
- Payments are at the beginning of the year.
- His interest rate is 5.1% compounded semi-annually.
Calculate the present.
Solution
Step 1: The payments are made at the beginning of the payment intervals, and the compounding period (semiannually) and payment intervals (annually) are different. This is now a general annuity due. Calculate its value at the start, which is its present value, or PVDUE.
The timeline for the client’s account appears below.

Step 2: Given information:
FV = $100,000; I/Y = 5.1%; C/Y = 2; PMT = $50,000; P/Y=1; Years = 1
Step 3: Since P/Y [latex]\ne[/latex] C/Y, calculate the equivalent periodic rate (ieq) that matches the payment interval.
[latex]i=\frac{I/Y}{C/Y}=\frac{5.1\%}{2}=2.55\%[/latex]
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.0255)^{\frac{2}{1}}-1=0.05165025\;\text{per year}[/latex]
Step 4: Apply Formula 5.3A to calculate the present value, PV1.
FV = $100,000;
[latex]n=P/Y \times \text{(Number of Years)}=1 \times 13=13[/latex]
[latex]\begin{align} PV_1&=\frac{FV}{(1+i_{eq})^n}\\ &=\frac{\$100,\!000}{(1+0.05165025)^{13}}\\ &=\$51,\!960.42776 \end{align}[/latex]
Step 5: Apply Formula 7.3A to calculate the present value of the payments, PVDUE.
[latex]\begin{align} PV_{DUE}&=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right] \times(1+i_{eq})\\ &=\$50,\!000 \left[\frac{1-(1+0.05165025)^{-13}}{0.05165025}\right] \times(1+0.05165025)\\ &=\$489,\!066.6372 \end{align}[/latex]
Combine steps 4 and 5 to calculate the total present value, PV.
PV = $51,960.42776 + $489,066.6372 = $541,027.07
Step 6: Calculate the amount of interest.
[latex]\begin{align} I&=(n \times PMT+FV)-PV\\ &=(13 \times \$50,\!000+\$100,\!000)-\$541,\!027.07\\ &=\$750,\!000-\$541,\!027.07\\ &=\$208,\!972.93 \end{align}[/latex]
Calculator instructions:
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 13 | 5.1 | Answer: -541,027.065 | 50,000 | 100,000 | 1 | 2 |
The figure shows how much principal and interest make up the payments. Rodriguez will require more money, needing to have $541,027.07 in his account when he turns 65 if he wants to receive 13 years of $50,000 payments while leaving a $100,000 inheritance for his children. His account will earn $208,972.93 over the time frame.
Example 7.3.3: Adjusting for Inflation
Continuing with the previous two examples, Rodriguez realizes that during his retirement he needs to make some type of adjustment to his annual gross income to account for the rising cost of living. Consequently, he will take $50,000 at the beginning of each year for six years, then increase it to $60,000 for the balance. Assume his interest rate is still 5.1% semiannually and that he still wants to leave a $100,000 inheritance for his children. How much money needs to be in his retirement fund at age 65?
Solution
Step 1: There is a change of variables after six years. As a result, you need two time segments. In both segments, payments are made at the beginning of the period, and the compounding periods and payment intervals are different. These are two consecutive general annuities due. You need to calculate the resulting present value, or PVDUE.
The timeline for the client’s account appears below.
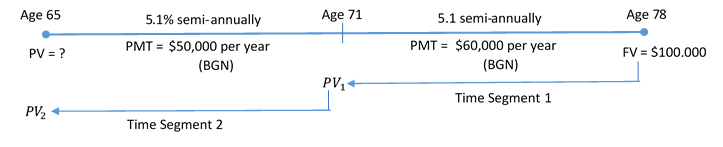
Step 2: Given information:
Time Segment 1: FV = $100,000; I/Y = 5.1%; C/Y = 2; PMT = $60,000; P/Y = 1; Years = 7
Time Segment 2: FV = PV1; I/Y = 5.1%; C/Y = 2; PMT = $50,000; P/Y = 1; Years = 6
For the first time segment:
Step 3: Since P/Y [latex]\ne[/latex] C/Y, calculate the equivalent periodic rate (ieq) that matches the payment interval.
[latex]i=\frac{I/Y}{C/Y}=\frac{5.1\%}{2}=2.55\%[/latex]
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.0255)^{\frac{2}{1}}-1=0.05165025\;\text{per year}[/latex]
Step 4: Apply Formula 9.3A to calculate the present value, PV(1).
FV=$100,000;
[latex]n=P/Y \times \text{(Number of Years)}=1 \times 7=7[/latex]
[latex]\begin{align} PV_{(1)}&=\frac{FV}{(1+i_{eq})^n}\\ &=\frac{\$100,\!000}{(1+0.05165025)^{7}}\\ &=\$70,\!291.15736 \end{align}[/latex]
Step 5: Apply Formula 7.3B to calculate the present value of the payments.
[latex]\begin{align} PV_{DUE_1}&=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right] \times(1+i_{eq})\\ &=\$60,\!000 \left[\frac{1-(1+0.05165025)^{-7}}{0.05165025}\right] \times(1+0.05165025)\\ &=\$362,\!940.8778 \end{align}[/latex]
Combine steps 4 and 5 to calculate the total present value PV1.
PV1 = $70,291.15736 + $362,940.8778 = $433,232.0352 = FV1
This becomes the future value for the second time segment.
For the second time segment:
Step 3: ieq = 0.05165025 remains the same.
Step 4: Calculate the present value PV(2) of step 4 in the first time segment.
PV1 = $433,232.0352 = FV1;
[latex]n=P/Y \times \text{(Number of Years)}=2 \times 6=6[/latex]
[latex]\begin{align} PV_{(2)}&=\frac{FV_1}{(1+i_{eq})^n}\\ &=\frac{\$433,\!232.0352}{(1+0.05165025)^6}\\ &=\$320,\!252.5426 \end{align}[/latex]
Step 5: Apply Formula 7.3B to calculate the present value of the payments.
[latex]\begin{align} PV_{DUE_2}&=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right] \times(1+i_{eq})\\ &=\$50,\!000 \left[\frac{1-(1+0.05165025)^{-6}}{0.05165025}\right] \times(1+0.05165025)\\ &=\$265,\!489.8749 \end{align}[/latex]
Combine steps 4 and 5 to calculate the total present value, PV2.
PV2 = $320,252.5426 + $265,489.8749 = $585,742.42
Therefore, PV2 = PV = $585,742.42
Calculator instructions:
| Time Segment | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| 1 | BGN | 7 | 5.1 | Answer: -433,232.0352 | 60,000 | 100,000 | 1 | 2 |
| 2 | BGN | 6 | 5.1 | Answer: -585,742.4175 | 50,000 | 433,232.0352 | 1 | 2 |
The figure shows how much principal and interest make up the payments. To have his retirement income increased by $10,000 after six years, Rodriguez needs to have $585,742.42 invested in his retirement fund at age 65.
Working with Loans
Solving for a future loan balance is a future value annuity calculation. Therefore, you use the same steps as discussed in Section 7.2. However, you need to modify your interpretation of these steps for loan balances. The figure below helps you understand these differences.

FV1 represents the total amount owing on the loan with interest as if no payments had been made.
FVORD represents the total amount paid against the loan with interest.
With both the FV1 and FVORD on the same focal date, the fundamental concept of the time value of money allows you to then take the FV1 and subtract the FVORD to produce the balance owing on the loan.
Your BAII Plus Calculator
Proper application of the cash flow sign convention for the present value and annuity payment will automatically result in a future value that nets out the loan principal and the payments. Assuming you are the borrower, you enter the present value (PV) as a positive number since you are receiving the money. You enter the annuity payment (PMT) as a negative number since you are paying the money. When you calculate the future value (FV), it displays a negative number, indicating that it is a balance owing.
Concept Check
Example 7.3.4: Balance Owing on a New Truck
Two years ago, Jillian purchased a new Ford F-250 for $71,482.08 with a $5,000 down payment and the remainder financed through her Ford dealership at 5.9% compounded monthly. She has been making monthly payments of $1,282.20. What is her balance owing today? How much interest has she paid to date?
Solution
Step 1: The payments are made at the end of the payment intervals, and the compounding period and payment intervals are the same. Therefore, this is a simple ordinary annuity. Calculate its value two years after its start, which is its future value, or FVORD. Once you know the FVORD, you can determine the amount of interest, or I.
The timeline for the savings annuity appears below.

Step 2: Given information.
PV = $71,482.08 – $5,000 = $66,482.08; I/Y = 5.9%; C/Y = 12; PMT = $1,282.20; P/Y = 12; Years = 2
Step 3: Calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{5.9\%}{12}=0.491\overline{6}\%[/latex]
Step 4: Calculate the balance owing with interest, FV1.
PV=$66,482.08;
[latex]n=P/Y \times \text{(Number of Years)}=12 \times 2=24[/latex]
[latex]FV_1=PV(1+i)^n=\$66,\!482.08(1+0.00491\overline{6})^{24}=\$74,\!786.94231[/latex]
Step 5: Calculate the amount paid with interest, FVORD.
[latex]\begin{align} FV_{ORD}&=PMT \left[ \frac{(1+i)^n-1}{i}\right]\\ &=\$1,\!282.20 \left[ \frac{(1+0.00491\overline{6})^{24}-1}{0.00491\overline{6}}\right]\\ &=\$32,\!577.13179 \end{align}[/latex]
Subtract step 5 from step 4 to calculate the balance still owing, FV.
FV = $74,786.94231 – $32,577.13179 = $42,209.81
Step 6: Calculate the amount of interest.
[latex]\begin{align} I&=(n \times PMT+FV)-PV\\ &=(24 \times \$1,\!282.20+\$42,\!209.81)-\$66,\!482.08\\ &=\$72,\!982.61-\$66,\!482.08\\ &=\$6,\!500.53 \end{align}[/latex]
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 24 | 5.9 | 66482.08 | -1282.2 | Answer: -42,209.81052 | 12 | 12 |
The figure shows how much principal and interest make up the payments. After two years of making monthly payments, Jillian has a balance owing on the Ford F-250 of $42,209.81. Altogether, she has made $30,772.80 in payments, of which $6,500.53 went toward the interest on her loan.
Selling a Loan Contract
Thus, the selling of a loan contract needs to calculate the present value of all remaining annuity payments in the term.

Note: If the final payment is the same as the regular periodic payment you only need to calculate the present value of annuity payments, or PVORD to find the selling price of a loan contract.
Example 7.3.5: Ford Sells the Truck Contract
Continuing with Jillian’s Ford F-250 purchase, recall that Jillian’s monthly payments are fixed at $1,282.20 for five years. Assume that after two years Ford wants to sell the contract to another finance company, which agrees to a discount rate of 10.8% compounded semi-annually. Jillian’s final payment is known at $1,282.49. What are the proceeds of the sale?
Solution
Step 1: The payments are made at the end of the payment intervals, and the compounding period (semi-annually) and payment intervals (monthly) are different. Therefore, this is an ordinary general annuity. Calculate its value on the date of sale, which is its present value, or PVORD, plus the present value of the final payment, or PV1.
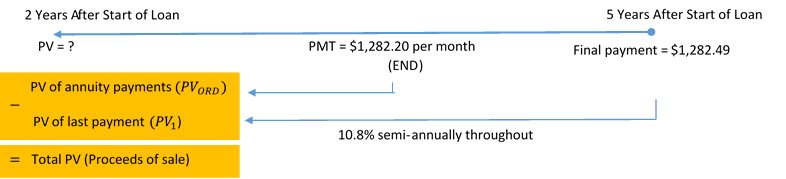
Step 2: Given information.
FV = $1,282.49; I/Y = 10.8%; C/Y = 2; PMT = $1,282.20; P/Y = 12; Years = 3
Step 3: Since P/Y [latex]\ne[/latex] C/Y, calculate the equivalent periodic rate (ieq) that matches the payment interval.
[latex]i=\frac{I/Y}{C/Y}=\frac{10.8\%}{2}=5.4\%[/latex]
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.054)^{\frac{2}{12}}-1=0.008803937\;\text{per month}[/latex]
Step 4: Calculate the present value, PV1, of the last payment.
FV = $1,282.49;
[latex]n=P/Y \times \text{(Number of Years)}=12 \times 3=36[/latex]
[latex]\begin{align} PV_1&=\frac{FV}{(1+i_{eq})^n}\\ &=\frac{\$1,\!282.49}{(1+0.008803937)^{36}}\\ &=\$935.427906 \end{align}[/latex]
Step 5: Apply Formula 7.3A to calculate the present value of the payments, PVORD.
[latex]n=P/Y \times \text{(Number of Years)}=12 \times 3-1=35[/latex]
[latex]\begin{align} PV_{ORD}&=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right]\\ &=\$1,\!282.20\left[\frac{1-(1+0.008803937)^{-35}}{0.008803937}\right]\\ &=\$38,\!477.10711 \end{align}[/latex]
Combine steps 4 and 5 to calculate proceeds of the sale, PV.
PV = $935.427906 + $38,477.10711 = $39,412.51
Calculator instructions:
| Element | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Final Payment | 6 | 10.8 | Answer: -935.427906 | 0 | 1,282.49 | 2 | 2 |
| Annuity | 35 | 10.8 | Answer: -38,477.10711 | 1282.2 | 0 | 12 | 2 |
The figure shows the present value and interest amounts in the transaction. The finance company will pay $39,412.54 for the contract. In return, it receives 35 payments of $1,282.20 and one payment of $1,282.49 for a nominal total of $46,159.49.
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- When Sinbad retires, he expects his RRSP to pay him $2,000 at the end of every month for 25 years. If his retirement annuity earns 3.8% compounded quarterly, how much money does he need to have in his RRSP when he retires?
- Sandy’s parents would like to have an annuity pay her $500 at the beginning of every month from September 1, 2012, to April 1, 2017, to help with her university tuition and living expenses. On May 1, 2017, they would like to give her a graduation gift of $5,000. If the annuity can earn 6.15% compounded quarterly, how much money must be in the account on September 1, 2012? (Use years and months in the calculations)
Note: Solution to exercises are demonstrated using the calculator only.
Timelines for exercises 1 and 2 are included in Solutions to Exercises.
An annuity in which the payment interval equals the compounding interval (P/Y equals to C/Y).
An annuity in which the payment interval does not equal the compounding interval (P/Y does not equal C/Y).

