Maxwell’s Equations: Electromagnetic Waves Predicted and Observed
Lumen Learning
Learning Objective
By the end of this section, you will be able to:
- Restate Maxwell’s equations.

The Scotsman James Clerk Maxwell (1831–1879) is regarded as the greatest theoretical physicist of the 19th century. (See Figure 1.) Although he died young, Maxwell not only formulated a complete electromagnetic theory, represented by Maxwell’s equations, he also developed the kinetic theory of gases and made significant contributions to the understanding of color vision and the nature of Saturn’s rings.
Maxwell brought together all the work that had been done by brilliant physicists such as Oersted, Coulomb, Gauss, and Faraday, and added his own insights to develop the overarching theory of electromagnetism. Maxwell’s equations are paraphrased here in words because their mathematical statement is beyond the level of this text. However, the equations illustrate how apparently simple mathematical statements can elegantly unite and express a multitude of concepts—why mathematics is the language of science.
Maxwell’s Equations
- Electric field lines originate on positive charges and terminate on negative charges. The electric field is defined as the force per unit charge on a test charge, and the strength of the force is related to the electric constant ε0, also known as the permittivity of free space. From Maxwell’s first equation we obtain a special form of Coulomb’s law known as Gauss’s law for electricity.
- Magnetic field lines are continuous, having no beginning or end. No magnetic monopoles are known to exist. The strength of the magnetic force is related to the magnetic constant μ0, also known as the permeability of free space. This second of Maxwell’s equations is known as Gauss’s law for magnetism.
- A changing magnetic field induces an electromotive force (emf) and, hence, an electric field. The direction of the emf opposes the change. This third of Maxwell’s equations is Faraday’s law of induction, and includes Lenz’s law.
- Magnetic fields are generated by moving charges or by changing electric fields. This fourth of Maxwell’s equations encompasses Ampere’s law and adds another source of magnetism—changing electric fields.
Maxwell’s equations encompass the major laws of electricity and magnetism. What is not so apparent is the symmetry that Maxwell introduced in his mathematical framework. Especially important is his addition of the hypothesis that changing electric fields create magnetic fields. This is exactly analogous (and symmetric) to Faraday’s law of induction and had been suspected for some time, but fits beautifully into Maxwell’s equations.
Symmetry is apparent in nature in a wide range of situations. In contemporary research, symmetry plays a major part in the search for sub-atomic particles using massive multinational particle accelerators such as the new Large Hadron Collider at CERN.
Making Connections: Unification of Forces
Maxwell’s complete and symmetric theory showed that electric and magnetic forces are not separate, but different manifestations of the same thing—the electromagnetic force. This classical unification of forces is one motivation for current attempts to unify the four basic forces in nature—the gravitational, electrical, strong, and weak nuclear forces.
Since changing electric fields create relatively weak magnetic fields, they could not be easily detected at the time of Maxwell’s hypothesis. Maxwell realized, however, that oscillating charges, like those in AC circuits, produce changing electric fields. He predicted that these changing fields would propagate from the source like waves generated on a lake by a jumping fish.
The waves predicted by Maxwell would consist of oscillating electric and magnetic fields—defined to be an electromagnetic wave (EM wave). Electromagnetic waves would be capable of exerting forces on charges great distances from their source, and they might thus be detectable. Maxwell calculated that electromagnetic waves would propagate at a speed given by the equation
![]()
When the values for μ0 and ε0 are entered into the equation for c , we find that
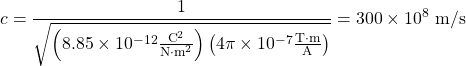
which is the speed of light. In fact, Maxwell concluded that light is an electromagnetic wave having such wavelengths that it can be detected by the eye.
Other wavelengths should exist—it remained to be seen if they did. If so, Maxwell’s theory and remarkable predictions would be verified, the greatest triumph of physics since Newton. Experimental verification came within a few years, but not before Maxwell’s death.
Hertz’s Observations
The German physicist Heinrich Hertz (1857–1894) was the first to generate and detect certain types of electromagnetic waves in the laboratory. Starting in 1887, he performed a series of experiments that not only confirmed the existence of electromagnetic waves, but also verified that they travel at the speed of light.
Hertz used an AC RLC (resistor-inductor-capacitor) circuit that resonates at a known frequency ![]() and connected it to a loop of wire as shown in Figure 2. High voltages induced across the gap in the loop produced sparks that were visible evidence of the current in the circuit and that helped generate electromagnetic waves.
and connected it to a loop of wire as shown in Figure 2. High voltages induced across the gap in the loop produced sparks that were visible evidence of the current in the circuit and that helped generate electromagnetic waves.
Across the laboratory, Hertz had another loop attached to another RLC circuit, which could be tuned (as the dial on a radio) to the same resonant frequency as the first and could, thus, be made to receive electromagnetic waves. This loop also had a gap across which sparks were generated, giving solid evidence that electromagnetic waves had been received.

Hertz also studied the reflection, refraction, and interference patterns of the electromagnetic waves he generated, verifying their wave character. He was able to determine wavelength from the interference patterns, and knowing their frequency, he could calculate the propagation speed using the equation v = fλ (velocity—or speed—equals frequency times wavelength). Hertz was thus able to prove that electromagnetic waves travel at the speed of light. The SI unit for frequency, the hertz (1 Hz = 1 cycle/sec), is named in his honor.
Section Summary
- Electromagnetic waves consist of oscillating electric and magnetic fields and propagate at the speed of light c. They were predicted by Maxwell, who also showed that
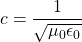 ,
,
where μ0 is the permeability of free space and ε0 is the permittivity of free space. - Maxwell’s prediction of electromagnetic waves resulted from his formulation of a complete and symmetric theory of electricity and magnetism, known as Maxwell’s equations.
- These four equations are paraphrased in this text, rather than presented numerically, and encompass the major laws of electricity and magnetism. First is Gauss’s law for electricity, second is Gauss’s law for magnetism, third is Faraday’s law of induction, including Lenz’s law, and fourth is Ampere’s law in a symmetric formulation that adds another source of magnetism—changing electric fields.
Problems & Exercises
- Verify that the correct value for the speed of light c is obtained when numerical values for the permeability and permittivity of free space (μ0 and ε0) are entered into the equation
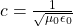 .
. - Show that, when SI units for μ0 and ε0 are entered, the units given by the right-hand side of the equation in the problem above are m/s.
Glossary
electromagnetic waves: radiation in the form of waves of electric and magnetic energy
Maxwell’s equations: a set of four equations that comprise a complete, overarching theory of electromagnetism
RLC circuit: an electric circuit that includes a resistor, capacitor and inductor
hertz: an SI unit denoting the frequency of an electromagnetic wave, in cycles per second
speed of light: in a vacuum, such as space, the speed of light is a constant 3 × 108 m/s
electromotive force (emf): energy produced per unit charge, drawn from a source that produces an electrical current
electric field lines: a pattern of imaginary lines that extend between an electric source and charged objects in the surrounding area, with arrows pointed away from positively charged objects and toward negatively charged objects. The more lines in the pattern, the stronger the electric field in that region
magnetic field lines: a pattern of continuous, imaginary lines that emerge from and enter into opposite magnetic poles. The density of the lines indicates the magnitude of the magnetic field

