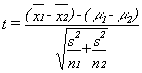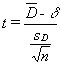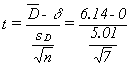5 Chapter 5. The t-Test
In Chapter 3, a sampling distribution, the t-distribution, was introduced. In Chapter 4, you learned how to use the t-distribution to make an important inference, an interval estimate of the population mean. Here you will learn how to use that same t-distribution to make more inferences, this time in the form of hypothesis tests. You will learn how to use the t-test in three different types of hypotheses. You will also have a chance to use the interactive Excel templates to apply the t-test in alternative situations. Before we start to learn about those tests, a quick review of the t-distribution is in order.
The t-distribution
The t-distribution is a sampling distribution. You could generate your own t-distribution with n-1 degrees of freedom by starting with a normal population, choosing all possible samples of one size, n, computing a t-score for each sample, where:
[latex]t = (\bar{x} -\mu)/(s/\sqrt{n})[/latex]
x = the sample mean
μ = the population mean
s = the sample standard deviation
n = the size of the sample
When you have all of the samples’ t-scores, form a relative frequency distribution and you will have your t-distribution. Luckily, you do not have to generate your own t-distributions because any statistics book has a table that shows the shape of the t-distribution for many different degrees of freedom. As introduced in Chapter 2, Figure 5.1 reproduces a portion of a typical t-table within an interactive Excel template.
Figure 5.1 Interactive Excel Template for Determining Cut-off Point of a t-Table – see Appendix 5.
When you look at the formula for the t-score, you should be able to see that the mean t-score is zero because the mean of the x’s is equal to μ. Because most samples have x’s that are close to μ, most will have t-scores that are close to zero. The t-distribution is symmetric, because half of the samples will have x’s greater than μ, and half less. As you can see from the table, if there are 10 df, only .005 of the samples taken from a normal population will have a t-score greater than +3.17. Because the distribution is symmetric, .005 also have a t-score less than -3.17. Ninety-nine per cent of samples will have a t-score between ±3.17. Like the example in Figure 5.1, most t-tables have a picture showing what is in the body of the table. In Figure 5.1, the shaded area is in the right tail, the body of the table shows the t-score that leaves the α in the right tail. This t-table also lists the two-tail α above the one-tail where p = .xx. For 5 df, there is a .05 probability that a sample will have a t-score greater than 2.02, and a .10 probability that a sample will have a t-score either > +2.02 or < -2.02.
There are other sample statistics that follow this same shape and can be used as the basis for different hypothesis tests. You will see the t-distribution used to test three different types of hypotheses in this chapter, and in later chapters, you will see that the t-distribution can be used to test other hypotheses.
Though t-tables show how the sampling distribution of t-scores is shaped if the original population is normal, it turns out that the sampling distribution of t-scores is very close to the one in the table even if the original population is not quite normal, and most researchers do not worry too much about the normality of the original population. An even more important fact is that the sampling distribution of t-scores is very close to the one in the table even if the original population is not very close to being normal as long as the samples are large. This means that you can safely use the t-distribution to make inferences when you are not sure that the population is normal as long as you are sure that it is bell-shaped. You can also make inferences based on samples of about 30 or more using the t-distribution when you are not sure if the population is normal. Not only does the t-distribution describe the shape of the distributions of a number of sample statistics, it does a good job of describing those shapes when the samples are drawn from a wide range of populations, normal or not.
A simple test: Does this sample come from a population with that mean?
Imagine that you have taken all of the samples with n=10 from a population for which you knew the mean, found the t-distribution for 9 df by computing a t-score for each sample, and generated a relative frequency distribution of the t’s. When you were finished, someone brought you another sample (n=10) wondering if that new sample came from the original population. You could use your sampling distribution of t’s to test if the new sample comes from the original population or not. To conduct the test, first hypothesize that the new sample comes from the original population. With this hypothesis, you have hypothesized a value for μ, the mean of the original population, to use to compute a t-score for the new sample. If the t for the new sample is close to zero—if the t-score for the new sample could easily have come from the middle of the t-distribution you generated—your hypothesis that the new sample comes from a population with the hypothesized mean seems reasonable, and you can conclude that the data support the new sample coming from the original population. If the t-score from the new sample is far above or far below zero, your hypothesis that this new sample comes from the original population seems unlikely to be true, for few samples from the original population would have t-scores far from zero. In that case, conclude that the data support the idea that the new sample comes from some other population.
This is the basic method of using this t-test. Hypothesize the mean of the population you think a sample might come from. Using that mean, compute the t-score for the sample. If the t-score is close to zero, conclude that your hypothesis was probably correct and that you know the mean of the population from which the sample came. If the t-score is far from zero, conclude that your hypothesis is incorrect, and the sample comes from a population with a different mean.
Once you understand the basics, the details can be filled in. The details of conducting a hypothesis test of the population mean — testing to see if a sample comes from a population with a certain mean — are of two types. The first type concerns how to do all of this in the formal language of statisticians. The second type of detail is how to decide what range of t-scores implies that the new sample comes from the original population.
You should remember from the last chapter that the formal language of hypothesis testing always requires two hypotheses. The first hypothesis is called the null hypothesis, usually denoted Ho. It states that there is no difference between the mean of the population from which the sample is drawn and the hypothesized mean. The second is the alternative hypothesis, denoted Ha or H1. It states that the mean of the population from which the sample comes is different from the hypothesized value. If your question is “does this sample come from a population with this mean?”, your Ha simply becomes μ ≠ the hypothesized value. If your question is “does this sample come from a population with a mean greater than some value”, then your Ha becomes μ > the hypothesized value.
The other detail is deciding how “close to zero” the sample t-score has to be before you conclude that the null hypothesis is probably correct. How close to zero the sample t-score must be before you conclude that the data support Ho depends on the df and how big a chance you want to take that you will make a mistake. If you decide to conclude that the sample comes from a population with the hypothesized mean only if the sample t is very, very close to zero, there are many samples actually from the population that will have t-scores that would lead you to believe they come from a population with some other mean—it would be easy to make a mistake and conclude that these samples come from another population. On the other hand, if you decide to accept the null hypothesis even if the sample t-score is quite far from zero, you will seldom make the mistake of concluding that a sample from the original population is from some other population, but you will often make another mistake—concluding that samples from other populations are from the original population. There are no hard rules for deciding how much of which sort of chance to take. Since there is a trade-off between the chance of making the two different mistakes, the proper amount of risk to take will depend on the relative costs of the two mistakes. Though there is no firm basis for doing so, many researchers use a 5 per cent chance of the first sort of mistake as a default. The level of chance of making the first error is usually called alpha (α) and the value of alpha chosen is usually written as a decimal fraction — taking a 5 per cent chance of making the first mistake would be stated as α. When in doubt, use α.
If your alternative hypothesis is not equal to, you will conclude that the data support Ha if your sample t-score is either well below or well above zero, and you need to divide α between the two tails of the t-distribution. If you want to use α=.05, you will support Ha if the t is in either the lowest .025 or the highest .025 of the distribution. If your alternative is greater than, you will conclude that the data support Ha only if the sample t-score is well above zero. So, put all of your α in the right tail. Similarly, if your alternative is less than, put the whole α in the left tail.
The table itself can be confusing even after you know how many degrees of freedom you have and if you want to split your α between the two tails or not. Adding to the confusion, not all t-tables look exactly the same. Look at a typical t-table and you will notice that it has three parts: column headings of decimal fractions, row headings of whole numbers, and a body of numbers generally with values between 1 and 3. The column headings are labelled p or area in the right tail, and sometimes α. The row headings are labelled df, but are sometimes labelled ν or degrees of freedom. The body is usually left unlabelled, and it shows the t-score that goes with the α and degrees of freedom of that column and row. These tables are set up to be used for a number of different statistical tests, so they are presented in a way that is a compromise between ease of use in a particular situation and usability for a wide variety of tests. By using the interactive t-table along with the t-distribution provided in Figure 5.1, you will learn how to use other similar tables in any textbook. This template contains two sheets. In one sheet you will see the t-distribution plot, where you can enter your df and choose your level in the yellow cells. The red-shaded area of the upper tail of the distribution will adjust automatically. Alternatively, you can go to the next sheet, where you will have access to the complete version of the t-table. To find the upper tail of the t-distribution, enter df and α level into the yellow cells. The red-shaded area on the graph will adjust automatically, indicating the associated upper tail of the t-distribution.
In order to use the table to test to see if “this sample comes from a population with a certain mean,” choose α and find the number of degrees of freedom. The number of degrees of freedom in a test involving one sample mean is simply the size of the sample minus one (df = n-1). The α you choose may not be the α in the column heading. The column headings show the right tail areas—the chance you’ll get a t-score larger than the one in the body of the table. Assume that you had a sample with ten members and chose α = .05. There are nine degrees of freedom, so go across the 9 df row to the .025 column since this is a two-tail test, and find the t-score of 2.262. This means that in any sampling distribution of t-scores, with samples of ten drawn from a normal population, only 2.5 per cent (.025) of the samples would have t-scores greater than 2.262—any t-score greater than 2.262 probably occurs because the sample is from some other population with a larger mean. Because the t-distributions are symmetrical, it is also true that only 2.5 per cent of the samples of ten drawn from a normal population will have t-scores less than -2.262. Putting the two together, 5 per cent of the t-scores will have an absolute value greater the 2.262. So if you choose α=.05, you will probably be using a t-score in the .025 column. The picture that is at the top of most t-tables shows what is going on. Look at it when in doubt.
LaTonya Williams is the plant manager for Eileen’s Dental Care Company (EDC), which makes dental floss in Toronto, Ontario. EDC has a good, stable workforce of semi-skilled workers who package floss, and are paid by piecework. The company wants to make sure that these workers are paid more than the local average wage. A recent report by the local Chamber of Commerce shows an average wage for machine operators of $11.71 per hour. LaTonya must decide if a raise is needed to keep her workers above the average. She takes a sample of workers, pulls their work reports, finds what each one earned last week, and divides their earnings by the hours they worked to find average hourly earnings. Those data appear in Table 5.1.
| Worker | Wage (dollars/hour) |
|---|---|
| Smith | 12.65 |
| Wilson | 12.67 |
| Peterson | 11.9 |
| Jones | 10.45 |
| Gordon | 13.5 |
| McCoy | 12.95 |
| Bland | 11.77 |
LaTonya wants to test to see if the mean of the average hourly earnings of her workers is greater than $11.71. She wants to use a one-tail test because her question is greater than not unequal to. Her hypotheses are:
[latex]H_o: \mu \leq \$11.71\;and\;H_a: \mu > \$11.71[/latex]
As is usual in this kind of situation, LaTonya is hoping that the data support Ha, but she wants to be confident that it does before she decides her workers are earning above average wages. Remember that she will compute a t-score for her sample using $11.71 for μ. If her t-score is negative or close to zero, she will conclude that the data support Ho. Only if her t-score is large and positive will she go with Ha. She decides to use α=.025 because she is unwilling to take much risk of saying the workers earn above average wages when they really do not. Because her sample has n=7, she has 6 df. Looking at the table, she sees that the data will support Ha, the workers earn more than average, only if the sample t-score is greater than 2.447.
Finding the sample mean and standard deviation, x = $10.83 and s = $.749, LaTonya computes her sample t-score:
[latex]t=(\bar{x}-\mu)/(s/\sqrt{n})=(10.83-11.71)/(.749/\sqrt{7})=1.48[/latex]
Because her sample t is not greater than +2.447, the H0 is not rejected, indicating that LaTonya concludes that she will have to raise the piece rates EDC pays in order to be really sure that mean hourly earnings are above the local average wage.
If LaTonya had simply wanted to know if EDC’s workers earned the same as other workers in the area, she would have used a two-tail test. In that case, her hypotheses would have been:
[latex]H_o: \mu = \$11.71\;and\;H_a: \mu \neq \$11.71[/latex]
Using α=.10, LaTonya would split the .10 between the two tails since the data support Ha if the sample t-score is either large and negative or large and positive. Her arithmetic is the same, her sample t-score is still 1.41, but she now will decide that the data support Ha only if it is outside ±1.943. In this case, LaTonya will again reject H0, and conclude that the EDC’s workers do not earn the same as other workers in the area.
An alternative to choosing an alpha
Many researchers now report how unusual the sample t-score would be if the null hypothesis were true rather than choosing an α and stating whether the sample t-score implies the data support one or the other of the hypotheses based on that α. When a researcher does this, he is essentially letting the reader of his report decide how much risk to take of making which kind of mistake. There are even two ways to do this. If you look at a portion of any textbook t-table, you will see that it is not set up very well for this purpose; if you wanted to be able to find out what part of a t-distribution was above any t-score, you would need a table that listed many more t-scores. Since the t-distribution varies as the df. changes, you would really need a whole series of t-tables, one for each df. Fortunately, the interactive Excel template provided in Figure 5.1 will enable you to have a complete picture of the t-table and its distribution.
The old-fashioned way of making the reader decide how much of which risk to take is to not state an α in the body of your report, but only give the sample t-score in the main text. To give the reader some guidance, you look at the usual t-table and find the smallest α, say it is .01, that has a t-value less than the one you computed for the sample. Then write a footnote saying, “The data support the alternative hypothesis for any α > .01.”
The more modern way uses the capability of a computer to store lots of data. Many statistical software packages store a set of detailed t-tables, and when a t-score is computed, the package has the computer look up exactly what proportion of samples would have t-scores larger than the one for your sample. Table 5.2 shows the computer output for LaTonya’s problem from a typical statistical package. Notice that the program gets the same t-score that LaTonya did, it just goes to more decimal places. Also notice that it shows something called the p-value. The p-value is the proportion of t-scores that are larger than the one just computed. Looking at the example, the computed t statistic is 1.48 and the p-value is .094. This means that if there are 6 df, a little more than 9 per cent of samples will have a t-score greater than 1.48. Remember that LaTonya used an α = .025 and decided that the data supported Ho, the p-value of .094 means that Ho, would be supported for any α less than .094. Since LaTonya had used α = .025, this p-value means she does not find support for Ho.
| Hypothesis test: Mean |
| Null hypothesis: Mean = $11.71 |
| Alternative: greater than |
| Computed t statistic = 1.48 |
| p-value = .094 |
The p-value approach is becoming the preferred way to present research results to audiences of professional researchers. Most of the statistical research conducted for a business firm will be used directly for decision making or presented to an audience of executives to aid them in making a decision. These audiences will generally not be interested in deciding for themselves which hypothesis the data support. When you are making a presentation of results to your boss, you will want to simply state which hypothesis the evidence supports. You may decide by using either the traditional α approach or the more modern p– value approach, but deciding what the evidence says is probably your job.
Another t-test: do these two (independent) samples come from populations with the same mean?
One of the other statistics that has a sampling distribution that follows the t-distribution is the difference between two sample means. If samples of one size (n1) are taken from one normal population and samples of another size (n2) are taken from another normal population (and the populations have the same standard deviation), then a statistic based on the difference between the sample means and the difference between the population means is distributed like t with n1 + n2 – 2 degrees of freedom. These samples are independent because the members in one sample do not affect which members are in the other sample. You can choose the samples independently of each other, and the two samples do not need to be the same size. The t-statistic is:
where
xi = the mean of sample i
μi = the mean of population i
s2 = the pooled variance
ni = the size of sample i
The usual case is to test to see if the samples come from populations with the same mean, the case where (μ1 – μ2) = 0. The pooled variance is simply a weighted average of the two sample variances, with the weights based on the sample sizes. This means that you will have to calculate the pooled variance before you calculate the t-score. The formula for pooled variance is:
To use the pooled variance t-score, it is necessary to assume that the two populations have equal variances. If you are wondering about why statisticians make a strong assumption in order to use such a complicated formula, it is because the formula that does not need the assumption of equal variances is even more complicated, and reduces the degrees of freedom in the final statistic. In any case, unless you have small samples, the amount of arithmetic needed means that you will probably want to use a statistical software package for this test. You should also note that you can test to see if two samples come from populations that are any hypothesized distance apart by setting (μ1 – μ2) equal to that distance.
In a report published in a 2001 issue of University Affairs,[1] Frank claimed that researchers found a drop in the number of students getting low grades in most courses, and an increase in the number getting high grades (Frank, 2001). This issue is also known as grade inflation. Nora Alston chairs the Economics Department at Oaks College, and the Dean has sent her a copy of the report with a note attached saying, “Is this true here at Oaks? Let me know.” Dr. Alston is not sure if the Dean would be happier if economics grades were higher or lower than other grades, but the report claims that economics grades are lower. Her first stop is the Registrar’s office.
She has the clerk in that office pick a sample of 10 class grade reports from across the college spread over the past three semesters. She also has the clerk pick out a sample of 10 reports for economics classes. She ends up with a total of 38 grades for economics classes and 51 grades for other classes. Her hypotheses are:
[latex]H_o: \mu_{econ} - \mu_{other} \geq 0[/latex]
[latex]H_a: \mu_{econ} - \mu_{other} < 0[/latex] She decides to use α = .05$ .
This is a lot of data, and Dr. Alston knows she will want to use the computer to help. She initially thought she would use a spreadsheet to find the sample means and variances, but after thinking a minute, she decided to use a statistical software package. The one she is most familiar with is called SAS. She loads SAS onto her computer, enters the data, and gives the proper SAS commands. The computer gives her the output shown in Table 5.3.
| Table 5.3 The SAS System Software Output for Dr. Alston’s Grade Study | ||||||
| TTFST Procedure | ||||||
| Variable: GRADE | ||||||
| Dept | N | Mean | Dev | Std Error | Minimum | Maximum |
| Econ | 38 | 2.28947 | 1.01096 | .16400 | 0 | 4.00000 |
| Variance | t | df | Prob>[t] |
| Unequal | -2.3858 | 85.1 | .0193 |
| Equal | -2.3345 | 87.0 | .0219 |
| For Ho: Variances are equal, f=1.35, df[58.37], Prob>f=.3485 | |||
Dr. Alston has 87 df, and has decided to use a one-tailed, left tail test with α = .05$. She goes to her t-table and finds that 87 df does not appear, the table skipping from 60 to 120 df. There are two things she could do. She could try to interpolate the t-score that leaves .05 in the tail with 87 df, or she could choose between the t-value for 60 and 120 in a conservative manner. Using the conservative choice is the best initial approach, and looking at her table she sees that for 60 df .05 of t-scores are less than -1.671,and for 120 df, .05 are less than -1.658. She does not want to conclude that the data support economics grades being lower unless her sample t-score is far from zero, so she decides that she will accept Ha if her sample t is to the left of -1.671. If her sample t happens to be between -1.658 and -1.671, she will have to interpolate.
Looking at the SAS output, Dr. Alston sees that her t-score for the equal variances formula is -2.3858, which is well below -1.671. She concludes that she will tell the Dean that economics grades are lower than grades elsewhere at Oaks College.
Notice that SAS also provides the t-score and df for the case where equal variances are not assumed in the unequal line. SAS also provides a p-value, but it is for a two-tail test because it gives the probability that a t with a larger absolute value, >|T|, occurs. Be careful when using the p-values from software: notice if they are one-tail or two-tail p-values before you make your report.
A third t-test: do these (paired) samples come from the sample population?
Managers are often interested in before and after questions. As a manager or researcher, you will often want to look at longitudinal studies, studies that ask about what has happened to an individual as a result of some treatment or across time. Are they different after than they were before? For example, if your firm has conducted a training program, you will want to know if the workers who participated became more productive. If the work area has been rearranged, do workers produce more than before? Though you can use the difference of means test developed earlier, this is a different situation. Earlier, you had two samples that were chosen independently of each other; you might have a sample of workers who received the training and a sample of workers who had not. The situation for this test is different; now you have a sample of workers, and for each worker, you have measured their productivity before the training or rearrangement of the work space, and you have measured their productivity after. For each worker, you have a pair of measures, before and after. Another way to look at this is that for each member of the sample you have a difference between before and after.
You can test to see if these differences equal zero, or any other value, because a statistic based on these differences follows the t-distribution for n-1 df when you have n matched pairs. That statistic is:
where
D = the mean of the differences in the pairs in the sample
δ = the mean of the differences in the pairs in the population
sD = the standard deviation of the differences in the sample
n = the number of pairs in the sample
It is a good idea to take a minute and figure out this formula. There are paired samples, and the differences in those pairs, the D’s, are actually a population. The mean of those D’s is δ. Any sample of pairs will also yield a sample of D’s. If those D’s are normally distributed, then the t-statistic in the formula above will follow the t-distribution. If you think of the D’s as being the same as x’s in the t-formula at the beginning of the chapter, and think of δ as the population mean, you should realize that this formula is really just that basic t formula.
Lew Podolsky is division manager for Dairyland Lighting, a manufacturer of outdoor lights for parking lots, barnyards, and playing fields. Dairyland Lighting organizes its production work by teams. The size of the team varies somewhat with the product being assembled, but there are usually three to six in a team, and a team usually stays together for a few weeks assembling the same product. Dairyland Lighting has two new plants: one in Oshawa, Ontario, and another in Osoyoos, British Columbia, that serves their Canadian west coast customers. Lew has noticed that productivity seems to be lower in Osoyoos during the summer, a problem that does not occur at their plant in Oshawa. After visiting the Osoyoos plant in July, August, and November, and talking with the workers during each visit, Lew suspects that the un-air-conditioned plant just gets too hot for good productivity. Unfortunately, it is difficult to directly compare plant-wide productivity at different times of the year because there is quite a bit of variation in the number of employees and the product mix through the year. Lew decides to see if the same workers working on the same products are more productive on cool days than hot days by asking the local manager, Dave Mueller, to find a cool day and a hot day from the previous fall and choose ten work teams who were assembling the same products on the two days. Dave sends Lew the data found in Table 5.4.
| Team leader | Output—cool day | Output—hot day | Difference (cool-hot) |
|---|---|---|---|
| November 14 | July 20 | ||
| Martinez | 153 | 149 | 4 |
| McAlan | 167 | 170 | -3 |
| Wilson | 164 | 155 | 9 |
| Burningtree | 183 | 179 | 4 |
| Sanchez | 177 | 167 | 10 |
| Lilly | 162 | 150 | 12 |
| Cantu | 165 | 158 | 7 |
Lew decides that if the data support productivity being higher on cool days, he will call in a heating/air-conditioning contractor to get some cost estimates so that he can decide if installing air conditioning in the Osoyoos plant is cost effective. Notice that he has matched pairs data — for each team he has production on November 14, a cool day, and on July 20, a hot day. His hypotheses are:
[latex]H_o: \delta \leq 0\;and\;H_a: \delta > 0[/latex]
Using α = .05 in this one-tail test, Lew will decide to call the engineer if his sample t-score is greater than 1.943, since there are 6 df. Using the interactive Excel template in Figure 5.2, Lew finds:
and his sample t-score is
Figure 5.2 Interactive Excel Template for Paired t-Test - see Appendix 5.
All these calculations can also be done in the interactive Excel template in Figure 5.2. You can add the two columns of data for cool and hot days and set your α level. The associated t-distribution will automatically adjust based on your data and the selected level of α. You can also see the p-value in the dark blue, and the selected α in the red-shaded areas on this graph. Because his sample t-score is greater than 1.943, or the p-value is less than the alpha, Lew gets out the telephone book and looks under air conditioning contractors to call for some estimates.
Summary
The t-tests are commonly used hypothesis tests. Researchers often find themselves in situations where they need to test to see if a sample comes from a certain population, and therefore test to see if the sample probably came from a population with that certain mean. Even more often, researchers will find themselves with two samples and want to know if the samples come from the same population, and will test to see if the samples probably come from populations with the same mean. Researchers also frequently find themselves asking if two sets of paired samples have equal means. In any case, the basic strategy is the same as for any hypothesis test. First, translate the question into null and alternative hypotheses, making sure that the null hypothesis includes an equal sign. Second, choose α. Third, compute the relevant statistics, here the t-score, from the sample or samples. Fourth, using the tables, decide if the sample statistic leads you to conclude that the sample came from a population where the null hypothesis is true or a population where the alternative is true.
The t-distribution is also used in testing hypotheses in other situations since there are other sampling distributions with the same t-distribution shape. So, remember how to use the t-tables for later chapters.
Statisticians have also found how to test to see if three or more samples come from populations with the same mean. That technique is known as one-way analysis of variance. The approach used in analysis of variance is quite different from that used in the t-test. It will be covered in Chapter 6.
- Frank, T. (2001, February). New study says grades are inflated at Ontario universities. University Affairs, 29. ↵