1 Review of the Basics
Chapter 1 Topics
1.1 Algebraic Expressions
1.2 Linear Equations—Manipulating and Solving
1.3 Natural Logarithms
Where can you go in life and not be exposed to numbers and mathematics? Whether you are figuring out the price of a product (including shipping) on eBay, or balancing your bank accounts, you use your elementary mathematical skills from both your primary and secondary education.
Think about the math you perform every day:
- At the grocery store, you compare products to calculate the best value. One brand of potato chips retails for $3.99 for 300 g, while the equally satisfying brand beside it is priced at $3.49 for 250 g. Which offers the better value?
- As the host for a large gathering, you are preparing a homemade lasagna and need to triple the original recipe, which calls for 1 ⅔ cups of tomato sauce. In the expanded recipe, how many cups of tomato sauce do you need?
- If you are a sports fan, you know plenty of statistics about your favourite players and teams. Many come in percentage form, such as three-point throws for NBA stars or save percentages for NHL goaltenders. What exactly do those percentages mean?
- Many employers pay out bonuses. Perhaps in your company managers get twice as large a bonus as employees. Your company has five managers and 25 employees. If it announces a $35,000 total bonus, what is your share as an employee?
Mathematics and numbers surround you in the business world, where you must read many numerical reports, interpret how the numbers fit together, and create your own reports showing such metrics as sales and profit projections.
Away from work, you must manage your income and pay your bills. This is a mathematical problem you likely solve on a daily basis, ensuring that the money flowing out of your bank account does not exceed the money flowing in. To purchase groceries, vacations, or entertainment, you need numbers.
This chapter gives you a refresher on your basic mathematical skills, which are essential for success in later chapters. Some instructors will review this chapter with you, while others will leave it up to you to complete this chapter independently. Either way, this chapter is important and should be used to test your basic abilities. For example, it would be unfortunate if you got a leasing calculation wrong because you made an error by breaking an order of operation rule even though you understood basic leasing concepts.
Approach this chapter with confidence, and if you encounter any difficulties ensure that you master the concepts before moving on to future chapters.
1.1 Algebraic Expressions
If you are like most Canadians, your employer pays you biweekly. Assume you earn $12.00 per hour. How do you calculate your pay cheque every pay period? Your earnings are calculated as follows:
$12.00 × (Hours worked during the biweekly pay period)
The hours worked during the biweekly pay period is the unknown variable. Notice that the expression appears lengthy when you write out the explanation for the variable. Algebra is a way of making such expressions more convenient to manipulate. To shorten the expression, making it easier to read, algebra assigns a letter or group of letters to represent the variable. In this case, you might choose h to represent “hours worked during the biweekly pay period.” This rewrites the above expression as follows:
$12.00 × h or $12h
Unfortunately, the word algebra makes many people’s eyes glaze over. But remember that algebra is just a way of solving a numerical problem. It demonstrates how the pieces of a puzzle fit together to arrive at a solution.
For example, you have used your algebraic skills if you have ever programmed a formula into Microsoft Excel. You told Excel there was a relationship between cells in your spreadsheet. Perhaps your calculation required cell A3 to be divided by cell B6 and then multiplied by cell F2. This is an algebraic equation. Excel then took your algebraic equation and calculated a solution by automatically substituting in the appropriate values from the referenced cells (your variables).
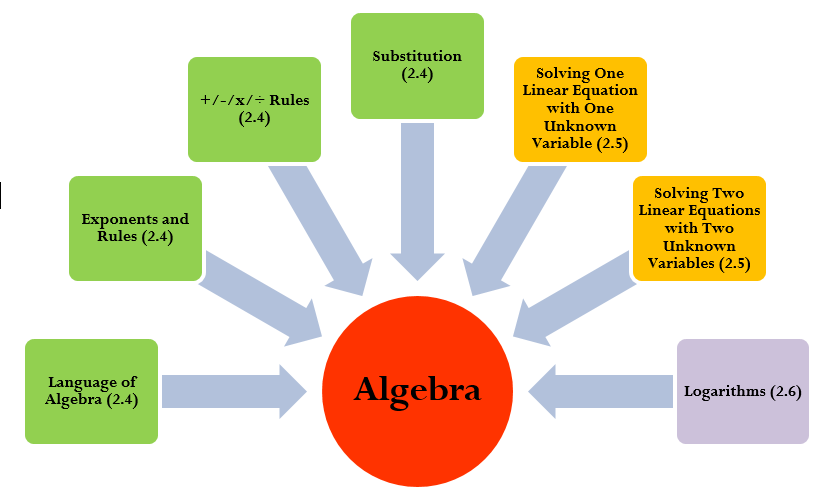
As illustrated in the figure to the right, algebra involves integrating many interrelated concepts. This figure shows only the concepts that are important to business mathematics, which this textbook will present piece by piece. Your understanding of algebra will become more complete as more concepts are covered over the course of this book.
This section reviews the language of algebra, exponent rules, basic operation rules, and substitution. In Section 2.5 you will put these concepts to work in solving one linear equation for one unknown variable along with two linear equations with two unknown variables. Finally, in Section 2.6 you will explore the concepts of logarithms and natural logarithms.
The Language of Algebra
Understanding the rules of algebra requires familiarity with four key definitions.
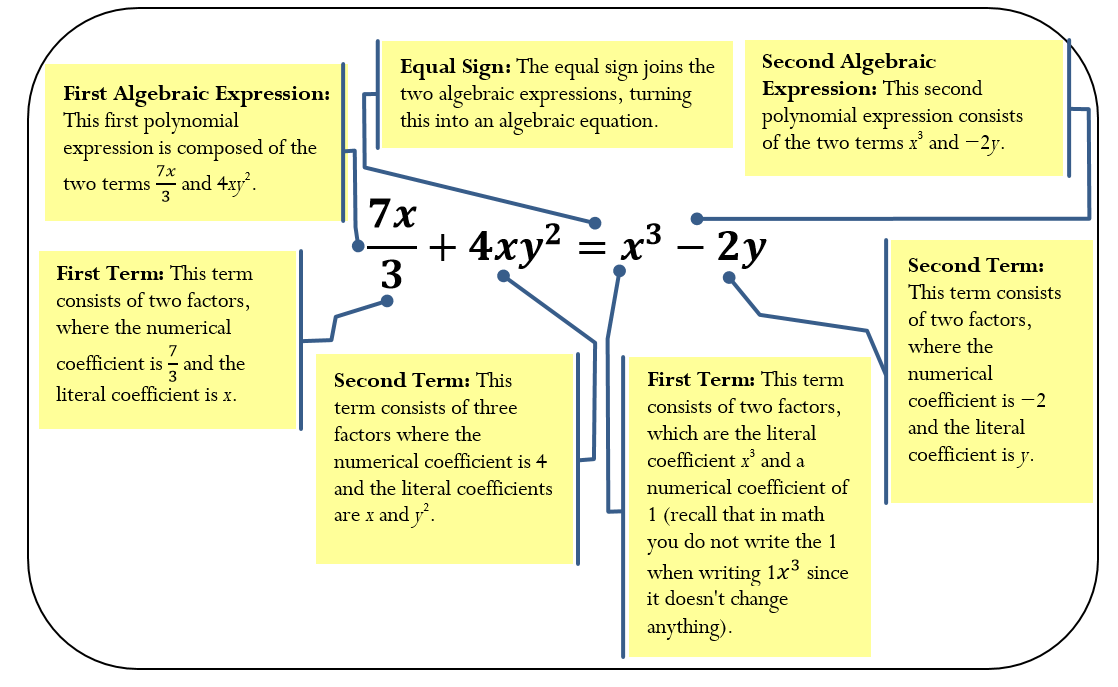
Algebraic Expression
A mathematical algebraic expression indicates the relationship between and mathematical operations that must be conducted on a series of numbers or variables. For example, the expression $12h says that you must take the hourly wage of $12 and multiply it by the hours worked. Note that the expression does not include an equal sign, or “=”. It only tells you what to do and requires that you substitute a value in for the unknown variable(s) to solve. There is no one definable solution to the expression.
Algebraic Equation
A mathematical algebraic equation takes two algebraic expressions and equates them. This equation can be solved to find a solution for the unknown variables. Examine the following illustration to see how algebraic expressions and algebraic equations are interrelated.
Algebraic Equation

Term
In any algebraic expression, terms are the components that are separated by addition and subtraction. In looking at the example above, the expression 6x + 3y is composed of two terms. These terms are “6x” and “3y.” A nomial refers to how many terms appear in an algebraic expression. If an algebraic expression contains only one term, like “$12.00h,” it is called a monomial. If the expression contains two terms or more, such as “6x + 3y,” it is called a polynomial.
Factor
Terms may consist of one or more factors that are separated by multiplication or division signs. Using the 6x from above, it consists of two factors. These factors are “6” and “x”; they are joined by multiplication.
- If the factor is numerical, it is called the numerical coefficient.
- If the factor is one or more variables, it is called the literal coefficient
Factors
Exponents
Exponents are widely used in business mathematics and are integral to financial mathematics. When applying compounding interest rates to any investment or loan, you must use exponents.
Exponents are a mathematical shorthand notation that indicates how many times a quantity is multiplied by itself. The format of an exponent is illustrated below.
Exponents
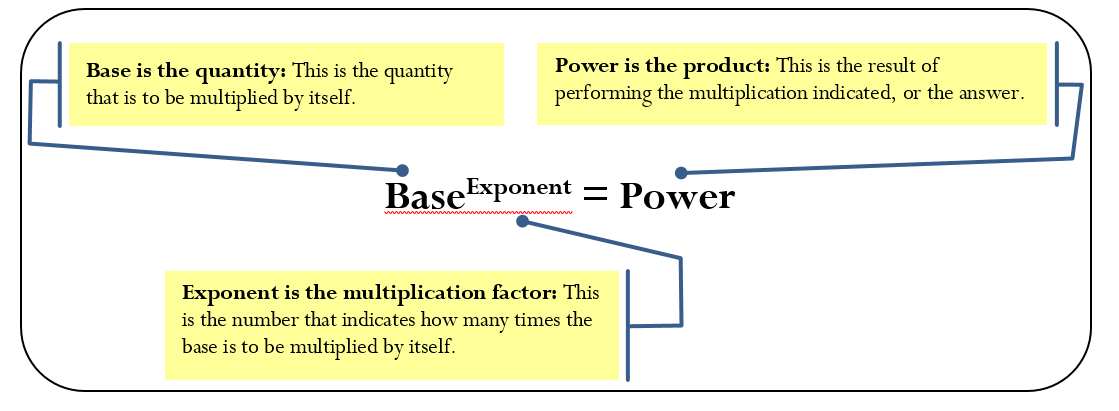
Assume you have 23 = 8. The exponent of 3 says to take the base of 2 multiplied by itself three times, or 2 × 2 × 2. The power is 8. The proper way to state this expression is “2 to the exponent of 3 results in a power of 8.”
How It Works
Many rules apply to the simplification of exponents, as shown in the table below.
| Rule | Illustration | Explanation |
| 1. Multiplication | ya × yb = ya+b | If the bases are identical, add the exponents and retain the unchanged base. |
| 2. Division | If the bases are identical, subtract the exponents and retain the unchanged base. | |
| 3. Raising powers to exponents | (ybzc)a = yb×azc×a
or
|
If a single term is raised to an exponent, each factor must retain its base and you must multiply the exponents for each by the raised exponent. Note that if the expression inside the brackets has more than one term, such as (yb + zc)a, which has two terms, you cannot multiply the exponent a inside the brackets. |
| 4. Zero exponents | y0 = 1
|
Any base to a zero exponent will always produce a power of 1. This is explained later in this section when you review the concept of algebraic division. |
| 5. Negative exponents | y−a = |
The negative sign indicates that the power has been shifted between the numerator and denominator. It is commonly used in this textbook to simplify appearances. Note that on the BAII Plus calculator, keying in a negative exponent requires you to key in the value of y, press yx, enter the value of a, press ±, and then press = to calculate. |
| 6. Fractional exponents | A fractional exponent is a different way of writing a radical sign. Note that the base is first taken to the exponent of a, then the root of b is found to get the power. For example, This is the same as . To key in a fractional exponent on the BAII Plus calculator, input the value of y, press yx, open a set of brackets, key in a ÷ b, close the brackets, and press = to calculate. |
Important Notes
Recall that mathematicians do not normally write the number 1 when it is multiplied by another factor because it doesn’t change the result. The same applies to exponents. If the exponent is a 1, it is generally not written because any number multiplied by itself only once is the same number. For example, the number 2 could be written as 21, but the power is still 2. Or take the case of (yz)a. This could be written as (y1z1)a, which when simplified becomes (y1×az1)a or yaza. Thus, even if you don’t see an exponent written, you know that the value is 1.
Example 1.1A Exponents in Algebra
[table id=2 /]
Addition and Subtraction
Simplification of unnecessarily long or complex algebraic expressions is always preferable to increase understanding and reduce the chances of error. For example, assume you are a production manager looking to order bolts for a product that you make. Your company makes three products, all in equal quantity. Product A requires seven bolts, Product B requires four bolts, and Product C requires fourteen bolts. If q represents the quantity of products required, you need to order 7q + 4q + 14q bolts. This expression requires four calculations to solve every time (each term needs to be multiplied by q and you then need to add everything together). With the algebra rules that follow, you can simplify this expression to 25q. This requires only one calculation to solve. So what are the rules?
How It Works
In math, terms with the same literal coefficients are called like terms. Only terms with the identical literal coefficients may be added or subtracted through the following procedure:
Step 1: Simplify any numerical coefficients by performing any needed mathematical operation or converting fractions to decimals. For example, terms such as ![]() should become 0.5y.
should become 0.5y.
Step 2: Add or subtract the numerical coefficients of like terms as indicated by the operation while obeying the rules of BEDMAS.
Step 3: Retain and do not change the common literal coefficients. Write the new numerical coefficient in front of the retained literal coefficients.
From the previous example, you require 7q + 4q + 14q bolts. Notice that there are three terms, each of which has the same literal coefficient. Therefore, you can perform the required addition.
Step 1: All numerical coefficients are simplified already. Skip to step 2.
Step 2: Take the numerical coefficients and add the numbers: 7 + 4 + 14 equals 25.
Step 3: Retain the literal coefficient of q. Put the new numerical coefficient and literal coefficient together. Thus, 25q. Therefore 7q + 4q + 14q is the same as 25q.
Things To Watch Out For
A common mistake in addition and subtraction is combining terms that do not have the same literal coefficient. You need to remember that the literal coefficient must be identical. For example, 7q and 4q have the identical literal coefficient of q. However, 7q and 4q2 have different literal coefficients, q and q2, and cannot be added or subtracted.
Paths To Success
Remember that if you come across a literal coefficient with no number in front of it, that number is assumed to be a 1. For example, x has no written numerical coefficient, but it is the same as 1x. Another example would be ![]() is the same as
is the same as ![]() or
or ![]() .
.
On a similar note, mathematicians also don’t write out literal coefficients that have an exponent of zero. For example, 7x0 is just 7(1) or 7. Thus, the literal coefficient is always there; however, it has an exponent of zero. Remembering this will help you later when you multiply and divide in algebra.
Give It Some Thought
Examine the following algebraic expressions and indicate how many terms can be combined through addition and subtraction. No calculations are necessary. Do not attempt to simplify.
Solutions:
- Three terms (all of the x)
- Four terms (all of the g2)
Example 1.1B: Addition and Subtraction in Algebra
[table id=3 /]
Multiplication
How It Works
Follow these steps to multiple algebraic expressions:
Step 1: Check to see if there is any way to simplify the algebraic expression first. Are there any like terms you can combine? For example, you can simplify (3x + 2 + 1)(x + x + 4) to (3x + 3)(2x + 4) before attempting the multiplication.
Step 2: Take every term in the first algebraic expression and multiply it by every term in the second algebraic expression. This means that numerical coefficients in both terms are multiplied by each other, and the literal coefficients in both terms are multiplied by each other. It is best to work methodically from left to right so that you do not miss anything. Working with the example, in (3x + 3)(2x + 4) take the first term of the first expression, 3x, and multiply it by 2x and then by 4. Then move to the second term of the first expression, 3, and multiply it by 2x and then by 4 (see the figure).
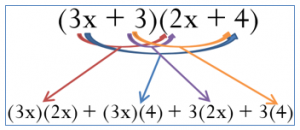
It becomes: 6x2 + 12x + 6x + 12
Step 3: Perform any final steps of simplification by adding or subtracting like terms as needed. In the example, two terms contain the literal coefficient x, so you simplify the expression to 6x2 + 18x + 12.
Important Notes
If the multiplication involves more than two expressions being multiplied by each other, it is easiest to work with only one pair of expressions at a time starting with the leftmost pair. For example, if you are multiplying (4x + 3)(3x)(9y + 5x), resolve (4x + 3)(3x) first. Then take the solution, keeping it in brackets since you have not completed the math operation, and multiply it by (9y + 5x). This means you are required to repeat step 2 in the multiplication procedure until you have resolved all the multiplications.
Things To Watch Out For
The negative sign causes no end of grief for a lot of people when working with multiplication. First, if a numerical coefficient is not written explicitly, it is assumed to be 1. For example, look at 2(4a + 6b) − (2a − 3b). This is the same as 2(4a + 6b) + (−1)(2a − 3b).
When you multiply a negative through an expression, all signs in the brackets will change. Continuing with the second term in the above example, −(2a − 3b) becomes −2a + 3b. The expression then looks like 2(4a + 6b) − 2a + 3b.
Paths To Success
The order in which you write the terms of an algebraic expression does not matter so long as you follow all the rules of BEDMAS. For example, whether you write 3 × 4 or 4 × 3, the answer is the same because you can do multiplication in any order. The same applies to 4 + 3 – 1 or 3 – 1 + 4. Now let’s get more complex. Whether you write 3x2 + 5x – 4 or 5x – 4 + 3x2, the answer is the same as you have not violated any rules of BEDMAS. You still multiply first and add last from left to right.
Although the descending exponential format for writing expressions is generally preferred, for example, 3x2 + 5x + 4, which lists literal coefficients with higher exponents first, it does not matter if you do this or not. When checking your solutions against those given in this textbook, you only need to ensure that each of your terms matches the terms in the solution provided.
Example 1.1C: Algebraic Multiplication
[table id=4 /]
Division
You are often required to divide a monomial into either a monomial or a polynomial. In instances where the denominator consists of a polynomial, it is either not possible or extremely difficult to simplify the expression algebraically. Only division where denominators are monomials are discussed here.
How It Works
To simplify an expression when its denominator is a monomial, apply these rules:
Step 1: Just as in multiplication, determine if there is any way to combine like terms before completing the division. For example, with ![]() you can simplify the numerator to
you can simplify the numerator to ![]()
Step 2: Take every term in the numerator and divide it by the term in the denominator. This means that you must divide both the numerical and the literal coefficients. As with multiplication, it is usually best to work methodically from left to right so that you do not miss anything. So in our example we get:
![]()
(2)(1)(1) − (1)(a)(1) + (3)(1)(b)
2 − a + 3b
Step 3: Perform any final simplification by adding or subtracting the like terms as needed. As there are no more like terms, the final expression remains 2 − a + 3b.
You may have heard of an outcome called “cancelling each other out.” For example, in resolving the division ![]() many people would say that the terms cancel each other out. Many people will also mistakenly interpret this to mean that the quotient is zero and say that
many people would say that the terms cancel each other out. Many people will also mistakenly interpret this to mean that the quotient is zero and say that ![]() %. In fact, when terms cancel each other out the quotient is one, not zero. The numerical coefficient is
%. In fact, when terms cancel each other out the quotient is one, not zero. The numerical coefficient is ![]() . The literal coefficient is
. The literal coefficient is ![]() Thus,
Thus, ![]() . This also explains why a zero exponent equals one:
. This also explains why a zero exponent equals one: ![]() .
.
Paths To Success
A lot of people dislike fractions and find them hard to work with. Remember that when you are simplifying any algebraic expression you can transform any fraction into a decimal. For example, if your expression is ![]() , you can convert the fraction into decimals: 0.4x + 0.75x. In this format, it is easier to solve.Substitution
, you can convert the fraction into decimals: 0.4x + 0.75x. In this format, it is easier to solve.Substitution
The ultimate goal of algebra is to represent a relationship between various variables. Although it is beneficial to simplify these relationships where possible and shorten the algebraic expressions, in the end you want to calculate a solution. Substitution involves replacing the literal coefficients of an algebraic expression with known numerical values. Once the substitution has taken place, you solve the expression for a final value.
Example 1.1 D
[table id=5 /]
How It Works
Follow these steps to perform algebraic substitution:
Step 1: Identify the value of your variables. Assume the algebraic equation is ![]() . You need to calculate the value of PV. It is known that FV = $5,443.84, r = 0.12, and t =
. You need to calculate the value of PV. It is known that FV = $5,443.84, r = 0.12, and t = ![]() .
.
Step 2: Take the known values and insert them into the equation where their respective variables are located, resulting in ![]() .
.
Step 3: Resolve the equation to solve for the variable. Calculate ![]()
Things To Watch Out For
It is common in algebra to represent a variable with more than just one letter. As you can see from the example above, FV is a variable, and it represents future value. This should not be interpreted to be two variables, F and V. Similarly, PMT represents annuity payment. When you learn new formulas and variables, take careful note of how a variable is represented.
As well, some literal coefficients have subscripts. For example, you could see d1 and d2 in the same formula. What sometimes happens is that there is more than one value for the same variable. As you will learn in Chapter 6 about merchandising, when you buy an item you may receive more than one discount rate (what d stands for). Therefore, the first discount gets a subscript of 1, or d1, and the second discount gets a subscript of 2, or d2. This allows you to distinguish between the two values in the equation and substitute the correct value in the correct place.
Paths To Success
If you are unsure whether you have simplified an expression appropriately, remember that you can make up your own values for any literal coefficient and substitute those values into both the original and the simplified expressions. If you have obeyed all the rules and simplified appropriately, both expressions will produce the same answer. For example, assume you simplified 2x + 5x into 7x, but you are not sure if you are right. You decide to let x = 2. Substituting into 2x + 5x, you get 2(2) + 5(2) = 14. Substituting into your simplified expression you get 7(2) = 14. Since both expressions produced the same answer, you have direct confirmation that you have simplified correctly.
Example 1.1 E
Exercises
Mechanics
For questions 1–4, simplify the algebraic expressions.
1. 2a − 3a + 4 + 6a − 3
2. 5b(4b + 2)
3. ![]()
4. ![]()
5. Evaluate the power ![]()
6. Substitute the known variables and solve for the unknown variable:
I = Prt where P = $2,500, r = 0.06, and t = ![]()
Applications
For questions 7–11, simplify the algebraic expressions.
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. Evaluate the power: ![]()
For questions 13 and 14, substitute the known variables and solve for the unknown variable.
13. ![]() where FV = $3,417.24, i = 0.05, and N = 6
where FV = $3,417.24, i = 0.05, and N = 6
14. ![]() where FV = $10,000, N = 17, and i = 0.10
where FV = $10,000, N = 17, and i = 0.10
Challenge, Critical Thinking, & Other Applications
For questions 15–17, simplify the algebraic expressions.
![Rendered by QuickLaTeX.com {\left[ {\frac{{10{a^2}{b^3}{c^4}}}{{5{b^3}{c^4}}}} \right]^2} + 6{\left( {{a^8}} \right)^{{\raise0.7ex\hbox{](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-dc6c6e043db858722d0085e7b54be42d_l3.png) 1
1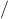 2
2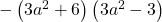
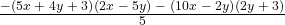
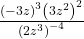
- Substitute the known variables and solve for the unknown variable.
![]()
where PMT = $500, i = 0.05, Δ% = 0.02, CY = 2, PY = 4, and N = 20
For questions 19-20, evaluate the expression.
1.2 Linear Equations: Manipulating and Solving
You are shopping at Old Navy for seven new outfits. The price points are $10 and $30. You really like the $30 outfits; however, your total budget can’t exceed $110. How do you spend $110 to acquire all the needed outfits without exceeding your budget while getting as many $30 items as possible?
This is a problem of linear equations, and it illustrates how you can use them to make an optimal decision. Let L represent the quantity of clothing at the low price point of $10, and H represent the quantity of clothing at the high price point of $30. This results in the following algebraic equations:
L + H = 7 (the total number of outfits you need)
$10L + $30H = $110 (your total budget)
By simultaneously solving these equations you can determine how many outfits at each price point you can purchase.
You will encounter many situations like this in your business career, for example, in making the best use of a manufacturer’s production capacity. Assume your company makes two products on the same production line and sells all its output. Each product contributes differently to your profitability, and each product takes a different amount of time to manufacture. What combination of each of these products should you make such that you operate your production line at capacity while also maximizing the profits earned? This section explores how to solve linear equations for unknown variables.
Understanding Equations
To manipulate algebraic equations and solve for unknown variables, you must first become familiar with some important language, including linear versus nonlinear equations and sides of the equation.
Parts of an Equation

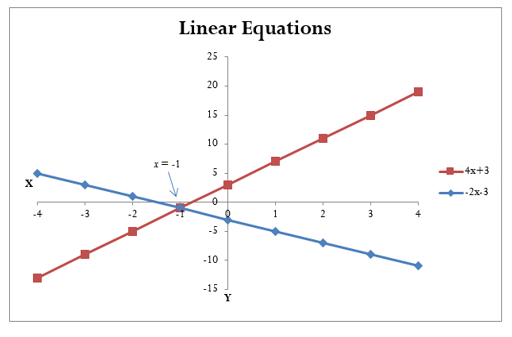
The goal in manipulating and solving a linear equation is to find a value for the unknown variable that makes the equation true. If you substitute a value of x = −1 into the above example, the left-hand side of the equation equals the right-hand side of the equation (see Figure 2.17). The value of x = −1 is known as the root, or solution, to the linear equation.
Solving One Linear Equation with One Unknown Variable
In your study of solving linear equations, you need to start by manipulating a single equation to solve for a single unknown variable. Later in this section you will extend from this foundation to the solution of two linear equations with two unknowns.
How It Works
To determine the root of a linear equation with only one unknown variable, apply the following steps:
Step 1: Your first goal is to separate the terms containing the literal coefficient from the terms that only have numerical coefficients. Collect all of the terms with literal coefficients on only one side of the equation and collect all of the terms with only numerical coefficients on the other side of the equation. It does not matter which terms go on which side of the equation, so long as you separate them.
To move a term from one side of an equation to another, take the mathematical opposite of the term being moved and add it to both sides. For example, if you want to move the +3 in 4x + 3 = −2x − 3 from the left-hand side to the right-hand side, the mathematical opposite of +3 is −3. When you move a term, remember the cardinal rule: What you do to one side of an equation you must also do to the other side of the equation. Breaking this rule breaks the equality in the equation.
Step 2: Combine all like terms on each side and simplify the equation according to the rules of algebra.
Step 3: In the term containing the literal coefficient, reduce the numerical coefficient to a 1 by dividing both sides of the equation by the numerical coefficient.
Important Notes
When you are unsure whether your calculated root is accurate, an easy way to verify your answer is to take the original equation and substitute your root in place of the variable. If you have the correct root, the left-hand side of the equation equals the right-hand side of the equation. If you have an incorrect root, the two sides will be unequal. The inequality typically results from one of the three most common errors in algebraic manipulation:
- The rules of BEDMAS have been broken.
- The rules of algebra have been violated.
- What was done to one side of the equation was not done to the other side of the equation.
Things To Watch Out For
When you move a term from one side of the equation to another using multiplication or division, remember that this affects each and every term on both sides of the equation. To remove the x from the denominator in the following equation, multiply both sides of the equation by x:
![]() becomes
becomes ![]() which then becomes
which then becomes ![]()
Multiplying every term on both sides by x maintains the equality.
Paths To Success
Negative numbers can cause some people a lot of grief. In moving terms from a particular side of the equation, many people prefer to avoid negative numerical coefficients in front of literal coefficients. Revisiting 4x + 3 = −2x − 3, you could move the 4x from the left side to the right side by subtracting 4x from both sides. However, on the right side this results in −6x. The negative is easily overlooked or accidentally dropped in future steps. Instead, move the variable to the left side of the equation, yielding a positive coefficient of 6x.
Example 1.2 A: How to Solve the Opening Example
Example 1.2 B: Solving a Linear Equation with One Unknown Variable
[table id=9 /]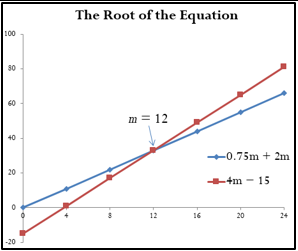
Example 1.2 C: Solving a Linear Equation with One Unknown Variable Containing Fractions
[table id=10 /]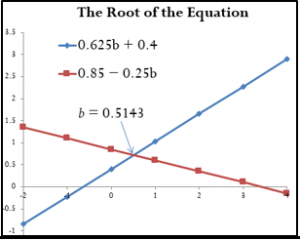
Solving Two Linear Equations with Two Unknown Variables
The manipulation process you have just practiced works well for solving one linear equation with one variable. But what happens if you need to solve two linear equations with two variables simultaneously? Remember when you were at Old Navy purchasing seven outfits earlier in this chapter (equation 1)? You needed to stay within a pricing budget (equation 2). Each equation had two unknown variables representing the number of lower-priced and higher-priced outfits.
The goal is to reduce two equations with two unknowns into a single linear equation with one unknown. Once this transformation is complete, you then identify the unknown variable by applying the three-step procedure for solving one linear equation, as just discussed.
When you work with two linear equations with two unknowns, the rules of algebra permit the following two manipulations:
- What you do to one side of the equation must be done to the other side of the equation to maintain the equality. Therefore, you can multiply or divide any equation by any number without changing the root of the equation. For example, if you multiply all terms of x + y = 2 by 2 on both sides, resulting in 2x + 2y = 4, the equality of the equation remains unchanged and the same roots exist.
- Terms that are on the same side of an equation can be added and subtracted between equations by combining like terms. Each of the two equations has a left side and right side. This rule permits taking the left side of the first equation and either adding or subtracting like terms on the left side of the second equation. When you perform this action, remember the first rule above. If you add the left sides of the equations together, you then must add the right side of both equations together to maintain equality.
How It Works
Follow these steps to solve two linear equations with two unknown variables:
Step 1: Write the two equations one above the other, vertically lining up terms that have the same literal coefficients and terms that have only the numerical coefficient. If necessary, the equations may need to be manipulated such that all of the literal coefficients are on one side with the numerical coefficients on the other side.
Step 2: Examine your two equations. Through multiplication or division, make the numerical coefficient on one of the terms containing a literal coefficient exactly equal to its counterpart in the other equation.
Step 3: Add or subtract the two equations as needed so as to eliminate the identical term from both equations.
Step 4: In the new equation, solve for the last literal coefficient.
Step 5: Substitute the root of the known literal coefficient into either of the two original equations. If one of the equations takes on a simpler structure, pick that equation.
Step 6: Solve your chosen equation for the other literal coefficient.
Paths To Success
Sometimes it is unclear exactly how you need to multiply or divide the equations to make two of the terms identical. For example, assume the following two equations:
4.9x + 1.5y = 38.3
2.7x − 8.6y = 17.8
If the goal is to make the terms containing the literal coefficient x identical, there are two alternative solutions:
- Take the larger numerical coefficient for x and divide it by the smaller numerical coefficient. The resulting number is the factor for multiplying the equation containing the smaller numerical coefficient. In this case, 4.9 ÷ 2.7 =
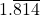 . Multiply all terms in the second equation by
. Multiply all terms in the second equation by 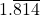 to make the numerical coefficients for x equal to each other, resulting in this pair of equations:
to make the numerical coefficients for x equal to each other, resulting in this pair of equations:
4.9x + 1.5y = 38.3
4.9x − ![]() y =
y = ![]() (every term multiplied by
(every term multiplied by ![]() )
)
- Take the first equation and multiply it by the numerical coefficient in the second equation. Then take the second equation and multiply it by the numerical coefficient in the first equation. In this case, multiply all terms in the first equation by 2.7. Then multiply all terms in the second equation by 4.9.
13.23x + 4.05y = 103.41 (every term multiplied by 2.7)
13.23x − 42.14y = 87.22 (every term multiplied by 4.9)
Note that both approaches successfully result in both equations having the same numerical coefficient in front of the literal coefficient x.
Ultimately, every pairing of linear equations with two unknowns can be converted into a single equation through substitution. To make the conversion, do the following:
- Solve either equation for one of the unknown variables.
- Take the resulting algebraic expression and substitute it into the other equation. This new equation is solvable for one of the unknown variables.
- Substitute your newfound variable into one of the original equations to determine the value for the other unknown variable.
Take the following two equations:
a + b = 4 2a + b = 6
- Solving the first equation for a results in a = 4 – b.
- Substituting the expression for a into the second equation and solving for b results in 2(4 – b) + b = 6, which solves as b = 2.
- Finally, substituting the root of b into the first equation to calculate a gives a + 2 = 4 resulting in a = 2. Therefore, the roots of these two equations are a = 2 and b = 2.
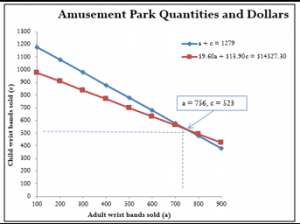
Example 1.2D: Buying Those Outfits
[table id=11 /]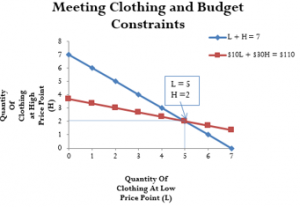
Paths To Success
One of the most difficult areas of mathematics involves translating words into mathematical symbols and operations. To assist in this translation, the table below lists some common language and the mathematical symbol that is typically associated with the word or phrase.
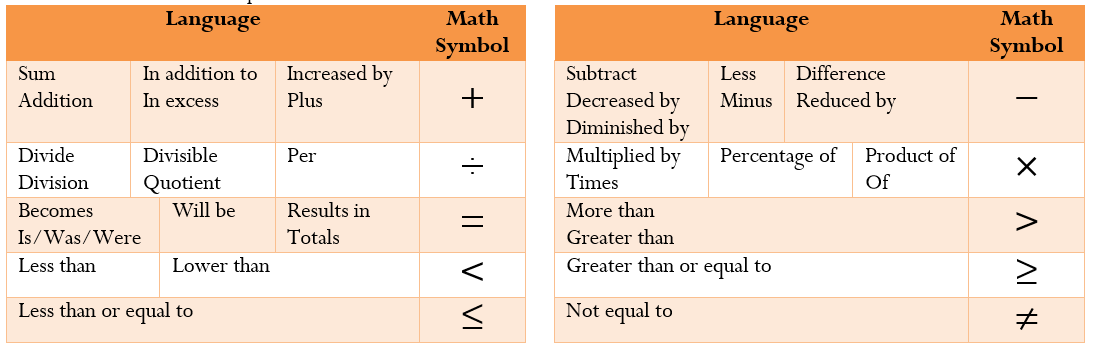
Example 1.2E: Solving Two Linear Equations with Two Unknowns
Exercises
Mechanics
Solve the following equations for the unknown variable.
1. 3(x − 5) = 15
2. 12b − 3 = 4 + 5b
3. 0.75(4m + 12) + 15 − 3(2m + 6) = 5(−3m + 1) + 25
Solve each of the following pairs of equations for both unknown variables.
4. x + y = 6
3x − 2y = 8
5. 4h − 7q = 13
6h + 3q = 33
6. ![]()
![]()
Applications
In questions 7 and 8, solve the equation for the unknown variable.
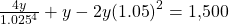
- $2,500(1 + 0.06t) + $1,000(1 + 0.04t) = $3,553.62
For exercises 9–14, read each question carefully and solve for the unknown variable(s).
- Pamela is cooking a roast for a 5:30 p.m. dinner tonight. She needs to set a delay timer on her oven. The roast takes 1 hour and 40 minutes to cook. The time right now is 2:20 p.m. How long of a delay must she set the oven for (before it automatically turns on and starts to cook the roast)?
- In 2010, 266 million North Americans were using the Internet, which represented a 146.3% increase in Internet users over the year 2000. How many North American Internet users were there in 2000?
- A human resource manager is trying to estimate the cost of a workforce accident. These costs usually consist of direct costs (such as medical bills, equipment damage, and legal expenses) and indirect costs (such as decreased output, production delays, and fines). From past experience, she knows that indirect costs average six times as much as direct costs. If she estimates the cost of an accident to be $21,000, what is the direct cost of the accident?
- In 2011, Canadian federal tax rates were 0% on the first $10,527 of gross income earned, 15% on the next $31,017, 22% on the next $41,544, 26% on the next $45,712, and 29% on anything more. If a taxpayer paid $28,925.35 in federal tax, what was her gross annual income for 2011?
- St. Boniface Hospital raises funds for research through its Mega Lottery program. In this program, 16,000 tickets are available for purchase at a price of one for $100 or three for $250. This year, the lottery sold out with sales of $1,506,050. To better plan next year’s lottery, the marketing manager wants to know how many tickets were purchased under each option this year.
- An accountant is trying to allocate production costs from two different products to their appropriate ledgers. Unfortunately, the production log sheet for last week has gone missing. However, from other documents he was able to figure out that 1,250 units in total were produced last week. The production machinery was run for 2,562.5 minutes, and he knows that Product A takes 1.5 minutes to manufacture while Product B takes 2.75 minutes to manufacture. How many units of each product were produced last week?
Challenge, Critical Thinking, & Other Applications
- Jacob owns 15,000 shares in a corporation, which represents 2% of all issued shares for the company. He sold of his shares to another investor for $7,800. What is the total value for all of the shares issued by the company?
- Two cellphone companies are offering different rate plans. Rogers is offering $19.99 per month, which includes a maximum of 200 weekday minutes plus $0.35 for every minute above the maximum. TELUS is offering $39.99 for a maximum 300 weekday minutes, but it charges $0.10 for every minute above the maximum. Above how many minutes would TELUS be the better choice?
- Marianne, William, Hendrick, and Charlotte have all decided to go into business together. They need $175,000 in initial capital funding. William was able to contribute 20% less than Marianne, Hendrick contributed 62.5% more than William, and Charlotte contributed $5,000 less than half as much as Marianne. How much did each partner contribute to the initial funds?
- A mall is being constructed and needs to meet the legal requirements for parking availability. Parking laws require one parking stall for every 100 square feet of retail space. The mall is designed to have 1,200,000 square feet of retail space. Of the total parking stalls available, 2% need to be handicap accessible, there need to be three times as many small car spaces as handicap spaces, RV spaces need to be one-quarter of the number of small car spaces, and the rest of the spaces are for regular stalls. How many of each type of parking space does the mall require?
- Simplify the following equation into the format of #z = # and find the root. Verify the solution through substitution.
![]()
- Find the roots for the following pairs of equations. Verify the solution through substitution into both equations.
![]()
![]()
1.3 Natural Logarithms
Your investment is earning compound interest of 6% per year. You wonder how long it will take to double in value. Answering this question requires you to solve an equation in which the unknown variable is located in the exponent instead of the base position. To find the answer, you need logarithms, which are reviewed in this section and will be applied in Chapters 9 and 11.
Logarithms
A logarithm is defined as the exponent to which a base must be raised to produce a particular power. Although the base can assume any value, two values for the base are most often used.
- A Base Value of 10. This is referred to as a common logarithm. Thus, if you have 102 = 100, then 2 is the common logarithm of 100 and this is written as log10(100) = 2, or just log(100) = 2 (you can assume the 10 if the base is not written). The format for a common logarithm can then be summarized as
log(power) = exponent
If you have 10x = y, then log(y) = x.
- A Base Value of e. This is referred to as a natural logarithm. In mathematics, there is a known constant e, which is a nonterminating decimal and has an approximate value of e = 2.71828182845. If you have e3 = 20.085537, then 3 is the natural logarithm of 20.085537 and you write this as ln(20.085537) = 3. The format for a natural logarithm is then summarized as:
ln(power) = exponent
If you have e4 = 54.59815, then ln(54.59815) = 4
Common logarithms have been used in the past when calculators were not equipped with power functions. However, with the advent of computers and advanced calculators that have power functions, the natural logarithm is now the most commonly used format. From here on, this textbook focuses on natural logarithms only.
Properties of Natural Logarithms
Natural logarithms possess six properties:
- The natural logarithm of 1 is zero. For example, if 1 is the power and 0 is the exponent, then you have e0 = 1. This obeys the laws of exponents discussed in Section 2.4 of this chapter.
- The natural logarithm of any number greater than 1 is a positive number. For example, the natural logarithm of 2 is 0.693147, or e0.693147 = 2.
- The natural logarithm of any number less than 1 is a negative number. For example, the natural logarithm of 0.5 is −0.693147, or e−0.693147 = 0.5. Similar to property 1, this obeys the laws of exponents discussed in Section 2.4, where e−0.693147 =
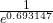 , always producing a proper fraction.
, always producing a proper fraction. - A natural logarithm cannot be less than or equal to zero. Since e is a positive number with an exponent, there is no value of the exponent that can produce a power of zero. As well, it is impossible to produce a negative number when the base is positive.
- The natural logarithm of the quotient of two positive numbers is
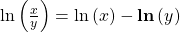 . For example,
. For example, 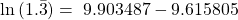 or
or 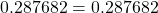
- The natural logarithm of a power of a positive base is . This property allows you to relocate the exponent down into the base. . Demonstrating this principle,
![]() %
%
ln(1.056) = 6 × ln(1.05)
ln(1.340095) = 6 × 0.048790
0.292741= 0.292741
Important Notes
Applying natural logarithms on your TI BAII Plus calculator requires two steps.
- Input the power.
- With the power still on the display, press the LN key located in the left-hand column of your keypad. The solution on the display is the value of the exponent. If you key in an impossible value for the natural logarithm, an “Error 2” message is displayed on the screen.
If you know the exponent and want to find out the power, remember that ex = power. This is called the anti-log function. Thus, if you know the exponent is 2, then e2 = 7.389056. On your calculator, the anti-log can be located on the second shelf directly above the LN button. To access this function, key in the exponent first and then press 2nd ex.
Paths To Success
You do not have to memorize the mathematical constant value of e. If you need to recall this value, use an exponent of 1 and access the ex function. Hence, e1 = 2.71828182845.
Give It Some Thought
For each of the following powers, determine if the natural logarithm is positive, negative, zero, or impossible.
a. 2.3 b. 1 c. 0.45 d. 0.97 e. −2 f. 4.83 g. 0
Solutions:
- a. positive (property 2) b. zero (Property 1) c. negative (property 3)
- negative (property 3) e. impossible (Property 4) f. positive (property 2)
- impossible (property 4)
Example 1.3 A: Applying Natural Logarithms and Properties
[table id=13 /]
Exercises
Mechanics
Using your financial calculator, evaluate each of the following. Write your answer using the ex = power format. Round your answers to six decimals.
2. ln(0.7445)
3. ln(1.83921)
4. ln(13.2746)
5. ln(0.128555)
Applications
For each of the following, demonstrate the fifth property of natural logarithms, where ![]() .
.
6. ln[(1.02)23]
7. ln[(1.01275)41]
8. ln[(1.046)34]
Using ![]() , substitute the known values and evaluate the expression.
, substitute the known values and evaluate the expression.
| FV | PV | i | |
| 12. | $78,230 | $25,422 | 0.0225 |
| 13. | $233,120 | $91,450 | 0.0425 |
| 14. | $18,974 | $8,495 | 0.02175 |
Challenge, Critical Thinking, & Other Applications
Using FV = PV(1 + i)N, substitute in the known values and solve for N.
| FV | PV | i | |
| 15. | $18,302.77 | $14,000.00 | 0.015 |
| 16. | $58,870.20 | $36,880 | 0.01 |
The Language of Business Mathematics
algebraic equation An equation that takes two algebraic expressions and makes them equal to each other.
algebraic expression Indicates the relationship between and mathematical operations that must be conducted on a series of numbers or variables.
base The entire amount or quantity of concern.
BEDMAS An order of operations acronym standing for Brackets, Exponents, Division, Multiplication, Addition, and Subtraction.
common logarithm A logarithm with a base value of 10.
complex fraction A fraction that has fractions within fractions, combining elements of compound, proper, and/or improper fractions together.
compound fraction A fraction that combines an integer with either a proper or improper fraction.
denominator Any term by which some other term is divided; commonly the number on the bottom of a fraction.
divisor line The line that separates the numerator and the denominator in a fraction.
equivalent fractions Two or more fractions of any type that have the same numerical value upon completion of the division.
exponent A mathematical shorthand notation that indicates how many times a quantity is multiplied by itself
factor Components of terms that are separated from by multiplication or division signs.
fraction A part of a whole.
improper fraction A fraction in which the numerator is larger than the denominator.
left side of the equation The part of an equation that is to the left of the equal sign.
like terms Terms that have the same literal coefficient.
linear equation An algebraic expression in which the variable has an exponent of 1; when plotted, it will form a straight line.
literal coefficient A factor that is a variable.
logarithm The exponent to which a base must be raised to produce a particular power.
monomial An algebraic expression with only one term.
natural logarithm A logarithm with a base value of the mathematical constant e.
nomial The number of terms that appear in an algebraic expression.
nonlinear equation An algebraic expression in which the variable has an exponent other than 1; when plotted, it will not form a straight line.
numerator Any term into which some other term is being divided; commonly the number on the top in a fraction.
numerical coefficient A factor that is numerical.
percentage A part of a whole expressed in hundredths.
polynomial An algebraic expression with two or more terms.
portion Represents part of a whole or base.
proper fraction A fraction in which the numerator is smaller than the denominator.
rate Expresses a relationship between a portion and a base.
right side of the equation The part of an equation that is to the right of the equal sign.
root The value of the unknown variable that will make a linear equation true.
substitution Replacing the literal coefficients of an algebraic expression with their numerical values.
term In any algebraic expression, the components that are separated by addition and subtraction.
triangle technique A memorization technique that displays simple multiplication formulae in the form of a triangle. Anything on the same line is multiplied, and items above or below each other are divided to arrive at various solutions.
Chapter 1: Review of the Basics (Answers to textbook questions)
-
1.1 Algebraic Expressions
- 5a+1
- 20b2 +10b
- 2x2+4x+4.5
- (1+i)17
- 4
- I = $55.48
- 15r2 +3r+5
- 1,024x40
- 0.75t+3.5t3
- 2 + 3(1+i)3 -5(1+i)6
- 3.995628R
- 0.0256
- PV=$2,550
- PMT= $246.64
- a4 -9a2 +18
- -2x2 -0.6xy+4.8y2 -7.2x+4.2y
- -3,888z19
- $15,223.10
- $39,963.05
- $12,466.44
-
1.2 Linear Equation
- x=10
- b=1
- m=2
- x=4, y=2
- h=5, q=1
- a=8, b=0.6
- y= $620.14
- t=6.1513̅
- Delay = 1.5 hours
- 10.Users in 2000 = 107,998,376
- Direct cost = $3,000
- Gross income = $140,000
- Single tickets = 10,363; 3-pack Tickets = 1,879
- A = 700 units; B = 550 units
- Company shares = $975,000
- 240 minutes
- Marianne = $50,000; William = $40,000; Hendrick = $65,000; Charlotte = $20,000
- Regular stalls = 10,860; Handicap stalls = 240; Small car stalls = 720; RV stalls = 180
- Z = $25,000
- q = 2.78; r = 9.31
-
1.3 Natural Logarithms
- e1.367188 = 3.9243
- e-0.295042 = 0.7445
- e0.609336 = 1.83921
- e2.585852 =12.2746
- e-2.051398 = 0.128555
- 0.392393
- 2.302585
- 1.811554
- 0.455460
- 0.519446
- 1.529094
- 50.517191
- 22.48254
- 36.904108
- N=87.808096
- N=160.423164
- 0.583198
- 1.451535
- 403.428793
- 33.115452

