11 Finance
Chapter 11 Topics
11.1 Simple and Compound Interest
11.2 Annuities
11.3 Payout Annuities
Section 11.1 Simple and Compound Interest
Discussing interest starts with the principal, or amount your account starts with. This could be a starting investment, or the starting amount of a loan. Interest, in its most simple form, is calculated as a percent of the principal. For example, if you borrowed $100 from a friend and agree to repay it with 5% interest, then the amount of interest you would pay would just be 5% of 100: $100(0.05) = $5. The total amount you would repay would be $105, the original principal plus the interest.
Simple One-time Interest
![]()
![]()
I is the interest
A is the end amount: principal plus interest
P is the principal (starting amount)
r is the interest rate in decimal form. Example: 5% = 0.05
Example 1
A friend asks to borrow $300 and agrees to repay it in 30 days with 3% interest. How much interest will you earn?
P = $300 the principal
r = 0.03 3% rate
I = $300(0.03) = $9. You will earn $9 interest.
One-time simple interest is only common for extremely short-term loans. For longer term loans, it is common for interest to be paid on a daily, monthly, quarterly, or annual basis. In that case, interest would be earned regularly. For example, bonds are essentially a loan made to the bond issuer (a company or government) by you, the bond holder. In return for the loan, the issuer agrees to pay interest, often annually. Bonds have a maturity date, at which time the issuer pays back the original bond value.
Example 2
Suppose your city is building a new park, and issues bonds to raise the money to build it. You obtain a $1,000 bond that pays 5% interest annually that matures in 5 years. How much interest will you earn?
Each year, you would earn 5% interest: $1000(0.05) = $50 in interest. So over the course of five years, you would earn a total of $250 in interest. When the bond matures, you would receive back the $1,000 you originally paid, leaving you with a total of $1,250.
We can generalize this idea of simple interest over time.
Simple Interest over Time
![]()
![]()
I is the interest
A is the end amount: principal plus interest
P is the principal (starting amount)
r is the interest rate in decimal form
t is time
The units of measurement (years, months, etc.) for the time should match the time period for the interest rate.
APR – Annual Percentage Rate
Interest rates are usually given as an annual percentage rate (APR) – the total interest that will be paid in the year. If the interest is paid in smaller time increments, the APR will be divided up.
For example, a 6% APR paid monthly would be divided into twelve 0.5% payments.
A 4% annual rate paid quarterly would be divided into four 1% payments.
Example 3
Treasury Notes (T-notes) are bonds issued by the federal government to cover its expenses. Suppose you obtain a $1,000 T-note with a 4% annual rate, paid semi-annually, with a maturity in 4 years. How much interest will you earn?
Since interest is being paid semi-annually (twice a year), the 4% interest will be divided into two 2% payments.
P = $1000 the principal
r = 0.02 2% rate per half-year
t = 8 4 years = 8 half-years
I = $1000(0.02)(8) = $160. You will earn $160 interest total over the four years.
Try it Now
1. A loan company charges $30 interest for a one month loan of $500. Find the annual interest rate they are charging.
Compound Interest
With simple interest, we were assuming that we pocketed the interest when we received it. In a standard bank account, any interest we earn is automatically added to our balance, and we earn interest on that interest in future years. This reinvestment of interest is called compounding. We looked at this situation earlier, in the chapter on exponential growth.
Compound Interest
![]()
A is the balance in the account after t years.
P is the starting balance of the account (also called initial deposit, or principal)
r is the annual interest rate in decimal form
k is the number of compounding periods in one year.
If the compounding is done annually (once a year), k = 1.
If the compounding is done quarterly, k = 4.
If the compounding is done monthly, k = 12.
If the compounding is done daily, k = 365.
The most important thing to remember about using this formula is that it assumes that we put money in the account once and let it sit there earning interest.
Example 4
A certificate of deposit (CD) is a savings instrument that many banks offer. It usually gives a higher interest rate, but you cannot access your investment for a specified length of time. Suppose you deposit $3000 in a CD paying 6% interest, compounded monthly. How much will you have in the account after 20 years?
In this example,
P = $3000 the initial deposit
r = 0.06 6% annual rate
k = 12 12 months in 1 year
t = 20 since we’re looking for how much we’ll have after 20 years
So
![]()
(round your answer to the nearest penny)
Let us compare the amount of money earned from compounding against the amount you would earn from simple interest
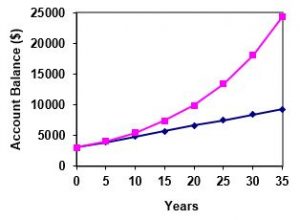
|
Years |
Simple Interest ($15 per month) |
6% compounded monthly = 0.5% each month. |
|
5 |
$3900 |
$4046.55 |
|
10 |
$4800 |
$5458.19 |
|
15 |
$5700 |
$7362.28 |
|
20 |
$6600 |
$9930.61 |
|
25 |
$7500 |
$13394.91 |
|
30 |
$8400 |
$18067.73 |
|
35 |
$9300 |
$24370.65 |
As you can see, over a long period of time, compounding makes a large difference in the account balance. You may recognize this as the difference between linear growth and exponential growth.
Evaluating exponents on the calculator
When we need to calculate something like 53 it is easy enough to just multiply 5⋅5⋅5=125. But when we need to calculate something like 1.005240 , it would be very tedious to calculate this by multiplying 1.005 by itself 240 times! So to make things easier, we can harness the power of our calculators.
Most scientific calculators have a button for exponents. It is typically either labeled like:
^ , yx, or xy.
To evaluate 1.005240 we’d typ
e 1.005 ^ 240, or 1.005 yx 240. Try it out – you should get something around 3.3102044758.
Example 5
You know that you will need $40,000 for your child’s education in 18 years. If your account earns 4% compounded quarterly, how much would you need to deposit now to reach your goal?
In this example,
We’re looking for P.
r = 0.04 4%
k = 4 4 quarters in 1 year
t = 18 Since we know the balance in 18 years
A = $40,000 The amount we have in 18 years
In this case, we’re going to have to set up the equation, and solve for P.
![Rendered by QuickLaTeX.com \[\begin{array}{l} 40000 = P{\left( {1 + \frac{{0.04}}{4}} \right)^{18 \times 4}}\\ 40000 = P(2.0471)\\ P = \frac{{40000}}{{2.0471}} = \$ 19539.84 </div> \end{array}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-66eeaaf45e9537881e9eecbc70fe989f_l3.png)
So you would need to deposit $19,539.84 now to have $40,000 in 18 years.
Rounding
It is important to be very careful about rounding when calculating things with exponents. In general, you want to keep as many decimals during calculations as you can. Be sure to keep at least 3 significant digits (numbers after any leading zeros). Rounding 0.00012345 to 0.000123 will usually give you a “close enough” answer, but keeping more digits is always better. If your calculator allows it, do all your calculations without rounding in the calculator and only round the final answer.
Example 6
To see why not over-rounding is so important, suppose you were investing $1000 at 5% interest compounded monthly for 30 years.
P = $1000 the initial deposit
r = 0.05 5%
k = 12 12 months in 1 year
t = 30 since we’re looking for the amount after 30 years
If we first compute r/k, we find 0.05/12 = 0.00416666666667
Here is the effect of rounding this to different values:
| Gives A to be: | Error | |
| 0.004 | $4208.59 | $259.15 |
| 0.0042 | $ 4521.45 | $53.71 |
| 0.00417 | $ 4473.09 | $5.35 |
| 0.004167 | $ 4468.28 | $0.54 |
| 0.0041667 | $ 4467.80 | $0.06 |
| no rounding | $ 4467.74 |
If you’re working in a bank, of course you wouldn’t round at all. For our purposes, the answer we got by rounding to 0.00417, three significant digits, is close enough – $5 off of $4500 isn’t too bad. Certainly keeping that fourth decimal place wouldn’t have hurt.
Using your calculator
In many cases, you can avoid rounding completely by how you enter things in your calculator. For example, in the example above, we needed to calculate ![]()
We can quickly calculate 12×30 = 360, giving ![]() .
.
Now we can use the calculator.
| Type this | Calculator Shows |
| 0.05 ÷ 12 = | 0.00416666666667 |
| + 1 = | 1.00416666666667 |
| yx 360 = | 4.46774431400613 |
| × 1000 = | 4467.74431400613 |
The previous steps were assuming you have a “one operation at a time” calculator; a more advanced calculator will often allow you to type in the entire expression to be evaluated. If you have a calculator like this, you will probably just need to enter:
1000 × ( 1 + 0.05 ÷ 12 ) yx 360 = .
Or
1000 × ( 1 + 0.05 ÷ 12 ) ^ 360 = .
Try it Now
2. If $70,000 are invested at 7% compounded monthly for 25 years, find the end balance.
Because of compounding throughout the year, with compound interest the actual increase in a year is more than the annual percentage rate. If $1,000 were invested at 10%, the table below shows the value after 1 year at different compounding frequencies:
|
Frequency |
Value after 1 year |
|
Annually |
$1100 |
|
Semiannually |
$1102.50 |
|
Quarterly |
$1103.81 |
|
Monthly |
$1104.71 |
|
Daily |
$1105.16 |
If we were to compute the actual percentage increase for the daily compounding, there was an increase of ![]() 1,000, for a percentage increase of
1,000, for a percentage increase of ![]() = 10.516% increase. This quantity is called the annual percentage yield (APY).
= 10.516% increase. This quantity is called the annual percentage yield (APY).
Notice that given any starting amount, the amount after 1 year would be
![]() . To find the total change, we would subtract the original amount, then to find the percentage change we would divide that by the original amount:
. To find the total change, we would subtract the original amount, then to find the percentage change we would divide that by the original amount:
![]()
Annual Percentage Yield
The annual percentage yield is the actual percent a quantity increases in one year. It can be calculated as
![]()
Notice this is equivalent to finding the value of $1 after 1 year, and subtracting the original dollar.
Example 7
Bank A offers an account paying 1.2% compounded quarterly. Bank B offers an account paying 1.1% compounded monthly. Which is offering a better rate?
We can compare these rates using the annual percentage yield – the actual percent increase in a year.
Bank A: ![]() = 1.2054%
= 1.2054%
Bank B: ![]() = 1.1056%
= 1.1056%
Bank B’s monthly compounding is not enough to catch up with Bank A’s better APR. Bank A offers a better rate.
Example 8
If you invest $2000 at 6% compounded monthly, how long will it take the account to double in value?
This is a compound interest problem, since we are depositing money once and allowing it to grow. In this problem,
P = $2000 the initial deposit
r = 0.06 6% annual rate
k = 12 12 months in 1 year
So our general equation is
![]()
. We also know that we want our ending amount to be double of $2000, which is $4000, so we’re looking for t so that A = 4000. To solve this, we set our equation for A equal to 4000.
![]()
Divide both sides by 2000
![]()
To solve for the exponent, take the log of both sides
![]()
Use the exponent property of logs on the right side
![]()
Now we can divide both sides by 12log(1.005)
![]()
Approximating this to a decimal
t = 11.581
It will take about 11.581 years for the account to double in value. Note that your answer may come out slightly differently if you had evaluated the logs to decimals and rounded during your calculations, but your answer should be close. For example if you rounded log(2) to 0.301 and log(1.005) to 0.00217, then your final answer would have been about 11.577 years.
Try it Now Answers
1.
I = $30 of interest
P = $500 principal
r = unknown
t = 1 month
Using I = Prt, we get 30 = 500·r·1. Solving, we get r = 0.06, or 6%. Since the time was monthly, this is the monthly interest. The annual rate would be 12 times this: 72% interest.
2.
![]()
Section 11.2 Annuities
For most of us, we aren’t able to put a large sum of money in the bank today. Instead, we save for the future by depositing a smaller amount of money from each paycheck into the bank. This idea is called a savings annuity. Most retirement plans like 401k plans or IRA plans are examples of savings annuities.
Suppose we will deposit $100 each month into an account paying 6% interest. How much will we have after a year? We assume that the account is compounded with the same frequency as we make deposits unless stated otherwise. In this example:
r = 0.06 (6%)
k = 12 (12 compounds/deposits per year)
d = $100 (our deposit per month)
t = 1 year
With ordinary annuities we assume the payment is made at the end of the period. The $100 we deposit at the end of the first month will earn interest for 11 months and at the end of the year will be worth.
![]()
The $100 deposited at the end of the second month will have 10 months to grow, and will be worth
![]()
at the end of the year. This pattern continues down to the last deposit, which has no time to compound, and will be worth A = 100.
In total, we will have accumulated:
![]()
This equation leaves a lot to be desired, though – it doesn’t make calculating the ending balance any easier! To simplify things, multiply both sides of the equation by 1.005:
![]()
Distributing on the right side of the equation gives
![]()
Now we’ll line this up with like terms from our original equation, and subtract each side
![]()
Almost all the terms cancel on the right hand side when we subtract, leaving
![]()
Now we solve this equation for A.
![Rendered by QuickLaTeX.com \[\begin{array}{l} 0.005A = 100\left( {{{\left( {1.005} \right)}^{12}} - 1} \right)\\ A = \frac{{100\left( {{{\left( {1.005} \right)}^{12}} - 1} \right)}}{{0.005}} \end{array}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-98f192c90d90441d0780951fd0987534_l3.png)
Recall 0.005 was r/k, 100 was the deposit d, and 12 was the number of months, kt. Generalizing this result, we get the saving annuity formula.
Annuity Formula
![]()
A is the balance in the account after t years.
d is the regular deposit (the amount you deposit each year, each month, etc.)
r is the annual interest rate in decimal form.
k is the number of compounding periods in one year.
If the compounding frequency is not explicitly stated, assume there are the same number of compounds in a year as there are deposits made in a year.
For example, if the compounding frequency isn’t stated:
If you make your deposits every month, use monthly compounding, k = 12.
If you make your deposits every year, use yearly compounding, k = 1.
If you make your deposits every quarter, use quarterly compounding, k = 4.
Etc.
When do you use this
Annuities assume that you put money in the account on a regular schedule (every month, year, quarter, etc.) and let it sit there earning interest.
Compound interest assumes that you put money in the account once and let it sit there earning interest.
Compound interest: One deposit
Annuity: Many deposits.
Example 1
A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100 each month into an IRA earning 6% interest, how much will you have in the account after 20 years?
In this example,
d = $100 the monthly deposit
r = 0.06 6% annual rate
k = 12 since we’re doing monthly deposits, we’ll compound monthly
t = 20 we want the amount after 20 years
Putting this into the equation:
![Rendered by QuickLaTeX.com \[\begin{array}{l} A = \frac{{100\left( {{{\left( {1 + \frac{{0.06}}{{12}}} \right)}^{20(12)}} - 1} \right)}}{{\left( {\frac{{0.06}}{{12}}} \right)}}\\ A = \frac{{100\left( {{{\left( {1.005} \right)}^{240}} - 1} \right)}}{{\left( {0.005} \right)}}\\ A = \frac{{100\left( {3.310 - 1} \right)}}{{\left( {0.005} \right)}}\\ A = \frac{{100\left( {2.310} \right)}}{{\left( {0.005} \right)}} = \$ 46200 </div> \end{array}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-5c484363b0bee075a333ea7cfef744a9_l3.png)
The account will grow to $46,200 after 20 years.
Notice that you deposited into the account a total of $24,000 ($100 a month for 240 months). The difference between what you end up with and how much you put in is the interest earned. In this case it is $46,200 – $24,000 = $22,200.
Example 2
You want to have $200,000 in your account when you retire in 30 years. Your retirement account earns 8% interest. How much do you need to deposit each month to meet your retirement goal?
In this example,
We’re looking for d.
r = 0.08 8% annual rate
k = 12 since we’re depositing monthly
t = 30 30 years
A = $200,000 The amount we want to have in 30 years
In this case, we’re going to have to set up the equation, and solve for d.
![Rendered by QuickLaTeX.com \[\begin{array}{l} 200,000 = \frac{{d\left( {{{\left( {1 + \frac{{0.08}}{{12}}} \right)}^{30(12)}} - 1} \right)}}{{\left( {\frac{{0.08}}{{12}}} \right)}}\\ 200,000 = \frac{{d\left( {{{\left( {1.00667} \right)}^{360}} - 1} \right)}}{{\left( {0.00667} \right)}}\\ 200,000 = d(1491.57)\\ d = \frac{{200,000}}{{1491.57}} = \$ 134.09 </div> \end{array}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-2a9ff41844e531bcf91cef47c68157b9_l3.png)
So you would need to deposit $134.09 each month to have $200,000 in 30 years if your account earns 8% interest
Try it Now
1. A more conservative investment account pays 3% interest. If you deposit $5 a day into this account, how much will you have after 10 years? How much is from interest?
Example 3
If you invest $100 each month into an account earning 3% compounded monthly, how long will it take the account to grow to $10,000?
This is a savings annuity problem since we are making regular deposits into the account.
d = $100 the monthly deposit
r = 0.03 3% annual rate
k = 12 since we’re doing monthly deposits, we’ll compound monthly
We don’t know t, but we want A to be $10,000.
Putting this into the equation:
![Rendered by QuickLaTeX.com \[10,000 = \frac{{100\left( {{{\left( {1 + \frac{{0.03}}{{12}}} \right)}^{12t}} - 1} \right)}}{{\left( {\frac{{0.03}}{{12}}} \right)}}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-3b2852c9f0a3c2c78d8862224675c601_l3.png)
Simplifying the fractions a bit
![Rendered by QuickLaTeX.com \[10,000 = \frac{{100\left( {{{\left( {1.0025} \right)}^{12t}} - 1} \right)}}{{0.0025}}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-aebeca94e505610271e206230e500750_l3.png)
We want to isolate the exponential term, 1.002512t, so multiply both sides by 0.0025
![]()
Divide both sides by 100
![]()
Add 1 to both sides
![]()
Now take the log of both sides
![]()
Use the exponent property of logs
![]()
Divide by 12log(1.0025)
![]()
Approximating to a decimal
t = 7.447 years
It will take about 7.447 years to grow the account to $10,000.
Try it Now Answers
1.
d = $5 the daily deposit
r = 0.03 3% annual rate
k = 365 since we’re doing daily deposits, we’ll compound daily
t = 10 we want the amount after 10 years
![]()
$21,282.07
We would have deposited a total of $5·365·10 = $18,250, so $3,032.07 is from interest
Section 11.3 Payout Annuities
In the last section you learned about annuities. In an annuity, you start with nothing, put money into an account on a regular basis, and end up with money in your account.
In this section, we will learn about a variation called a Payout Annuity. With a payout annuity, you start with money in the account, and pull money out of the account on a regular basis. Any remaining money in the account earns interest. After a fixed amount of time, the account will end up empty.
Payout annuities are typically used after retirement. Perhaps you have saved $500,000 for retirement, and want to take money out of the account each month to live on. You want the money to last you 20 years. This is a payout annuity. The formula is derived in a similar way as we did for savings annuities. The details are omitted here.
Payout Annuity Formula
![]()
P is the balance in the account at the beginning (starting amount, or principal).
w is the regular withdrawal (the amount you take out each year, each month, etc.)
r is the annual interest rate (in decimal form. Example: 5% = 0.05)
k is the number of compounding periods in one year.
t is the number of years we plan to take withdrawals
Like with annuities, the compounding frequency is not always explicitly given, but is determined by how often you take the withdrawals.
When do you use this
Payout annuities assume that you take money from the account on a regular schedule (every month, year, quarter, etc.) and let the rest sit there earning interest.
Compound interest: One deposit
Annuity: Many deposits.
Payout Annuity: Many withdrawals
Example 1
After retiring, you want to be able to take $1000 every month for a total of 20 years from your retirement account. The account earns 6% interest. How much will you need in your account when you retire?
In this example,
w = $1000 the monthly withdrawal
r = 0.06 6% annual rate
k = 12 since we’re doing monthly withdrawals, we’ll compound monthly
t = 20 since were taking withdrawals for 20 years
We’re looking for P; how much money needs to be in the account at the beginning.
Putting this into the equation:
![Rendered by QuickLaTeX.com \[\begin{array}{l} P = \frac{{1000\left( {1 - {{\left( {1 + \frac{{0.06}}{{12}}} \right)}^{ - 20(12)}}} \right)}}{{\left( {\frac{{0.06}}{{12}}} \right)}}\\ P = \frac{{1000 \times \left( {1 - {{\left( {1.005} \right)}^{ - 240}}} \right)}}{{\left( {0.005} \right)}}\\ P = \frac{{1000 \times \left( {1 - 0.302} \right)}}{{\left( {0.005} \right)}} = \$ 139,600 </div> \end{array}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-ba4269cc3dd1e6e4bcd3873a4958d2d3_l3.png)
You will need to have $139,600 in your account when you retire.
Notice that you withdrew a total of $240,000 ($1000 a month for 240 months). The difference between what you pulled out and what you started with is the interest earned. In this case it is $240,000 – $139,600 = $100,400 in interest.
Evaluating negative exponents on your calculator
With these problems, you need to raise numbers to negative powers. Most calculators have a separate button for negating a number that is different than the subtraction button. Some calculators label this (-) , some with +/- . The button is often near the = key or the decimal point.
If your calculator displays operations on it (typically a calculator with multiline display), to calculate 1.005-240 you’d type something like: 1.005 ^ (-) 240
If your calculator only shows one value at a time, then usually you hit the (-) key after a number to negate it, so you’d hit: 1.005 yx 240 (-) =
Give it a try – you should get 1.005-240 = 0.302096
Example 2
You know you will have $500,000 in your account when you retire. You want to be able to take monthly withdrawals from the account for a total of 30 years. Your retirement account earns 8% interest. How much will you be able to withdraw each month?
In this example,
We’re looking for w.
r = 0.08 8% annual rate
k = 12 since we’re withdrawing monthly
t = 30 30 years
P = $500,000 we are beginning with $500,000
In this case, we’re going to have to set up the equation, and solve for w.
![Rendered by QuickLaTeX.com \[\begin{array}{l} 500,000 = \frac{{w\left( {1 - {{\left( {1 + \frac{{0.08}}{{12}}} \right)}^{ - 30(12)}}} \right)}}{{\left( {\frac{{0.08}}{{12}}} \right)}}\\ 500,000 = \frac{{w\left( {1 - {{\left( {1.00667} \right)}^{ - 360}}} \right)}}{{\left( {0.00667} \right)}}\\ 500,000 = w(136.232)\\ w = \frac{{500,000}}{{136.232}} = \$ 3670.21 </div> \end{array}\]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-3e272039bac180cf52cad1812698b534_l3.png)
You would be able to withdraw $3,670.21 each month for 30 years.
Try it Now
1. A donor gives $100,000 to a university, and specifies that it is to be used to give annual scholarships for the next 20 years. If the university can earn 4% interest, how much can they give in scholarships each year?
Try it Now Answers
1.
w = unknown
r = 0.04 4% annual rate
k = 1 since we’re doing annual scholarships
t = 20 20 years
P = 100,000 we’re starting with $100,000
Solving for w gives $7,358.18 each year that they can give in scholarships.
It is worth noting that usually donors instead specify that only interest is to be used for scholarship, which makes the original donation last indefinitely. If this donor had specified that, $100,000(0.04) = $4,000 a year would have been available.

