3.3 Markdown: Setting the Sale Price

Everybody Loves a Sale

Flashy signs in a retail store announce, “40% off, today only!” Excitedly you purchase three tax-free products with regular price tags reading $100, $250, and $150. The cashier processing the transaction informs you that your total is $325. You are about to hand over your credit card when something about the total makes you pause. The regular total of all your items is $500. If they are 40% off, you should receive a $200 deduction and pay only $300. The cashier apologizes for the mistake and corrects your total.

Although most retail stores use automated checkout systems, these systems are ultimately programmed by human beings. A computer system is only as accurate as the person keying in the data. A study by the Competition Bureau revealed that 6.3% of items at various retail stores scanned incorrectly. The average error spread is up to 13% around the actual product’s price![1] Clearly, it is important for you as a consumer to be able to calculate markdowns.

Businesses must also thoroughly understand markdowns so that customers are charged accurately for their purchases. Businesses must always comply with the Competition Act of Canada, which specifically defines legal pricing practices. If your business violates this law, it faces severe penalties.

The Importance of Markdowns

A markdown is a reduction from the regular selling price of a product resulting in a lower price. This lower price is called the sale price to distinguish it from the selling price.

Many people perceive markdowns as a sign of bad business management decisions. However, in most situations this is not true. Companies must always attempt to forecast the future. In order to stock products, a reseller must estimate the number of units that might sell in the near future for every product that it carries. This is both an art and a science. While businesses use statistical techniques that predict future sales with a relative degree of accuracy, consumers are fickle and regularly change shopping habits. Markdowns most commonly occur under four circumstances:

Clearing Out Excess or Unwanted Inventory

In these situations, the business thought it could sell 100 units; however, consumers purchased only 20 units. In the case of seasonal inventory, such as Christmas items on Boxing Day, the retailer wishes to avoid packing up and storing the inventory until the next season.

Clearing Out Damaged or Discontinued Items

Selling a damaged product at a discount is better than not selling it at all. When products are discontinued, this leaves shelf space underused, so it is better to clear the item out altogether to make room for profitable items that can keep the shelves fully stocked.

Increasing Sales Volumes

Sales attract customers because almost everyone loves a deal. Though special marketing events such as a 48 hour sale reduce the profitability per unit, by increasing the volume sold these sales can lead to a greater profit overall.

Promoting Add-On Purchases

Having items on sale attracts customers to the store. Many times customers will not only purchase the item on sale but also, as long as they are on the premises, grab a few other items, which are regularly priced and very profitable. Like many others, you may have walked into Target to buy one item but left with five instead.

The Formula

Markdowns are no different from offering a discount. Recall from Section 6.1 that one of the types of discounts is known as a sale discount. The only difference here lies in choice of language. Markdowns are common, so you will find it handy to adapt the discount formulas to the application of markdowns, replacing the symbols with ones that are meaningful in merchandising. Formula 6.1, introduced in Section 6.1, calculates the net price for a product after it receives a single discount:

N = L × (1 − d)

Formula 6.10 adapts this formula for use in markdown situations.

In markdown situations, the selling price and the sale price are different variables. The sale price is always less than the selling price. In the event that a regular selling price has more than one markdown percent applied to it, you can extend
Formula 6.10 in the same manner that Formula 6.3 calculated multiple discounts. If you are interested in the markdown amount in dollars, recall that Formula 6.2 calculates the discount amount in dollars. Depending on what information is known, the formula has two variations:

Formula 6.2a: D$ = L × d

Formula 6.2b: D$ = L − N

Formulas 6.11a and 6.11b adapt these formulas to markdown situations.

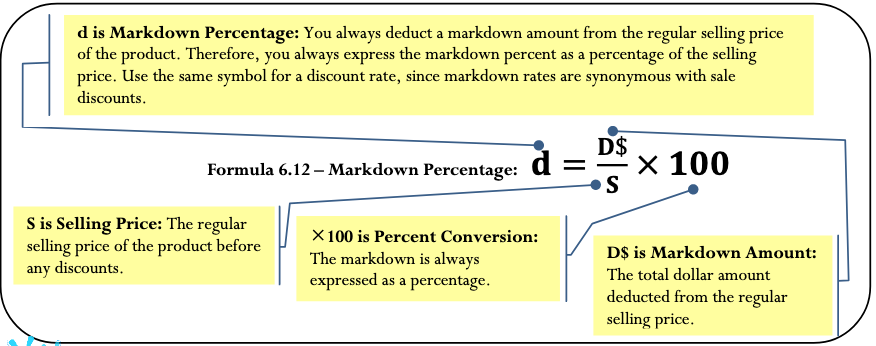
The final markdown formula reflects the tendency of businesses to express markdowns as percentages, facilitating easy comprehension and comparison. Recall Formula 6.9 from Section 6.2, which calculated a markup on selling price percent:

Formula 6.12 adapts this formula to markdown situations.

 How It Works

Follow these steps to calculate a markdown:

Step 1: Across all three markdown formulas, the four variables consist of the selling price (S), sale price (Sonsale), markdown dollars (D$), and markdown rate (d). Identify which variables are known. Depending on the known information, you may have to calculate the selling price using a combination of discount and markup formulas.

Step 2: Apply one or more of Formulas 6.10, 6.11a, 6.11b, and 6.12 to calculate the unknown variable(s). In the event that multiple markdown rates apply, extend Formula 6.10 to accommodate as many markdown rates as required.

Recall from Section 3.2 the example of the MP3 player with a regular selling price of $39.99. Assume the retailer has excess inventory and places the MP3 player on sale for 10% off. What is the sale price and markdown amount?

Step 1: The selling price and markdown percent are S = $39.99 and d = 0.10, respectively.

Step 2: Apply Formula 6.10 to calculate the sale price, resulting in Sonsale = $39.99 × (1 – 0.10) = $35.99.

Step 2 (continued): You could use either of Formulas 6.11a or 6.11b to calculate the markdown amount since the selling price, sale price, and markdown percent are all known. Arbitrarily choosing Formula 6.11a, you calculate a markdown amount of D$ = $39.99 × 0.10 = $4.00.

Therefore, if the retailer has a 10% off sale on the MP3 players, it marks down the product by $4.00 and retails it at a sale price of $35.99.

Things To Watch Out For

Just as in Section 3.2, avoid getting bogged down in formulas. Recall that the three formulas for markdowns are not new formulas, just adaptations of three previously introduced concepts. As a consumer, you are very experienced with endless examples of sales, bargains, discounts, blowouts, clearances, and the like.

Every day you read ads in the newspaper and watch television commercials advertising percent savings. This section simply crystallizes your existing knowledge. If you are puzzled by questions involving markdowns, make use of your shopping experiences at the mall!

Paths To Success

Three of the formulas introduced in this section can be solved for any variable through algebraic manipulation when any two variables are known. Recall that the triangle technique helps you remember how to rearrange these formulas, as illustrated here.

Example 3.3A: Determining the Sale Price and Markdown Amount

The MSRP for the “Guitar Hero: World Tour” video game is $189.99. Most retail stores sell this product at a price in linewith the MSRP. You have just learned that a local electronics retailer is selling the game for 45% off. What is the sale price for the video game and what dollar amount is saved?

Plan

There are two unknown variables. The first is the video game’s sale price (Sonsale). The second is the markdown amount (D$) that is realized at that sale price.

What You Already Know

Step 1: The regular selling price for the video game and the markdown rate are known:S = $189.99d = 0.45

How You Will Get There

Step 2: Calculate the sale price by applying Formula 6.10.Step 2 (continued):

Calculate the markdown amount by applying Formula 6.11b.

Perform

Step 2: Sonsale = $189.99 × (1 – 0.45)= $189.99 × 0.55 = $104.49

Step 2 (continued): D$ = $189.99 − $104.49 = $85.50

Present

The sale price for the video game is $104.49. When purchased on sale, “Guitar Hero: World Tour” is $85.50 off of its regular price.

 

Example 3.3B: Markdown Requiring Selling Price Calculation

A reseller acquires an Apple iPad for $650. Expenses are planned at 20% of the cost, and profits are set at 15% of the cost. During a special promotion, the iPad is advertised at $100 off. What is the sale price and markdown percent?

Plan

The unknown variables for the iPad are the sale price (Sonsale) and the markdown rate (d).

What You Already Know

Step 1: The pricing elements of the iPad along with the markdown dollars are known:C = $650E = 0.2CP = 0.15CD$ = $100

How You Will Get There

Step 1 (continued): Calculate the selling price of the product by applying Formula 6.5.

Step 2: Calculate the markdown percent by applying Formula 6.12:

Step 2 (continued): Calculate the sale price by applying Formula 6.11b,rearranging for Sonsale.

Perform

Step 1 (continued): S = $650 + 0.2($650) + 0.15($650) = $877.50Step 2: d = $100 × 100 = 11.396%$877.50

Step 2 (continued): $100 = $877.50 − Sonsale

Sonsale = $777.50

Present

When the iPad is advertised at $100 off, it receives an 11.396% markdown and it will retail at a sale price of $777.50.

 

Never-Ending Sales

Have you noticed that some companies always seem to have the same item on sale all of the time? This is a common marketing practice. Recall the third and fourth circumstances for markdowns. Everybody loves a sale, so markdowns increase sales volumes for both the marked-down product and other regularly priced items.For example, Michaels has a product line called the Lemax Village Collection, which has seasonal display villages for Christmas, Halloween, and other occasions. When these seasonal product lines come out, Michaels initially prices them at the regular unit selling price for a short period and then reduces their price. For Michaels, this markdown serves a strategic purpose. The company’s weekly flyers advertising the Lemax Village Collection sale attract consumers who usually leave the store with other regularly priced items.

The Formula

If an item is on sale all the time, then businesses plan the pricing components with the sale price in mind. Companies using this technique determine the unit profitability of the product at the sale price and not the regular selling price. They adapt Formula 6.5 as follows:

S = C + E + P
Sonsale = C + E + Ponsale

where Ponsale represents the planned profit amount when the product is sold at the sale price. This is not a new formula, just a new application of Formula 6.5.

How It Works

Under normal circumstances, when businesses set their selling and sale prices they follow a three-step procedure:

  • Determine the product’s cost, expenses, and profit amount.
  • Set the regular selling price of the product.
  • If a markdown is to be applied, determine an appropriate markdown rate or amount and set the sale price.

However, when a product is planned to always be on sale, businesses follow these steps instead to set the sale price and selling price:
Step 1: Set the planned markdown rate or markdown dollars. Determine the pricing components such as cost and expenses. Set the profit so that when the product is marked down, the profit amount is achieved. Alternatively, a planned markup on cost, markup on selling price, or even markup dollars may be set for the sale price.

Step 2: Calculate the sale price of the product. If cost, expenses, and profit are known, apply the adapted version of Formula 6.5. Alternatively, adapt and apply any of the other markup formulas (Formulas 6.6 through 6.9) with the understanding that the result is the sale price of the product and not the regular selling price.

Step 3: Using the known markdown rate or markdown amount, set the regular selling price by applying any appropriate markdown formula (Formulas 6.10 through 6.12).

Example

Assume for the Michael’s Lemax Village Collection that most of the time these products are on sale for 40% off. A particular village item costs $29.99, expenses are $10.00, and a planned profit of $8.00 is achieved at the sale price. Calculate the sale price and the selling price.

Step 1: The known variables at the sale price are C = $29.99, E = $10.00, P = $8.00, and d = 0.40.

Step 2: Adapting Formula 6.5, the sale price is Sonsale = C + E + Ponsale = $29.99 + $10.00 + $8.00 = $47.99. This is the price at which Michael’s plans to sell the product.

Step 3: However, to be on sale there must be a regular selling price. Therefore, if the 40% off results in a price of $47.99, apply Formula 6.10 and rearrange to get the selling price: S = $47.99 ÷ (1 – 0.40) = $79.98. Therefore, the product’s selling price is $79.98, which, always advertised at 40% off, results in a sale price of $47.99. At this sale price, Michael’s earns the planned $8.00 profit.

Important Notes

You may ask, “If the product is always on sale, what is the importance of establishing the regular price?” While this textbook does not seek to explain the law in depth, it is worth mentioning that pricing decisions in Canada are regulated by the Competition Act. With respect to the discussion of never-ending sales, the Act does require that the product be sold at a regular selling price for a reasonable period of time or in reasonable quantity before it can be advertised as a sale price. If you revisit the Michael’s example, note in the discussion that the village initially needs to be listed at the regular selling price before being lowered to the sale price.

Give It Some Thought

  • If a product has a markup on cost of 40% and a markdown of 40%, will it sell above or below cost?
  • What happens to the profit if a product that is always on sale actually sells at the regular selling price?
  • Under normal circumstances, arrange from smallest to largest: regular selling price, cost, and sale price.

Solutions

  1. Below cost, since the 40% markdown is off of the selling price, which is a larger value.
  2. The profit will be increased by the markdown amount.
  3. Cost, sale price, regular selling price.

Example 3.3C: Setting the Price in a Never-Ending Sale

An electronics retailer has 16GB USB sticks on sale at 50% off. It initially priced these USB sticks for a short period of time at regular price, but it planned at the outset to sell them at the sale price. The company plans on earning a profit of 20% of the cost when the product is on sale. The unit cost of the USB stick is $22.21, and expenses are 15% of the cost.

  1. At what price will the retailer sell the USB stick when it is on sale?
  2. To place the USB stick on sale, it must have a regular selling price. Calculate this price.
  3. If the USB stick is purchased at the regular selling price during the initial time period, how much profit is earned?

Plan

  1. This company plans on always having the product on sale, so the pricing needs to be set for the sale price, or Sonsale.
  2. You need the regular selling price, or S.
  3. Solve for the profit at the regular selling price, or P.

What You Already Know

Step 1: You know the unit cost, the retailer’s associated expenses, its planned profit at the sale price, and the markdown rate:

  • d = 0.50
  • C = $22.21
  • E = 0.15C
  • Ponsale = 0.2C

How You Will Get There

Step 2: To solve part (a), apply the adapted version of Formula 6.5: Sonsale = C + E + Ponsale

Step 3: After you know the sale price, solve part (b) by applying Formula 6.10, rearranging for S.

Step 4: Solving part (c) requires applying Formula 6.5.

Perform

Step 2:

  • Sonsale = $22.21 + 0.15($22.21) + 0.2($22.21)
  • = $22.21 + $3.33 + $4.44 = $29.98

Step 3:

  • $29.98 = S × (1 – 0.5)
  • $29.98 = S × 0.5
  • $59.96 = S

Step 4:

  • $59.96 = $22.21 + $3.33 + P
  • $59.96 = $25.54 + P
  • $34.42 = P

Present

The USB stick is on sale for $29.98, letting the company achieve its profit of $4.44 per unit. During the initial pricing period, the USB stick sells for $59.96 (its regular selling price). If a consumer actually purchases a USB stick during the initial pricing period, the electronics store earns a profit of $34.42 per unit (which is a total of the $4.44 planned profit plus the planned markdown amount of $29.96).

Exercises

Round all money to two decimals and percentages to four decimals for each of the following exercises.

Mechanics

For questions 1–6, solve for the unknown variables (identified with a ?) based on the information provided.

 

Question

 

Regular Selling Price

 

Markdown Amount

 

Markdown Percent

Sale Price

1.

$439.85

?

35%

?

2.

?

$100.00

?

$199.95

3.

$1,050.00

?

?

$775.00

4.

$28,775.00

$3,250.00

?

?

5.

?

?

33%

$13,199.95

6.

?

$38.33

12%

?

Applications

  1. A pair of Nike athletic shoes is listed at a regular selling price of $89.99. If the shoes go on sale for 40% off, what is the sale price?
  2. During its special Bay Days, The Bay advertises a Timex watch for $39.99 with a regular price of $84.99. Calculate the markdown percent and markdown amount.
  3. For spring break you are thinking about heading to Tulum, Mexico. In planning ahead, you notice that a one-week stay at the Gran Bahia Principe Tulum, regularly priced at $2,349 for air and six nights all inclusive, offers an early-bird booking discount of $350. What markdown percentage is being offered for booking early?
  4. A Heritage Infusio deep frying pan is advertised at 70% off with a sale price of $39.99. What is the frying pan’s regular selling price, and what markdown amount does this represent?
  5. A mass merchandiser uses its Lagostina cookware product line as a marketing tool. The cookware is always on sale at an advertised price of 45% off. The cost of the cookware is $199.99, expenses are $75, and the planned profit at the sale price is $110. Calculate the sale price and selling price for the cookware.
  6. Quicky Mart regularly sells its Red Bull sports drink for $2.99 per can. Quicky Mart noticed that one of its competitors down the street sells Red Bull for $1.89. What markdown percentage must Quicky Mart advertise if it wants to match its competitor.
  7. A hardware store always advertises a Masterdesigner 75-piece screwdriver set at 80% off for a sale price of $17.99.
      1. If the cost of the set is $10 and expenses are 30% of the sale price, what is the planned profit when the product is on sale?
      2. What profit is earned if the product actually sells at its regular selling price?
  1. A campus food outlet is advertising a “Buy one, get one 25% off” deal. The 25% off comes off the lower-priced item. If you purchase a chicken dinner for $8.99 and your friend gets the burger combo for $6.99, what is the markdown percentage on the total price?
  2. Blast’em Stereos purchases a stereo system for $1,900 less two discounts of 40% and 18%. The store uses this product to draw customers to the store and always offers the stereo on sale at 25% off. When the stereo is on sale, it plans on expenses equalling 30% of the cost and a profit of 20% of the sale price.
    1. What is the sale price for the stereo?
    2. How much profit does Blast’em make when the stereo sells at the sale price?
    3. By law, this stereo must sell at the regular selling price for a period of time before going on sale. What is the regular selling price?
    4. What profit does Blast’em earn if a customer purchases the stereo during this initial period?

Challenge, Critical Thinking, & Other Applications

  1. Frigid Boards purchases one of its snowboards for $395 less a retail trade discount of 15% and a loyalty discount of 4%. Its markup on selling price percentage on all snowboards is 21%. At the end of the season, any leftover snowboards are marked down by 10%. What is the sale price for the snowboard?
  2. An HP LaserJet printer has an MSRP of $399.95. It is subject to trade discounts of 30% and 23%. The LaserJet is a featured item for a computer store and is always on sale. The store plans to sell the LaserJet for a sale price that allows it to cover expenses equalling 15% of cost and realize a profit of $35.00.
    1. What is the sale price?
    2. If the MSRP is the regular unit price of the printer, what rate of markdown can the computer store advertise?
    3. What markup on selling price percentage is realized at the sale price?
  3. The Brick advertises that when you purchase a queen-size Tempur-Pedic mattress set for $2,499.97 it will give you a 51″ 3-D plasma television with a 3-D starter kit included. The value of this gift is $1,199.99. What markdown percent does this represent?
  4. A Maytag 27 cubic foot refrigerator retails for $2,400.00 at Landover Appliance Centre. The company, which is celebrating its 30th anniversary this coming weekend, features the fridge for 30% off. The markup on selling price percentage on the fridge at the regular unit selling price is 53%.
    1. What is the sale price?
    2. At the sale price, what is the markup on selling price percentage?
    3. If the expenses are 15% of the regular selling price, what is the profit when the fridge is on sale?
  5. Dreger Jewellers is selling a diamond bracelet. It uses this bracelet in its promotions and almost always has it on sale. The cost of the bracelet is $2,135 less discounts of 20% and 30%. When the bracelet is on sale for 25% off, the expenses are 15% of cost and the profit is 20% of cost.
    1. What is the sale price?
    2. What is the bracelet’s regular selling price?
    3. If the bracelet sells at the regular selling price, what are the markup amount and the markup on cost percent?

Credit: Adapted from unit 6.3 Business math: A Step-by-Step Handbook

  1. Competition Bureau, Fair Business Practices Branch, Price Scanning Report, Table B, page 5, 1999, www.competitionbureau.gc.ca/epic/site/cb-bc.nsf/en/01288e.html. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NSCC Math For Bookkeeping Copyright © 2021 by JEAN-PAUL OLIVIER and NSCC is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book