3.2 Markup: Setting the Regular Price
Need to Stay in Business
As you wait in line to purchase your Iced Caramel Macchiato at Starbucks, you look at the pricing menu and think that $4.99 seems like an awful lot of money for a frozen coffee beverage. Clearly, the coffee itself doesn’t cost anywhere near that much. But then gazing around the café, you notice the carefully applied colour scheme, the comfortable seating, the high- end machinery behind the counter, and a seemingly well-trained barista who answers customer questions knowledgeably.
Where did the money to pay for all of this come from? You smile as you realize your $4.99 pays not just for the macchiato, but for everything else that comes with it.
The process of taking a product’s cost and increasing it by some amount to arrive at a selling price is called markup. This process is critical to business success because every business must ensure that it does not lose money when it makes a sale. From the consumer perspective, the concept of markup helps you make sense of the prices that businesses charge for their products or services. This in turn helps you to judge how reasonable some prices are (and hopefully to find better deals).
The Components in a Selling Price
Before you learn to calculate markup, you first have to understand the various components of a selling price. Then, in the next section, markup and its various methods of calculation will become much clearer.
When your business acquires merchandise for resale, this is a monetary outlay representing a cost. When you then resell the product, the price you charge must recover more than just the product cost. You must also recover all the selling and operating expenses associated with the product. Ultimately, you also need to make some money, or profit, as a result of the whole process.
The Formula
Most people think that marking up a product must be a fairly complex process. It is not. Formula 6.5 illustrates the relationship between the three components of cost, expenses, and profits in calculating the selling price.
Formula 6.5
How it Works
Follow these steps to solve pricing scenarios involving the three components:
Step 1: Four variables are involved in Formula 6.5. Identify the known variables. Note that you may have to calculate the product’s cost by applying the single or multiple discount formulas (Formulas 6.1 and 6.3, respectively). Pay careful attention to expenses and profits to capture how you calculate these amounts.
Step 2: Apply Formula 6.5 and solve for the unknown variable.
Assume a business pays a net price of $75 to acquire a product. Through analyzing its finances, the business estimates expenses at $25 per unit, and it figures it can add $50 in profit. Calculate the selling price.
Step 1: The net price paid for the product is the product cost. The known variables are C = $75, E = $25, and P = $50.
Step 2: According to Formula 6.5, the unit selling price is S = C + E + P = $75 + $25 + $50 = $150.
Important Notes
In applying Formula 6.5 you must adhere to the basic rule of linear equations requiring all terms to be in the same unit. That is, you could use Formula 6.5 to solve for the selling price of an individual product, where the three components are the unit cost, unit expenses, and unit profit. When you add these, you calculate the unit selling price. Alternatively, you could use Formula 6.5 in an aggregate form where the three components are total cost, total expenses, and total profit. In this case, the selling price is a total selling price, which is more commonly known as total revenue. But you cannot mix individual components with aggregate components.
Things To Watch Out For
The most common mistake in working with pricing components occurs in the “Understand” portion of the PUPP model. It is critical to identify and label information correctly. You have to pay attention to details such as whether you are expressing the expenses in dollar format or as a percentage of either cost or selling price. Systematically work your way through the information provided piece by piece to ensure that you do not miss an important detail.
Give It Some Thought
- What three components make up a selling price? In what units are these components commonly expressed?
- In what three ways are expenses and profits expressed?
- What is the relationship between net price and cost?
Solutions
2. A specific dollar amount, a percentage of cost, or a percentage of the selling price.
3. The net price paid for a product is the same as the cost of the product.
Example 3.2A: Setting a Price on Fashion in Dollars
Mary’s Boutique purchases a dress for resale at a cost of $23.67. The owner determines that each dress must contribute$5.42 to the expenses of the store. The owner also wants this dress to earn $6.90 toward profit. What is the regular selling price for the dress?
Plan
You are looking for the regular selling price for the dress, or S.
What You Already Know
Step 1: The unit cost of the dress and the unit expense and the unit profit are all known: C = $23.67, E = $5.42, P = $6.90
How You Will Get There
Step 2: Apply Formula 6.5.
Perform
Step 2: S = $23.67 + $5.42 + $6.90 = $35.99
Present
Mary’s Boutique will set the regular price of the dress at $35.99.
Example 3.2B: Setting the Price Using Percentage of Cost
John’s Discount Store just completed a financial analysis. The company determined that expenses average 20% of the product cost and profit averages 15% of the product cost. John’s Discount Store purchases Chia Pets from its supplier for anMSRP of $19.99 less a trade discount of 45%. What will be the regular selling price for the Chia Pets?
Plan
You are looking for the regular selling price for the Chia pets, or S.
What You Already Know
Step 1: The list price, discount rate, expenses, and profit are known:
- L = $19.99
- d = 0.45
- E = 20% of cost, or 0.20C
- P = 15% of cost, or 0.15C
How You Will Get There
Step 1 (continued): Although the cost of the Chia Pets is not directly known, you do know the MSRP (list price) and the trade discount. The cost is equal to the net price. Apply Formula 6.1.
Step 2: To calculate the selling price, apply Formula 6.5.
Perform
Step 1: N = $19.99 × (1 – 0.45) = $19.99 × 0.55 = $10.99 = C
Step 2: S = $10.99 + 0.20C + 0.15C
S = $10.99 + 0.20($10.99) + 0.15($10.99)
S = $10.99 + $2.20 + $1.65 = $14.84
Present
John’s Discount Store will sell the Chia Pet for $14.84.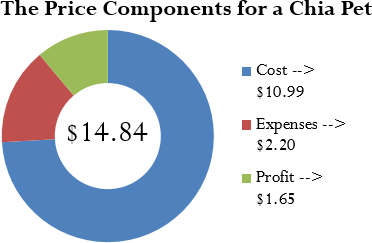 
Example 3.2C: Setting the Price Using Percentage of Selling Price
Based on last year’s results, Benthal Appliance learned that its expenses average 30% of the regular selling price. It wants a 25% profit based on the selling price. If Benthal Appliance purchases a fridge for $1,200, what is the regular unit selling price?
Plan
You are looking for the regular unit selling price for the fridge, or S.
What You Already Know
Step 1: The cost, expenses, and profit for the fridge are known:
- E = 30% of S, or 0.3
- SP = 25% of S, or 0.25
- SC = $1,200.00
How You Will Get There
Step 2: Apply Formula 6.5
Perform
Step 2: S = $1,200.00 + 0.3S + 0.25S
S = $1,200.00 + 0.55S
S − 0.55S = $1,200.00
0.45S = $1,200.00
S = $2,666.6
Present
Benthal Appliance should set the regular selling price of the fridge at $2,666.67.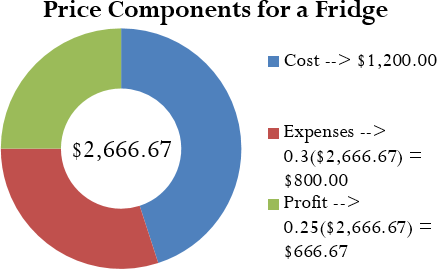 
Example 3.2D: Using Selling Price to Figure Out the Cost
If a company knows that its profits are 15% of the selling price and expenses are 30% of cost, what is the cost of an MP3 player that has a regular selling price of $39.99?
Plan
You are looking for the cost of the MP3 player, or C.
What You Already Know
Step 1: The expenses, profits, and the regular unit selling price are as follows:
- S = $39.99
- P = 15% of S, or 0.15S
- E = 30% of cost, or 0.3C
How You Will Get There
Step 2: Apply Formula 6.5, rearranging for C.
Perform
Step 2: $39.99 = C + 0.3C + 0.15($39.99)
$39.99 = 1.3C + $6.00
$33.99 = 1.3C
$26.15 = C
Present
The cost of the MP3 Player is $26.15.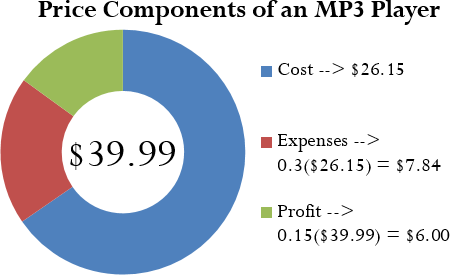 
Example 3.2E: Determining Profitability
Plan
What You Already Know
- S = $3.99
- C = $2.99
- E = 40% of cost, or 0.4C
How You Will Get There
Perform
Step 2: $3.99 = $2.99 + 0.4($2.99) + P
$3.99 = $4.19 + P
−$0.20 = P
Present
The negative sign on the profit means that Peak of the Market would take a loss of $0.20 per kilogram if it sells the strawberries at $3.99. Unless Peak of the Market has a marketing reason or sound business strategy for doing this, the company should reconsider its pricing.
Calculating the Markup Dollars
Most companies sell more than one product, each of which has different price components with varying costs, expenses, and profits. Can you imagine trying to compare 50 different products, each with three different components? You would have to juggle 150 numbers! To make merchandising decisions more manageable and comparable, many companies combine expenses and profit together into a single quantity, either as a dollar amount or a percentage. This section focuses on the markup as a dollar amount.
The Formula
One of the most basic ways a business simplifies its merchandising is by combining the dollar amounts of its expenses and profits together as expressed in Formula 6.6.
Formula 6.6
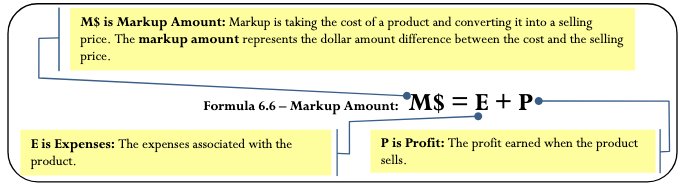
Note that since the markup amount (M$) represents the expenses (E) and profit (P) combined, you can substitute the variable for markup amount into Formula 6.5 to create Formula 6.7, which calculates the regular selling price.
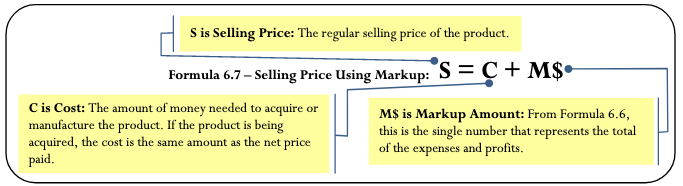
How It Works
Follow these steps when you work with calculations involving the markup amount:
Step 1: You require three variables in either Formula 6.6 or Formula 6.7. At least two of the variables must be known. If the amounts are not directly provided, you may need to calculate these amounts by applying other discount or markup formulas.
Step 2: Solve either Formula 6.6 or Formula 6.7 for the unknown variable. Recall from Example 6.2D that the MP3 player’s expenses are $7.84, the profit is $6.00, and the cost is $26.15.
Calculate the markup amount and the selling price.
Step 1: The known variables are E = $7.84, P = $6.00, and C = $26.15.
Step 2: According to Formula 6.6, the markup amount is the sum of the expenses and profit, or M$ = $7.84 + $6.00 =$13.84.
Step 2 (continued): Applying Formula 6.7, add the markup amount to the cost to arrive at the regular selling price, resulting in S = $26.15 + $13.84 = $39.99
Paths To Success
You might have already noticed that many of the formulas in this chapter are interrelated. The same variables appear numerous times but in different ways. To help visualize the relationship between the various formulas and variables, many students have found it helpful to create a markup chart [see below].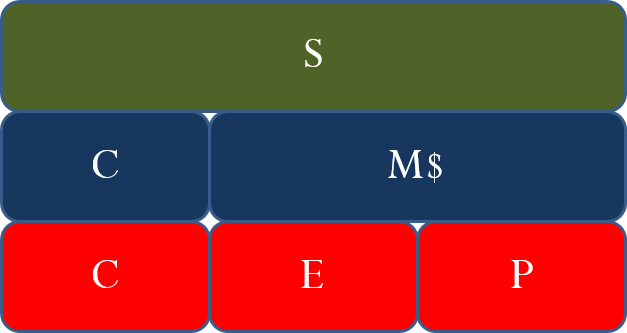
This chart demonstrates the relationships between Formulas 6.5, 6.6, and 6.7. It is evident that the selling price (the green line) consists of cost, expenses, and profit (the red line representing Formula 6.5); or it can consist of cost and the markup amount (the blue line representing Formula 6.7). The markup amount on the blue line consists of the expenses and profit on the red line (Formula 6.6).
Example 3.2F: Markup as a Dollar Amount
A cellular retail store purchases an iPhone with an MSRP of $779 less a trade discount of 35% and volume discount of 8%. The store sells the phone at the MSRP.What is the markup amount?If the store knows that its expenses are 20% of the cost, what is the store’s profit?
Plan
First of all, you need to calculate the markup amount (M$). You also want to find the store’s profit (P).
What You Already Know
Step 1: The smartphone MSRP and the two discounts are known, along with the expenses and selling price:
- L = $270 d1 = 0.35 d2 = 0.08
- E = 20% of cost, or 0.2CS = $779
How You Will Get There
Step 1 (continued): Calculate the cost of the iPhone by applying Formula 6.3.
Step 2: Calculate the markup amount using Formula 6.7.
Step 2 (continued): Calculate the profit by applying Formula 6.6, rearranging for P.
Perform
Step 1 (continued):
- N = $779.00 × (1 – 0.35) × (1 – 0.08)
- N = $779.00 × 0.65 × 0.92 = $465.84 = C
Step 2:
- $779.00 = $465.84 + M$
- $313.16 = M$
Step 2 (continued):
- $313.16 = 0.2($465.84) + P
- $313.16 = $93.17 + P
- $219.99 = P
Present
The markup amount for the iPhone is $313.16. When the store sells the phone for $779.00, its profit is$219.99.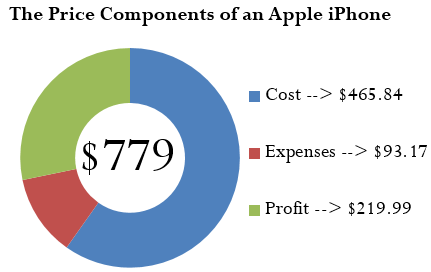 
Calculating the Markup Percent
It is important to understand markup in terms of the actual dollar amount; however, it is more common in business practice to calculate the markup as a percentage. There are three benefits to converting the markup dollar amount into a percentage:
- Easy comparison of different products having vastly different price levels and costs, to help you see how each product contributes toward the financial success of the company. For example, if a chocolate bar has a 50¢ markup included in a selling price of $1, while a car has a $1,000 markup included in a selling price of $20,000, it is difficult to compare the profitability of these items. If these numbers were expressed as a percentage of the selling price such that the chocolate bar has a 50% markup and the car has a 5% markup, it is clear that more of every dollar sold for chocolate bars goes toward list profitability.
- Simplified translation of costs into a regular selling price—a task that must be done for each product, making it helpful to have an easy formula, especially when a company carries hundreds, thousands, or even tens of thousands of products. For example, if all products are to be marked up by 50% of cost, an item with a $100 cost can be quickly converted into a selling price of $150.
- An increased understanding of the relationship between costs, selling prices, and the list profitability for any given product. For example, if an item selling for $25 includes a markup on selling price of 40% (which is $10), then you can determine that the cost is 60% of the selling price ($15) and that $10 of every $25 item sold goes toward list profits.
You can translate the markup dollars into a percentage using two methods, which express the amount either as a percentage of cost or as a percentage of selling price:
Method 1: Markup as a Percentage of Cost.
This method expresses the markup rate using cost as the base. Many companies use this technique internally because most accounting is based on cost information. The result, known as the markup on cost percentage, allows a reseller to convert easily from a product’s cost to its regular unit selling price.
Method 2: Markup as a Percentage of Selling Price.
This method expresses the markup rate using the regular selling price as the base. Many other companies use this method, known as the markup on selling price percentage, since it allows for quick understanding of the portion of the selling price that remains after the cost of the product has been recovered. This percentage represents the list profits before the deduction of expenses and therefore is also referred to as the list profit margin.
The Formula
Both formulas are versions of Formula 2.2 on rate, portion, and base. The markup on cost percentage is expressed in Formula 6.8, while the markup on selling price percentage is expressed in Formula 6.9.
How it Works
Refer back to the steps in calculating markup. The steps you must follow for calculations involving markup percent are almost identical to those for working with markup dollars:
Step 1: Three variables are required in either Formula 6.8 or Formula 6.9. For either formula, at least two of the variables must be known. If the amounts are not directly provided, you may need to calculate these amounts by applying other discount or markup formulas.
Step 2: Solve either Formula 6.8 or Formula 6.9 for the unknown variable.
Continuing to work with Example 6.2D, recall that the cost of the MP3 player is $26.15, the markup amount is $13.84, and the selling price is $39.99. Calculate both markup percentages.
Step 1: The known variables are C = $26.15, M$ = $13.84, and S = $39.99.
Step 2: To calculate the markup on cost percentage, apply Formula 6.8:
![\[ MoC \% = \frac { \$ 13.84}{ \$ 26.15} \times 100 = 52.9254 \% \]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-4edaa414ad5c64817b4618b4ff1e7b23_l3.png "Rendered by QuickLaTeX.com")
In other words, you must add 52.9254% of the cost on top of the unit cost to arrive at the regular unit selling price of $39.99. Step 2 (continued): To calculate the markup on selling price percentage, apply Formula 6.9:
![\[ MoC \% = \frac { \$ 13.84}{ \$ 39.99} \times 100 = 34.6087 \% \]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-d59f83afdb8981fdbc72d335d7d9a988_l3.png "Rendered by QuickLaTeX.com")
In other words, 34.6087% of the selling price represents list profits after the business recovers the $26.15 cost of the MP3 player.
Important Notes
Businesses are very focused on profitability. Your Texas Instruments BAII Plus calculator is programmed with the markup on selling price percentage. The function is located on the second shelf above the number three. To use this function, open the window by pressing 2nd 3. You can scroll between lines using your ↑ and ↓ arrows.
There are three variables:
- CST is the cost. Use the symbol C.
- SEL is the selling price. Use the symbol S.
- MAR is the markup on selling price percentage. Use the symbol MoS%.
As long as you know any two of the variables, you can solve for the third. Enter any two of the three variables (you need to press ENTER after each), making sure the window shows the output you are seeking, and press CPT.
Things To Watch Out For
Merchandising involves many variables. Nine formulas have been established so far, and a few more are yet to be introduced. Though you may feel bogged down by all of these formulas, just remember that you have encountered most of these merchandising concepts since you were very young and that you interact with retailers and pricing every day. This chapter merely formalizes calculations you already perform on a daily basis, whether at work or at home. The calculation of discounts is no different than going to Walmart and finding your favourite CD on sale. You know that when a business sells a product, it has to recoup the cost of the product, pay its bills, and make some money. And you have worked with percentages since elementary school.
Do not get stuck in the formulas. Think about the concept presented in the question. Change the scenario of the question and put it in the context of something more familiar. Ultimately, if you really have difficulties then look at the variables provided and cross-reference them to the merchandising formulas. Your goal is to find formulas in which only one variable is unknown. These formulas are solvable. Then ask yourself, “How does knowing that new variable help solve any other formula?”
You do not need to get frustrated. Just be systematic and relate the question to what you already know.
Paths To Success
The triangle method simplifies rearranging both Formulas 6.8 and 6.9 to solve for other unknown variables as illustrated in the figure below.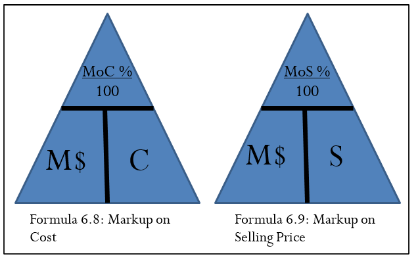
Sometimes you need to convert the markup on cost percentage to a markup on selling price percentage, or vice versa. Two shortcuts allow you to convert easily from one to the other:
![\[ MoC \% = \frac {MoS \%}{1 - MoS \%} \]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-d94429f4129a3aec1f6e11450fcbe941_l3.png "Rendered by QuickLaTeX.com")
![\[ MoS \% = \frac {MoC \%}{1 + MoC \%} \]](https://pressbooks.nscc.ca/app/uploads/quicklatex/quicklatex.com-fa603d9c704263ddcdbb554de37f8ea7_l3.png "Rendered by QuickLaTeX.com")
Notice that these formulas are very similar. How do you remember whether to add or subtract in the denominator? In normal business situations, the MoC% is always larger than the MoS%. Therefore, if you are converting one to the other you need to identify whether you want the percentage to become larger or smaller.
Key Takeaways
- To calculate MoC%, you want a larger percentage. Therefore, make the denominator smaller by subtracting MoS% from 1.
- To calculate MoS%, you want a smaller percentage. Therefore, make the denominator larger by adding MoC% to 1.
Give It Some Thought
Answer the following true/false questions.
- The markup on selling price percentage can be higher than 100%.
- The markup dollar amount can be more than the selling price.
- The markup on cost percentage can be higher than 100%.
- The markup on cost percentage in most business situations is higher than the markup on selling price percentage.
- If you know the markup on cost percentage and the cost, you can calculate a selling price.
- If you know the markup on selling price percentage and the cost, you can calculate a selling price.
Solutions
1. False. The markup amount is a portion of the selling price and therefore is less than 100%.
2. False. The markup amount plus the cost equals the selling price. It must be less than the selling price.
3. True. A cost can be doubled or tripled (or increased even more) to reach the price.
4. True. The base for markup on cost percentage is smaller, which produces a larger percentage.
5. True. You could combine Formulas 6.7 and 6.8 to arrive at the selling price.
6. True. You could convert the MoS% to a MoC% and solve as in the previous question.
Example 3.2G: Markup as a Percentage
A large national retailer wants to price a Texas Instruments BAII Plus calculator at the MSRP of $39.99. The retailer can acquire the calculator for $17.23.What is the markup on cost percentage?What is the markup on selling price percentage?
Plan
You have been asked to solve for the markup on cost percentage (MoC%) and the markup on selling price percentage (MoS%).
What You Already Know
Step 1: The regular unit selling price and the cost are provided:
- S = $39.99
- C = $17.23
How You Will Get There
Step 1 (continued): You need the markup dollars. Apply Formula 6.7, rearranging for M$.
Step 2: To calculate markup on cost percentage, apply Formula 6.8.
Step 2 (continued): To calculate markup on selling price percentage, apply Formula 6.9.
Perform
Step 1 (continued): $39.99 = $17.23 + M$
$22.76 = M$
Step 2: MoC% = $22.76/$17.23 × 100 = 132.0952%
Step 2 (continued): MoS% = $22.76/$39.99 × 100 = 56.9142%
Present
The markup on cost percentage is 132.0952%. The markup on selling price percentage is 56.9142%.
Break-Even Pricing
In running a business, you must never forget the “bottom line.” In other words, if you fully understand how your products are priced, you will know when you are making or losing money. Remember, if you keep losing money you will not stay in business for long! 15% of new businesses will not make it past their first year, and 49% fail in their first five years. This number becomes even more staggering with an 80% failure rate within the first decade.[1] Do not be one of these statistics! With your understanding of markup, you now know what it takes to break even in your business.
Break-even means that you are earning no profit, but you are not losing money either. Your profit is zero.
The Formula
If the regular unit selling price must cover three elements—cost, expenses, and profit—then the regular unit selling price must exactly cover your costs and expenses when the profit is zero. In other words, if Formula 6.5 is modified to calculate the selling price at the break-even point (SBE) with P=0, then
SBE = C + E
This is not a new formula. It just summarizes that at break-even there is no profit or loss, so the profit (P) is eliminated from the formula.
How It Works
The steps you need to calculate the break-even point are no different from those you used to calculate the regular selling price. The only difference is that the profit is always set to zero.
Recall Example 6.2D that the cost of the MP3 player is $26.15 and expenses are $7.84. The break-even price (SBE) is $26.15 + $7.84 = $33.99. This means that if the MP3 player is sold for anything more than $33.99, it is profitable; if it is sold for less, then the business does not cover its costs and expenses and takes a loss on the sale.
Example 6.2: Knowing Your Break-Even Price
John is trying to run an eBay business. His strategy has been to shop at local garage sales and find items of interest at a great price. He then resells these items on eBay. On John’s last garage sale shopping spree, he only found one item—a Nintendo Wii that was sold to him for $100. John’s vehicle expenses (for gas, oil, wear/tear, and time) amounted to $40. eBay charges a $2.00 insertion fee, a flat fee of $2.19, and a commission of 3.5% based on the selling price less $25. What is John’s minimum list price for his Nintendo Wii to ensure that he at least covers his expenses?
Plan
You are trying to find John’s break-even selling price (SBE).
What You Already Know
Step 1: John’s cost for the Nintendo Wii and all of his associated expenses are as follows:
- C = $100.00
- E (vehicle) = $40.00
- E (insertion) = $2.00
- E (flat) = $2.19
- E (commission) = 3.5%(SBE − $25.00)
How You Will Get There
Step 1 (continued): You have four expenses to add together that make up the E in the formula.
Step 2: Formula 6.5 states S = C + E + P.
Since you are looking for the break-even point, then P is set to zero and SBE = C + E.
Perform
Step 1 (continued): E = $40.00 + $2.00 + $2.19 + 3.5%(SBE − $25.00)
E = $44.19 + 0.035(SBE − $25.00) = $44.19 +0.035SBE − $0.875
E = $43.315 + 0.035SBE
Step 2:
SBE = $100.00 + $43.315 + 0.035SBE
SBE = $143.315 + 0.035SB
SBE − 0.035BE = $143.315
0.965SBE = $143.315
SBE = $148.51
Present
At a price of $148.51 John would cover all of his costs and expenses but realize no profit or loss. Therefore, $148.51 is his minimum price.
Exercises
Round all money to two decimals and percentages to four decimals for each of the following exercises.
Mechanics
For questions 1–8, solve for the unknown variables (identified with a ?) based on the information provided
| Question | Regular Unit Selling Price | Cost | Expenses | Profit | Markup Amount | Break-Even Price | Markup on Cost | Markup on Selling Price |
| 1. | ? | $188.42 | $48.53 | $85.00 | ? | ? | ? | ? |
| 2. | $999.99 | ? | 30% of C | 23% of C | ? | ? | ? | ? |
| 3. | ? | ? | ? | 10% of S | $183.28 | ? | 155% | ? |
| 4. | $274.99 | ? | 20% of S | ? | ? | ? | ? | 35% |
| 5. | ? | ? | 45% of C | ? | $540.00 | $1,080.00 | ? | ? |
| 6. | ? | $200 less 40% | ? | 15%of S | ? | ? | 68% | ? |
| 7. | ? | ? | $100.00 | ? | $275.00 | ? | 19% | |
| 8. | ? | ? | 15% of C | 12% of S | ? | $253.00 | ? | ? |
Applications
- If a pair of sunglasses sells at a regular unit selling price of $249.99 and the markup is always 55% of the regular unit selling price, what is the cost of the sunglasses?
- A transit company wants to establish an easy way to calculate its transit fares. It has determined that the cost of a transit ride is $1.00, with expenses of 50% of cost. It requires $0.75 profit per ride. What is its markup on cost percentage?
- Daisy is trying to figure out how much negotiating room she has in purchasing a new car. The car has an MSRP of $34,995.99. She has learned from an industry insider that most car dealerships have a 20% markup on selling price. What does she estimate the dealership paid for the car?
- The markup amount on an eMachines desktop computer is $131.64. If the machine regularly retails for $497.25 and expenses average 15% of the selling price, what profit will be earned?
- Manitoba Telecom Services (MTS) purchases an iPhone for $749.99 less discounts of 25% and 15%. MTS’s expenses are known to average 30% of the regular unit selling price.
-
- What is the regular unit selling price if a profit of $35 per iPhone is required?
- What are the expenses?
- What is the markup on cost percentage?
- What is the break-even selling price?
- A snowboard has a cost of $79.10, expenses of $22.85, and profit of $18.00.
-
- What is the regular unit selling price?
- What is the markup amount?
- What is the markup on cost percentage?
- What is the markup on selling price percentage?
- What is the break-even selling price? What is the markup on cost percentage at this break-even price?
Challenge, Critical Thinking, & Other Applications
- A waterpark wants to understand its pricing better. If the regular price of admission is $49.95, expenses are 20% of cost, and the profit is 30% of the regular unit selling price, what is the markup amount?
- Sally works for a skateboard shop. The company just purchased a skateboard for $89.00 less discounts of 22%, 15%, and 5%. The company has standard expenses of 37% of cost and desires a profit of 25% of the regular unit selling price. What regular unit selling price should Sally set for the skateboard?
- If an item has a 75% markup on cost, what is its markup on selling price percentage?
- A product received discounts of 33%, 25%, and 5%. A markup on cost of 50% was then applied to arrive at the regular unit selling price of $349.50. What was the original list price for the product?
- Mountain Equipment Co-op (MEC) wants to price a new backpack. The backpack can be purchased for a list price of $59.95 less a trade discount of 25% and a quantity discount of 10%. MEC estimates expenses to be 18% of cost and it must maintain a markup on selling price of 35%.
-
- What is the cost of backpack?
- What is the markup amount?
- What is the regular unit selling price for the backpack?
- What profit will Mountain Equipment Co-op realize?
- What happens to the profits if it sells the backpack at the MSRP instead?
- Costco can purchase a bag of Starbucks coffee for $20.00 less discounts of 20%, 15%, and 7%. It then adds a 40% markup on cost. Expenses are known to be 25% of the regular unit selling price.
-
- What is the cost of the coffee?
- What is the regular unit selling price?
- How much profit will Costco make on a bag of Starbucks coffee?
- What markup on selling price percentage does this represent?
- Repeat questions (a) through (d) if the list price changes to $24.00.
- Statistics Canada, “Failure Rates for New Firms,” The Daily, February 16, 2000, www.statcan.gc.ca/daily- quotidien/000216/dq000216b-eng.htm. ↵
