12 Perimeter
https://video.bccampus.ca/id/0_evlpq21e?width=608&height=402&playerId=23448552
Click play on the following audio player to listen along as you read this section.
https://video.bccampus.ca/id/0_8k8djgow?width=608&height=50&playerId=23448552

What does the word perimeter refer to? What if someone asked you to walk the perimeter of a baseball field? What does that mean?
Perimeter: A perimeter is a path that surrounds a two-dimensional object. The word comes from the Greek peri (around) and metre (measure). The term may be used either for the path or its length – it can be thought of as the length of an outline of a shape. The perimeter of a circle is called its circumference.
If you were to walk the perimeter of a baseball field you would walk around the outer edges of the field and calculate the length. If you wanted to find the perimeter of anything it would basically be like walking around the outer edge of it. Obviously we can’t do that for smaller shapes or objects but you get the idea.
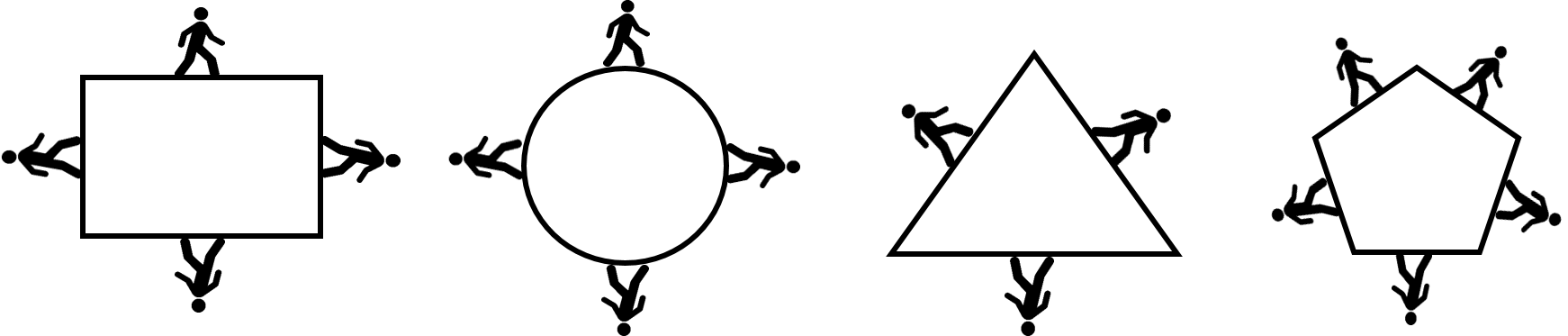
When calculating perimeter the answer will always be a linear (or one dimensional) measurement such as feet, inches, metres or centimetres.
Why would perimeter be important to us in the construction world?
Let’s say you are a carpenter and you want to put baseboard in a room. Calculating how much baseboard you need around the walls involves calculating the perimeter of the room. This would also be true for plumbers if they are putting perimeter drain around a house. Perimeter can be used in many different areas of the construction world.
The Perimeter of a Square and a Rectangle

A square and a rectangle are both similar in that they have four sides. Another characteristic that is common to both is each has four right angles. A right angle is an angle of 90 degrees.
In a square, all four sides are equal while in a rectangle the opposite sides are equal but not the adjacent sides. Calculating the perimeter of a square and a rectangle is very similar. First we’ll define what each side is called.
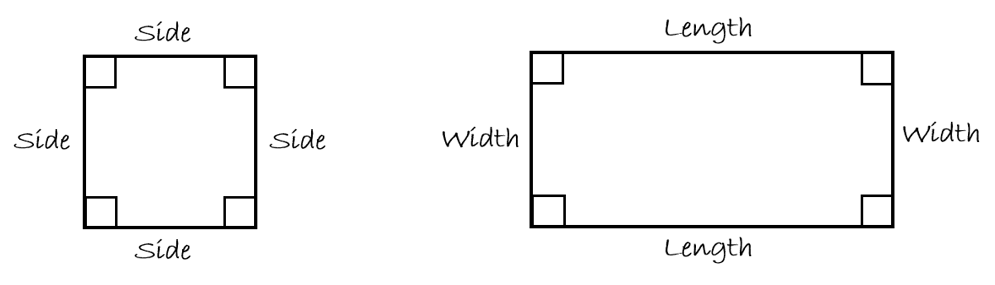
The square is straight forward as the length of each of the sides is the same, and the name of each side is simply “SIDE.” In a rectangle, the long side of the rectangle is referred to as the “LENGTH” while the shorter side is referred to as the “WIDTH.”

Before I go through calculating perimeter of a square and rectangle, take a guess at what the formula might be.


If we go back to our definition and say that the perimeter is the length that surrounds a two dimensional object, then the perimeter of both would be the length of the four sides combined.
[latex]\Large \begin{array}{ll} \textbf{Square:} & \text{Perimeter}= \text{ side}+ \text{ side} + \text{ side} + \text{ side}\\ \textbf{Rectangle:} & \text{Perimeter} = \text{length} + \text{width} + \text{width} + \text{length}\end{array}[/latex]

Would there be any other way to express the two formulas?
Take a guess.


[latex]\Large \begin{array}{ll} \textbf{Square:} & \text{Perimeter}= \text{ side} \times 4 \\ \textbf{Rectangle:} & \text{Perimeter} = (\text{length}\times 2)+(\text{width} \times 2) \end{array}[/latex]
Both versions of each formula are correct and you can use whichever you choose to answer questions.

This might be a good time to stop and discuss memorization.
Memorization is a topic that comes up quite frequently in math. Students often ask if they have to memorize formulas and for the most part the answer is yes.
Memorizing formulas can become time consuming and can also take up a lot of your brain power.
The problem that occurs when students memorize formulas is they often forget what the formula represents. Students get really good at plugging numbers into formulas but they don’t really understand what the formula does.
If the numbers were to change or the question was asked in a different manner than normal the student might become lost.
You might want to think about the following. Every time you get a formula, instead of memorizing that formula try to VISUALIZE that formula. What I mean by that is visualize what the formula represents. Hopefully it will become easier for you to work with the formula and easier for your brain to recall the formula when needed.

Example
 Find the perimeter of a square which has a side measuring 8 inches.
Find the perimeter of a square which has a side measuring 8 inches.
Step 1: Write down the formula.
[latex]\Large \text{Perimeter}= \text{ side} + \text{ side} + \text{ side} + \text{ side}[/latex]
Step 2: Solve for perimeter.
[latex]\Large \begin{array}{c} \text{Perimeter}=8+8+8+8 \\ \text{Perimeter} = 32 \text{ inches} \end{array}[/latex]
Example
Find the perimeter of a rectangle if the length is 12 and the width is 7.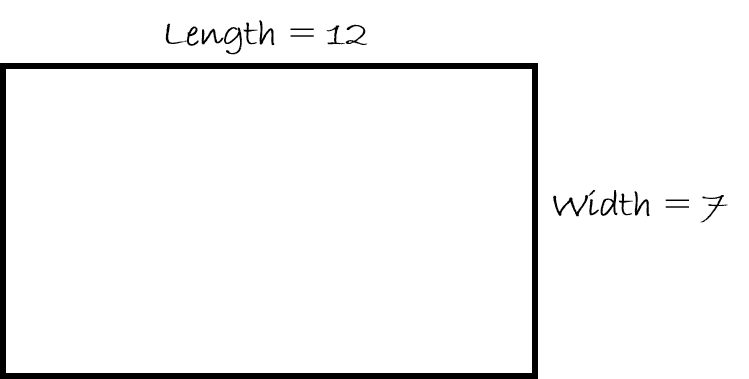
Step 1: Write down the formula
[latex]\Large \text{Perimeter} = (\text{length}\times 2) + (\text{width} \times 2)[/latex]
Step 2: Solve for perimeter
[latex]\Large \begin{array}{c} \text{Perimeter} = (7 \times 2)+(12 \times 2) \\ \text{Perimeter} = 14 + 24 \\ \text{Perimeter} =38 \end{array}[/latex]
The Perimeter of a Polygon

First of all, what is a polygon? Ever heard of one?
Definition:
A polygon is a plane figure (plane refers to it being two dimensional) with at least 3 sides and those sides must be straight.
We’ve actually already worked with polygons in this chapter. By the definition both a square and a rectangle are polygons. By definition a circle is not a polygon due to the fact that it doesn’t have straight lines.
The following are some examples of polygons…
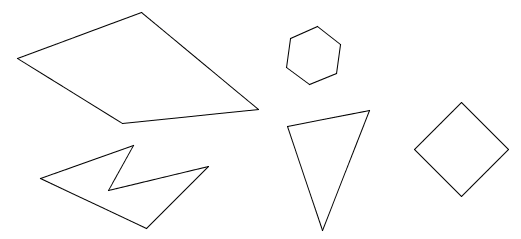
Each of the shapes is different but all have straight lines.
The question becomes: Are we going to need a different formula to calculate the perimeter of each of the shapes?
The answer: NO
So if a polygon is made up of sides, all of which are straight lines, how do you think we would calculate the perimeter?
Finding the perimeter of a polygon can be done by adding up all the sides of that polygon. And if fact we could make a generic formula for this.
Formula:
[latex]\Large \text{Perimeter of a polygon} = \text{side} + \text{ side} + \text{side and so on... }[/latex]
What the formula is saying is just add up all the sides to get the perimeter.
Example
Calculate the perimeter of the following polygon.
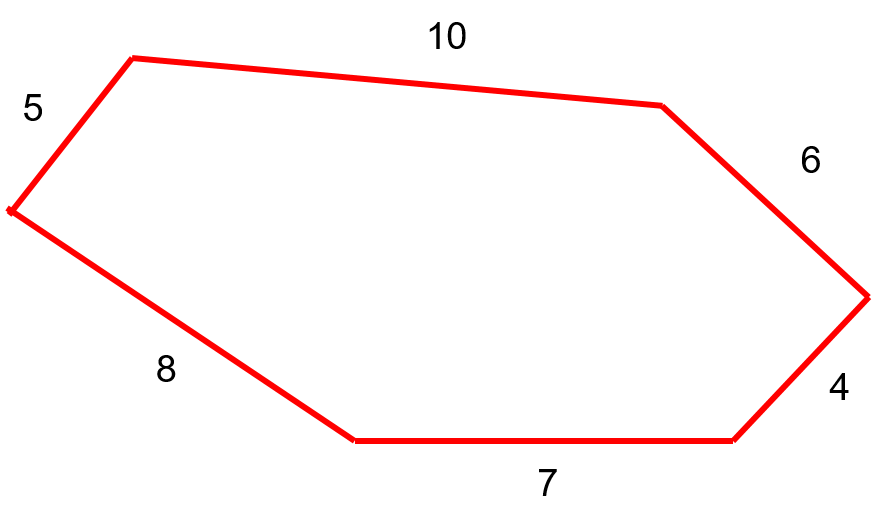
Step 1: Write down the formula
[latex]\Large \text{Perimeter of a polygon} = \text{side} + \text{ side} + \text{side and so on... }[/latex]
Step 2: Solve for perimeter
[latex]\Large \begin{array}{c} \text{Perimeter of a polygon}= 5+10+6+4+7+8 \\ \text{Perimeter}=40\end{array}[/latex]
Example
Find the perimeter of the following polygon.
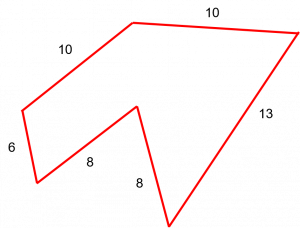
Step 1: Make sure to use the correct formula.
[latex]\large \text{Perimeter of a polygon}= \text{side} + \text{ side} + \text{ side} + \text{side} + \text{ side} + \text{ side}[/latex]
Step 2: Solve for perimeter
[latex]\Large \begin{array}{c}\text{Perimeter}=10+10+13+8+8+6 \\ \text{Perimeter} = 55 \end{array}[/latex]
Practice Questions
Try a couple practice questions for yourself. Make sure to check the video answers to see how you did.
Question 1
Jacques is a carpet layer who is going to re – carpet a room. In order to do this he has to nail a small piece of wood to the ground which runs the entire perimeter of the room. This wood is there to attach the carpet at the edges of the room.
The room itself is in the shape of a rectangle with the length being 12 feet 2 inches and the width being 10 feet 1 inch.
How much wood does Jacques need?
https://video.bccampus.ca/id/0_wyqknxvw?width=608&height=402&playerId=23448552
Question 2
Fred is a farmer who is a “jack of all trades.” Fred has to build a new fence around the farm that he owns. The area that he has to build the fence is neither a square or rectangle but has many straight sides and contains a large pond in it. Take a look at the picture below and calculate the total perimeter of the farm and pond where Fred had to construct the fence.

https://video.bccampus.ca/id/0_g6oqx35q?width=608&height=402&playerId=23448552
Perimeter of a Circle
Take a look at the circle below.
Notice anything different between the circle and the square or rectangle?
Answer: The circle doesn’t have any straight lines. It’s just one continuous line.
What we are calculating when dealing with a circle is not referred to as the perimeter but as the circumference. Essentially the circumference is the perimeter of a circle.
In order to find the circumference we need to know a thing or two about the circle. We need to know either the diameter or the radius. Take a look at the next picture to see what the diameter and radius are.
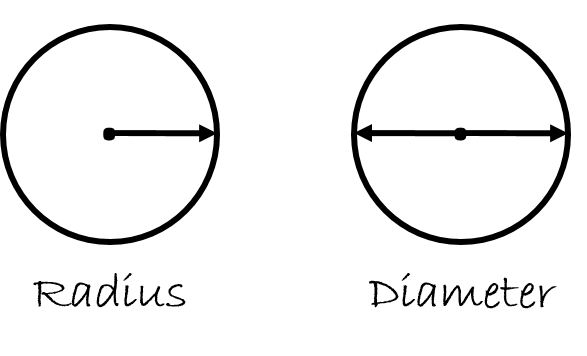
If you go to the exact center of a circle and then draw a straight line to the edge of the circle the distance measured is referred to as the radius.
If you start at any point on the edge of the circle and draw a straight line through the circle ending up on the other side, you have the diameter. Note that this straight line must go through the exact center of the circle.
As it turns out, the radius of a circle is exactly half the diameter or…
[latex]\Large \text{radius} = \dfrac{\text{diameter}}{2}[/latex]
Working with the equation we could also state that…
[latex]\Large \text{diameter} = \text{radius} \times 2[/latex]
No matter which way you work it both equations represent the relationship between the radius and diameter.
Having gotten that out of the way we can look at the formula for finding the circumference of a circle. Before I go through the formula try and take a guess at what the formula is. Once again think about the relationship between the variables and how they might work together in the formula.
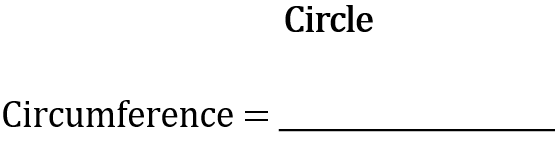

Formula:
[latex]\Large \begin{array}{c} \textbf{Circle} \\ \text{Circumference} = \pi \times \text{diameter} \end{array}[/latex]
We could also write it as…
[latex]\Large \text{C} = \pi \times \text{D}[/latex]

Hang on a minute!
What is that symbol?

Have you ever seen or heard of this symbol before?
Well it’s a constant. It’s referred to as “pi,” and if you were to sound it out, it would sound like “pie.”

What “pi” represents is the relationship between the circumference of a circle and the diameter of that same circle. “Pi” is a constant and never changes.
Having said that, the number “pi” is a bit of an anomaly. You would think that a constant would be something like 7 or maybe 12.64 or maybe even 0.00004.
“Pi” is a bit trickier than that. The following is the value of “pi.”
[latex]\Large \begin{array}{c} \pi \\ = 3.141592653589793238462643383279 \end{array}[/latex]
And that’s just the first few digits. The constant “pi” goes on forever. It doesn’t actually stop. People have figured out “pi” to thousands of digits.

The good news for us is that we don’t have to worry about all those digits that come after the decimal point. For our purpose we’ll use just the following…
[latex]\Large \pi = 3.14[/latex]

If you want to find out more about the number “pi” and how far people have calculated it, check out the following websites: Pi (Wikipedia) and 1 Million Digits of Pi (piday).
Example
Find the circumference of a circle given that its diameter is 24.
Step 1: Write down the formula.
[latex]\Large \begin{array}{c} \text{circumference} = \pi \times \text{diameter} \\ \text{OR} \\ \text{C} = \pi \times \text{D}\end{array}[/latex]
Step 2: Solve for circumference.
[latex]\Large \begin{array}{c} \text{C} = \pi \times \text{D} \\ \text{C} = 3.14 \times 24 \\ \text{C} = 75.36 \end{array}[/latex]
Example
Find the circumference of a circle given that its radius is 8.
Step 1: Write down the formula.
[latex]\Large \text{C} = \pi \times \text{D}[/latex]
 The formula calls for the diameter but we are given the radius. We have to use the relationship between radius and diameter to find the diameter.
The formula calls for the diameter but we are given the radius. We have to use the relationship between radius and diameter to find the diameter.
[latex]\Large \begin{array}{c} \text{diameter} = \text{radius} \times 2 \\ \text{diameter} = 8 \times 2 \\ \text{diameter} = 16 \end{array}[/latex]
Step 2: Solve for circumference.
[latex]\Large \begin{array}{c} \text{C} = \pi \times \text{D} \\ \text{C} = 3.14 \times 16 \\ \text{C} = 50.24 \end{array}[/latex]

We’re going to take the difficulty up a step here, and we’ll need to use the rules of transposing in the last section to help us out.
Example
Find the diameter of a circle given that the circumference is exactly 153.
Step 1: Write down the formula.
[latex]\Large \text{circumference} = \pi \times \text{diameter}[/latex]
Step 2: Rework the formula to solve for diameter.
[latex]\Large\text{diameter}= \dfrac{\text{circumference}}{\pi}[/latex]
Step 3: Solve for diameter.
[latex]\Large \begin{array}{c} \text{diameter}= \dfrac{\text{circumference}}{\pi} \\ \text{diameter} = \dfrac{153}{3.14} \\ \text{diameter} = 48.73 \end{array}[/latex]
Practice Questions
Try a couple practice questions for yourself. Make sure to check the video answers to see how you did. Note: Check out the “SO WHAT” video at the end of the practice questions before you head over to the next section.
Question 1

Haley is a Red Seal welder and is fabricating stainless steel tanks for a food storage facility. The radius of the tanks is 24 inches. What is the circumference of the tanks going to be?
https://video.bccampus.ca/id/0_wiuh2hzm?width=608&height=402&playerId=23448552
Question 2

Floyd is a concrete worker who is building a foundation for a cabin. The cabin and wraparound deck are supported by round concrete footings. The radius of each footing has been engineered to be 4 inches. What is the circumference of the footings?
https://video.bccampus.ca/id/0_0xt4r655?width=608&height=402&playerId=23448552

