6 Pressure Measurements
https://video.bccampus.ca/id/0_3jmo2ks8?width=608&height=402&playerId=23448552
Click play on the following audio player to listen along as you read this section.
https://video.bccampus.ca/id/0_y48hvw3f?width=608&height=50&playerId=23448552

Dealing with the pressures of life can certainly be a balancing act. There is family, work, money and all the other fun stuff that makes up life. How would you describe that pressure?
The pressure we’re going to talk about in this section differs from the pressures of everyday life.
The word pressure actually has a few different definitions. The version we are going to work with goes something like this:

Pressure: The force exerted by an object on another object or the force exerted by an object per unit area. That area could be any area you could come up with but for the most part we use a square inch or a square metre.
When dealing with pressure our starting point is going to be pounds per square inch (psi). Pounds per square inch is the imperial version of pressure and the one most of us are most likely familiar with. We use this measurement when dealing with things like pumping up car or bike tires or when dealing with water pressure.

The most common metric version of pressure is known as the Pascal (Pa) and quite often we put Pascals into groups of 1000 and just like the metric system likes to do it’s called a kilopascal (kPa). Now as pressure is defined as force per unit area we should define what a Pascal actually is. One Pascal is equal to a pressure of one Newton per metre square (n/m2) where a Newton is a measure of force.
If we want to get technical here is the definition of what a newton is.
Newton: is the force needed to move (or accelerate) an object weighing one kilogram at one metre per second squared.
We can also include pounds in the idea of force where pounds can be defined as a unit of force as well. It is sometimes referred to as pounds-force or lbf.
Whatever the case we basically have our two measurements of force to work with. One being the Pascal (Pa) (or kilopascal(kPa)) and the other being pounds per square inch (psi).
Those are not the only pressure measurements that we’ll deal with. Another couple of pressure measurements that are common in the world of trades are inches of water column and feet of head.
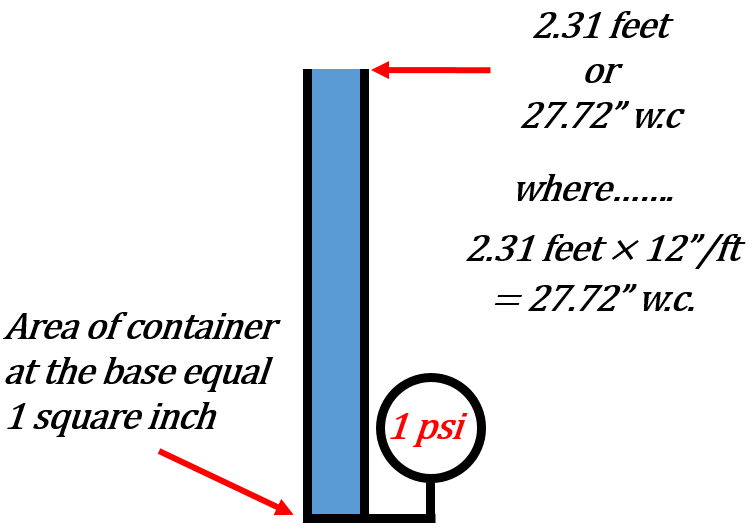
Both are in reference to a column of water. The idea is that having a column of water creates a pressure at the base of the column. The higher the column of water the greater the pressure. One pound per square inch is equivalent to having a column of water 2.31 feet in height. The pressure at the base of that column of water would be 1 psi. As it turns out 27.72 inches is equal to 2.31 feet so if we had a column of water 27.72 inches (2.31 feet) we would have a pressure of one pound per square inch at the base of that column of water.
If you are wondering if this will work for other liquids the answer is yes. Inches of mercury (Hg) is another common way to measure pressure.
Inch of mercury (Hg): This one we might actually use as its common when measuring a vacuum. We would be required to measure vacuum for such things as vacuum pumps in medical facilities or to measure vacuum in refrigeration systems. 2.04 inches of mercury is equal to 1 pound per square inch.
Let’s throw in another few examples of ways pressure can be expressed.
Bar: Approximately the average pressure at sea level. (It’s actually 1.013 Bar). It’s also equivalent to 100,000 Pascals.
Torr: Was originally meant to be equal to 1 mmHg but it’s not quite that anymore. It is now defined as 1/760 of an atmosphere where one atmosphere is defined as 101.325 kPa. One atmosphere is essentially the pressure at sea level exerted on all objects. You might sometimes also hear it referred to as standard atmospheric pressure. Standard atmospheric pressure is also known to be 14.7 psi.
In any event a Torr is roughly equal to 133.32 Pascals.
Let’s put all the main players when dealing with pressure into a table with the starting point being one pound per square inch.
One pound per square inch equals:
- 6.895 kilopascals (kPa)
- 2.04 inches of mercury (Hg)
- 2.31 feet of head (ft/hd) (water)
- 27.72 inches of water column (″ w.c.)
As we have done in the previous parts of the chapter it’s time to go through some examples working between these numbers.
Example
How many kilopascals are there in 10 psi?
Step 1: Find the number that works for kilopascals and psi. In this case:
[latex]\Large \text{1 psi} = 6.895 \text{ kilopascals}[/latex]
Step 2: As usual build a ratio
[latex]\Large \dfrac{\text{1 psi}}{\text{10 psi}} = \dfrac{6.895 \text{ kPa}}{\text{X kPa}}[/latex]
Step 3: Cross multiply
[latex]\Large \begin{array}{c} \dfrac{\text{1 psi}}{\text{10 psi}} = \dfrac{6.895 \text{ kPa}}{\text{X kPa}} \\ 1 \times \text{X} = 10 \times 6.895 \\ \text{X} = 68.95 \\ \text{Answer} = 68.95 \text{ kPa} \end{array}[/latex]
Example
How many pounds per square inch are there in 150 kilopascals?
Step 1: Find a number that works for kilopascals and psi.
[latex]\Large \text{1 psi} = 6.895 \text{ kilopascals}[/latex]
Step 2: Build a ratio.
[latex]\Large \dfrac{\text{1 psi}}{\text{X psi}} = \dfrac{6.895 \text{ kPa}}{\text{150 kPa}}[/latex]
Step 3: Cross multiply.
[latex]\Large \begin{array}{c} \dfrac{\text{1 psi}}{\text{X psi}} = \dfrac{6.895 \text{ kPa}}{\text{150 kPa}} \\ 1 \times 150 = \text{X} \times 6.895 \\ \text{X} = \dfrac{150}{6.895} = 21.75 \\ \text{Answer} = 21.75 \text{ psi} \end{array}[/latex]
Example
A column of water has a pressure at the base of 14 pounds per square inch. What is that pressure in feet of head (ft/hd)?
Step 1: Find a number that works for psi and feet of head.
[latex]\Large 1 \text{ psi} = 2.31 \text{ feet of head}[/latex]
Step 2: Build a ratio.
[latex]\Large \dfrac{1 \text{ psi}}{14 \text{ psi}} = \dfrac{2.31 \text{ ft/hd}}{\text{X ft/hd}}[/latex]
Step 3: Cross multiply.
[latex]\Large \begin{array}{c} \dfrac{1 \text{ psi}}{14 \text{ psi}} = \dfrac{2.31 \text{ ft/hd}}{\text{X ft/hd}} \\ 1 \times \text{X} = 14 \times 2.31 \\ \text{X} = 32.34 \\ \text{Answer} = 32.34 \text{ ft/hd}\end{array}[/latex]
Now change that feet of head into inches of water column.
Step 1: Find a number that works between feet of head and inches of water column.

Do you see a problem? The issue here is that we don’t have a number than translates between the two of them. Although we could figure this number out mathematically it would mean that in the end we would have a lot more numbers to remember.
The solution here is to find a number that they both relate to and that number is pounds per square inch. What we can then do is go from feet of head to pounds per square inch and then from pounds per square inch to inches of water column.

Step 2 (really step 1): We first need to change the feet of head to psi.
[latex]\Large 1 \text{ psi} = 2.31 \text{ feet of head}[/latex]
Step 3: Build a ratio.
[latex]\Large \dfrac{1 \text{ psi}}{\text{X psi}} = \dfrac{2.31 \text{ ft/hd}}{32.34 \text{ ft/hd}}[/latex]
Step 4: Cross Multiply.
[latex]\Large \begin{array}{c}\dfrac{1 \text{ psi}}{\text{X psi}} = \dfrac{2.31 \text{ ft/hd}}{32.34 \text{ ft/hd}} \\ 1 \times 32.34 = \text{X} \times 2.31 \\ \text{X} = \dfrac{32.34}{2.31} = 14 \\ \text{Answer} = 14 \text{ psi}\end{array}[/latex]
What you’ll notice here is that we are back to where we started from. We actually just proved that our first calculation was correct.
Step 5: Change the pounds per square inch into inches of water column. Find the number that translates between those two.
[latex]\Large 1 \text{ psi} = 27.72 \text{ ″ w.c.}[/latex]
Step 6: Build a ratio.
[latex]\Large \dfrac{\text{1 psi}}{\text{14 psi}} = \dfrac{27.72 \text{ ″ w.c.}}{\text{X ″ w.c.}}[/latex]
Step 7: Cross multiply.
[latex]\Large\begin{array}{c} \dfrac{\text{1 psi}}{\text{14 psi}} = \dfrac{27.72 \text{ ″ w.c.}}{\text{X ″ w.c.}} \\ 1 \times \text{X} = 14 \times 27.72 \\ \text{X} = 388.08 \\ \text{Answer} = 388.08 \text{ ″ w.c.}\end{array}[/latex]
Practice Questions
Try a couple of practice questions yourself and check the video answers to see how you did.
Question 1

Adam and Riley are both gas fitters and today they are installing a new boiler in a warehouse. They checked the gas pressure gauge leading into the warehouse and it reads 34.5 kilopascals. What is that in pounds per square inch?
https://video.bccampus.ca/id/0_tuxpzr8r?width=608&height=402&playerId=23448552
Question 2

Zhang Wei is a plumber originally from China. He is now a plumber in Canada and has decided to specialize in hydronic heating. He is required to buy a circulating pump that puts out 32 feet of head. As he is used to working in pounds per square inch he wants to translate 32 feet of head into psi. How many psi is going to be required from the pump?
https://video.bccampus.ca/id/0_2yias29c?width=608&height=402&playerId=23448552

