Click play on the following audio player to listen along as you read this section.

https://video.bccampus.ca/id/0_9621ifc1?width=608&height=50&playerId=23448552

The units in the previous part of this section dealt with heat energy measurement. The answers we were calculating indicated an amount or quantity of heat. When measuring temperature we are not measuring quantity but instead we are gauging the intensity of the heat.

For example going outside on a day when it’s −10°C feels colder or much more intense that going outside on a day that is +20°C.

How much heat content would you think there is at −10°C? Honestly who cares? Just get inside and we can sort that out later.

If I were to ask you what units you generally associated with temperature what would you say?

I’m guessing most of you would respond with either Celsius or Fahrenheit. Those would be the two most common methods of describing the heat here in Canada and as Canada uses the metric system we would most likely be seeing the temperature in Celsius.

But have you ever heard of the Kelvin temperature scale or the Rankine temperature scale?

Well these temperature scales are based on what is known as “absolute temperature.”

If you go on the internet and look up absolute temperature you can get some pretty convincing definitions, some of which we might actually be able to comprehend. Basically, the absolute temperature scale starts at absolute zero and a simplified definition of absolution zero would be the following:

ABSOLUTE ZERO: The temperature at which all molecular movement ceases to exist.

As there is no molecular movement there is also no heat generated by the molecules.

If you want to know more about absolute zero check out the link: Absolute Zero (Wikipedia) 

So what we start with are the Celsius scale which is the metric version of temperature and the Fahrenheit scale which is the imperial version. You might notice that when you are watching T.V. in Canada you will see much smaller temperature numbers than when you watch T.V. from a U.S. channel. This is due to the fact that if we took a temperature reading on the Fahrenheit scale and found a similar temperature on the Celsius scale the Celsius temperature reading would work out to be much smaller.

For example we could look at room temperature.

[latex]\Large \text{Metric} = {20}^{\circ} \text{ Celsius} \qquad \text{Imperial} = {68}^{\circ} \text{ Fahrenheit}[/latex]

On another note does anyone watch T.V. anymore or is it just the internet and Netflix? Anyway, back to Celsius and Fahrenheit.

What we want to do here is relate the metric and imperial scale with each other and then add the absolute scale equivalents. We’ll start with the boiling point of water.

Water boils at 100°C and 212°F. Note the letter “C” represents Celsius while the letter F represent Fahrenheit.

Next we find the freezing point of water. Water freezes at 0°C and at 32°F. We can put all those together into a small drawing.

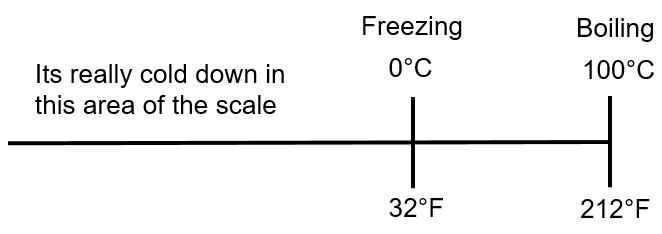
We’ll go through how to go from Celsius to Fahrenheit and back in just a bit but before we get to that we should add the absolute temperature scales.

If we were to add them to our drawing it would look something like the following.

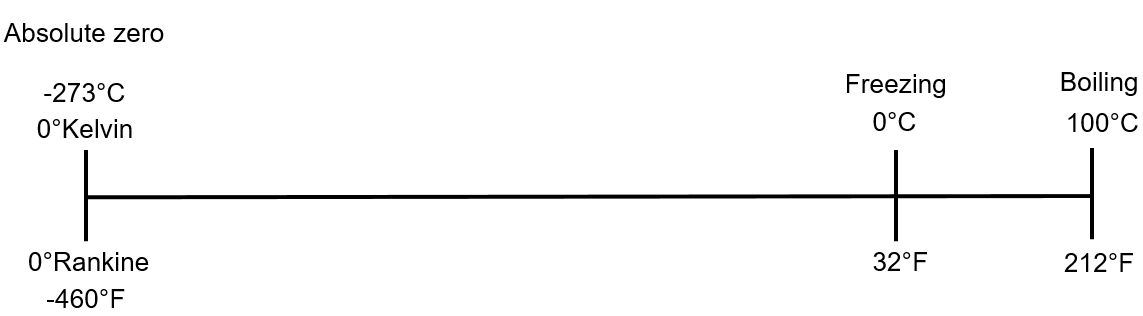
Note that it’s not drawn exactly to scale. If it were then absolute zero would be a little farther to the left. Remember that absolute zero is where there is no molecular movement and therefore no heat generated.

We’ll start with Celsius and Kelvin. What you’ll note from the drawing above is that 0°K, also known as absolute zero, is −273°C.

What’s also important to note is that 1°K is −272°C.

What that indicates is that a one degree change in Kelvin is equal to a one degree change in Celsius.

If I were to go from −273°C to 0°C this would be a change of 273 degrees. On the Kelvin scale it would have gone from 0°K to 273°K.

Fahrenheit and Rankine follow a similar pattern. Absolute zero on the Rankine scale is 0°R while on the Fahrenheit scale it’s −460°F.

Once again we would find that 1°R is −459°F indicating that a one degree change in Rankine is equal to a one degree change in Fahrenheit.

If we would apply this idea to the imperial temperature scales we would get the following. To go from −460°F to 0°F would be a change of 460°. On the Rankine scale it would have gone from 0°R to 460°R.

How we deal with this mathematically is the following:

[latex]\Large \begin{array}{c} \text{°Kelvin} = \text{°Celsius} + 273\\ \text{°Rankine} = \text{°Fahrenheit} + 460 \end{array}[/latex]

Let’s go through a couple examples going from one to the other. These are going to be fairly straight forward so we won’t go through all the steps like we usually do.

Celsius to Fahrenheit and Fahrenheit to Celsius

This is probably what we’ve all been waiting for here in this part of the chapter. Going back and forth between Celsius and Fahrenheit is probably the most common temperature calculation tradespeople are required to make.

We could be dealing with gas fitting appliances and have to calculate temperature rise through the appliance in either Celsius or Fahrenheit. We may have to change numbers in code books from one designation to the other. If you are a cook or a baker you might be dealing with a recipe that states the oven temperature in Celsius but your oven only has Fahrenheit on it. In all cases being able to translate between the two temperature scales in important.

If we are going to change Celsius to Fahrenheit the formula is as follows:

[latex]\Large \text{°Fahrenheit} = \text{°Celsius} \times \dfrac{9}{5} + 32[/latex]

There are a couple of things to note here. One is the order the calculation needs to be done. The first thing to be done here is to multiply the degree Celsius by 9/5. After that add the 32.

Doing it this way follows the rules of math and in the next chapter we go through a thorough explanation of those rules. For now just follow the path laid out.

The second thing to note is that the fraction can also be stated as a number. Writing out the formula using a number instead of a fraction would look like this:

[latex]\Large \begin{array}{rl} \text{First:} \quad & \dfrac{9}{5} = 1.8 \\ \text{Then:} \quad & \text{°Fahrenheit} = \text{°Celsius} \times 1.8 + 32 \end{array}[/latex]

You can use either of the two formulas as they both end up with the same answer. It just depends on which one you are more comfortable using.

Now let’s go through a couple examples.

Practice Questions

Try a couple of practice questions yourself and check the video answers to see how you did.