1.E Dividing Whole Numbers
Chad Flinn and Mark Overgaard
Harpreet has ended up with a total of 12 jobs on the go. He has decided to hire 3 more people to help him with all the work. They are Dixon, Kavanir, and Arman. He now has 4 employees including Jamieson and he splits the jobs evenly between the 4 of them. How many jobs will each of them be doing?
This would be an example of dividing whole numbers. Harpreet has a total of 12 jobs and he has 4 employees splitting the number of jobs evenly. We would write this as:
[latex]\LARGE12÷4=?[/latex]
How would we go about solving this? Well let’s look at it visually to start. We have 12 jobs to work with.

What we do now when dividing is take the number we have (12) and split it into the number of groups we are going to have. In this case we have 4 employees so we will split it into 4 even groups.
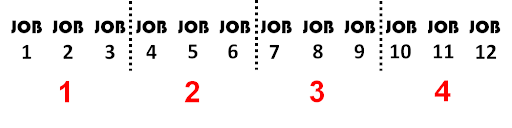
You can now count that there are 3 jobs in every group. So what we get in the end is:
[latex]\LARGE12÷4=3[/latex]
Like multiplying, dividing small whole numbers is usually pretty straight forward. But what if we had a case where we have larger numbers. How would you go about doing this calculation without the use of a calculator?
What we use is a system called “LONG DIVISION” and it looks something like the following:
Example
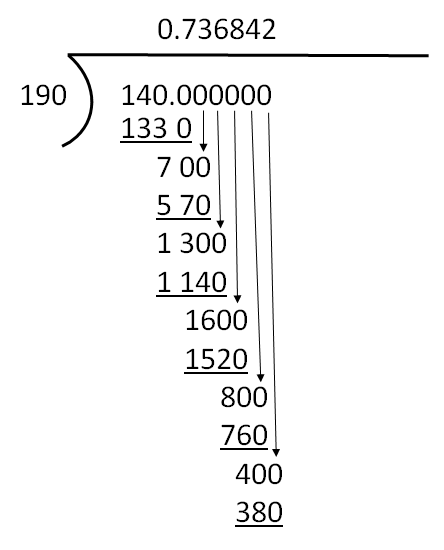
We’ll use this process of long division to answer the following question. How many times does 5 go into 90?
Step 1: Set up the equation in a workable form.
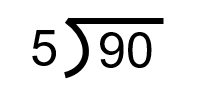
![]()
Note: the symbol to the left is used to designate a long division question. The placement of the five in the equation indicates that it is the number to be divided into the 90. Essentially, the equation is asking how many times 5 can go into 90.
Step 2: Take the 5 and divide it into the first digit in the number to be divided into. In this case this is the 9. We have to figure out how many times 5 goes into 9 without going over.
This is where knowing our times tables really comes in handy. We know that:
[latex]\LARGE5\times1=5[/latex]
and
[latex]\LARGE5\times2=10[/latex]
Therefore we know that 5 goes into 9 one complete time with 4 left over.
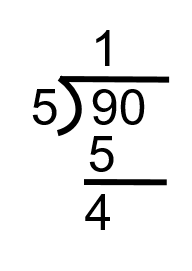
To complete this step we need to bring down the next number in the equation. In this case, it’s the 0. What we have now is 40 and the next step becomes how many times 5 goes into 40.
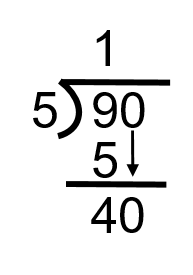
Step 3: Figure out how many times 5 goes into 40 without going over. If we go back to our multiplying, we might be able to remember that 5 goes into 40 exactly 8 times.
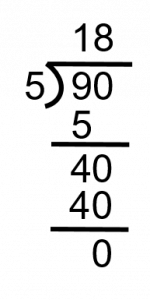
As we end up with zero there are no more numbers to work with through which means we are done.
Try another example.
Example
How many times does 7 go into 167?
Step 1: Set up the equation in a workable form.
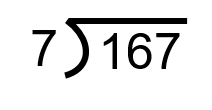
Step 2: Take the 7 and divide it into the first digit in the number to be divided into. In this case this is the 1, and we can see that this is not going to work. As such, we just move one step to the right and divide the 7 into 16.
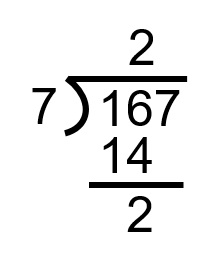
To complete this step we need to bring down the next number in the equation. In this case it’s the 7. We now have 27 and the next step becomes how many times 7 goes into 27.
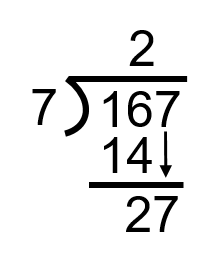
Step 3: Figure out how many times 7 goes into 27 without going over.
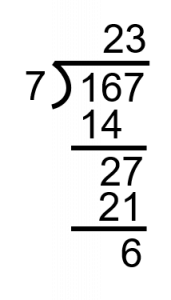
We end up with a little different scenario here than in the first question. When we get to the end of the question we have 6 left over. What this is telling us is that 7 goes into 167 twenty three times with 6 left over.
Practice Questions
Try a couple example questions yourself and check the video answers to see how you did. Remember to set the question up in a format that works.
Question 1
[latex]\LARGE130÷8=[/latex]
Question 2
[latex]\LARGE684÷12=[/latex]

