2 Adding and Subtracting Fractions
Adding Fractions with Common Denominators

Abigail, Hanna, and Naomi are studying for their midterm exam. The material they are required to study consists of 16 chapters of reading. The three of them realize that 16 chapters is a lot of reading for each of them to do, so they decide to study in a more efficient manner. They come up with a plan in which each of them reads a certain number of chapters and then summarizes it for the other two. They will share notes, and each will find online videos corresponding to their particular set of chapters.
Now, the chapters are not created equally. Some are quite easy, while others are much tougher. Their goal is to spread the workload evenly between the three of them. Remember that there are 16 chapters.
Abigail has the highest number of chapters to go through with 6. Hanna has 5, while Naomi has only 4. If you were to add those up, you would notice that that only comes to 15 chapters. The last chapter in the book is about troubleshooting electrical systems, and the apprentices decide that they will go through that one together.
We can represent each of their workloads as a fraction of a whole:
[latex]\LARGE\text{Abigail has }\dfrac{6}{16}[/latex]
[latex]\LARGE\text{Hanna has }\dfrac{5}{16}[/latex]
[latex]\LARGE\text{Naomi has }\dfrac{4}{16}[/latex]
What if were to add those fractions? It would look something like this:
[latex]\LARGE\dfrac{6}{16}+\dfrac{5}{16}+\dfrac{4}{16}=?[/latex]
What you’ll note is that the numerators are all different, while the denominators are all the same (16). When adding or subtracting fractions, the denominators must be the same. We refer to this as having a common denominator.
So, in order to get the answer to the above question, you just add all the numerators. Adding fractions is very simple in this respect.
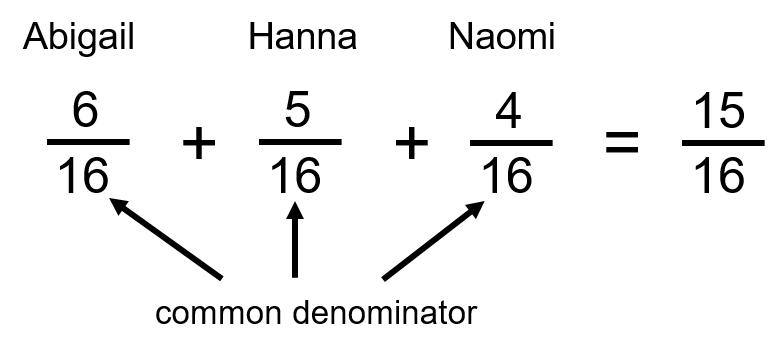
Notice that the denominator in the final answer is the same as that in the fractions being added. By the end, the apprentices will have gone through 15 of the 16 chapters separately, and then they will go through the last chapter together.
The concept of adding fractions with common denominators is easy enough, and we did enough adding whole numbers that going through examples at this point might not be worth it (but if you need a review, see Adding Whole Numbers). What we will do instead is write down some examples of adding fractions so you can see the idea.
[latex]\LARGE\dfrac{1}{8}+\dfrac{2}{8}=\dfrac{3}{8}[/latex]
[latex]\LARGE\dfrac{5}{16}+\dfrac{6}{16}=\dfrac{11}{16}[/latex]
[latex]\LARGE\dfrac{13}{32}+\dfrac{11}{32}=\dfrac{24}{32}[/latex]

Do you notice anything about the answer to the last one? It can be reduced.
[latex]\LARGE\dfrac{24}{32}\longrightarrow\dfrac{2}{3}[/latex]
Before we get going any further with work on fractions, this might be a good time to state that, when working with fractions, we generally want to put the answer in lowest terms.
Subtracting Fractions with Common Denominators
What about subtracting fractions? Well, it follows the same principle: you must have a common denominator, and then you subtract the numerators. Here are some examples of subtracting fractions:
[latex]\LARGE\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}[/latex]
[latex]\LARGE\dfrac{9}{16}-\dfrac{5}{16}=\dfrac{4}{16}\longrightarrow\dfrac{1}{4}[/latex]
[latex]\LARGE\dfrac{27}{32}-\dfrac{14}{32}=\dfrac{13}{32}[/latex]
Adding and Subtracting Fractions with Uncommon Denominators
We’re going to step it up a bit now. Our examples of adding and subtracting fractions are fairly straightforward, due to the fact that the denominators are the same. A more difficult situation involves adding or subtracting fractions that have different denominators. Take a look at the following example:
[latex]\LARGE\dfrac{1}{2}+\dfrac{3}{8}=?[/latex]
We can’t simply add up the numerators and the denominators, as it just won’t work. Take a look at the two circles drawn below. One is split into 2 parts, and one is split into 8 parts. Do you notice anything about the sizes of the parts?
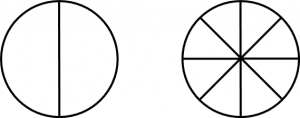

You’ll note that the parts in the 2-part circle are much larger than those in the 8-part circle. If we were to add up the parts in each of the circles, it would be like adding apples and oranges.
So the idea becomes making it so that the parts we are adding are the same size. If we can somehow get to that point, then we are good to go, and we can add the two fractions. This is referred to as finding a common denominator, and most often, we try and find the lowest common denominator.
Lowest common denominator: The lowest number that two denominators can evenly go into.
Take a look at the equation below. One of the denominators is 2, while the other is 8.
[latex]\LARGE\dfrac{1}{2}+\dfrac{3}{8}=?[/latex]
The process here is similar to when we were putting fractions into their lowest terms in the last section, only this time, we will be increasing at least one of the denominators, and sometimes, we will be increasing both until we find one that is common. What we are looking for is a number that both denominators can go into evenly. In this example, we see that 2 can go into 8 and 8 can go into 8. This leaves us with a common denominator of 8.
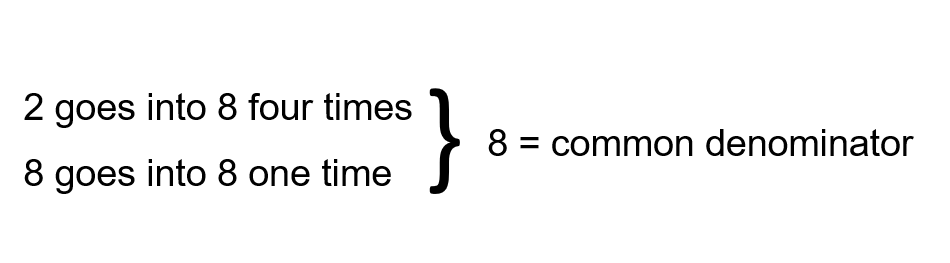
We have determined that 8 is going to be our common denominator, which means that one of the fractions is already good to go.

But what about 1 over 2, or one-half? We have to turn the one-half into a fraction with 8 as the denominator.
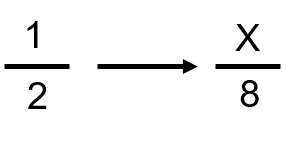
As we calculated above, 2 goes into 8 four times.
[latex]\LARGE2\times4=8[/latex]
That’s good for the denominator, but what about the numerator? Well, whatever we do to the one part of the fraction, we must do the same to the other part. This leaves the fraction with the same value. We then have to also multiply the 1 by 4.
[latex]\LARGE1\times4=4[/latex]
If we wanted to do it all in one step, it would look something like this:
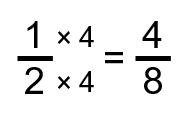
Now we have something we can work with. Go back to the original equation and replace the [latex]\dfrac{1}{2}[/latex] with [latex]\dfrac{4}{8}[/latex].
[latex]\LARGE\dfrac{4}{8}+\dfrac{3}{8}=\dfrac{7}{8}[/latex]
Okay, so that works for adding fractions, but what about subtracting fractions? Well, subtracting fractions follows the same principle: if the denominators are not the same, then we have to find a common denominator first before subtracting the two fractions.
Example
Calculate the following:
[latex]\LARGE\dfrac{7}{8}-\dfrac{13}{16}=[/latex]
Step 1: Find the common denominator. This can get a little tricky when the numbers begin to get larger. As you get more familiar with the patterns in numbers, the answers will come easier. The question we are asking right now is, “What number can both 8 and 16 go into evenly?”
We might even start by seeing if the smaller denominator can go into the larger denominator. In this case, it does.
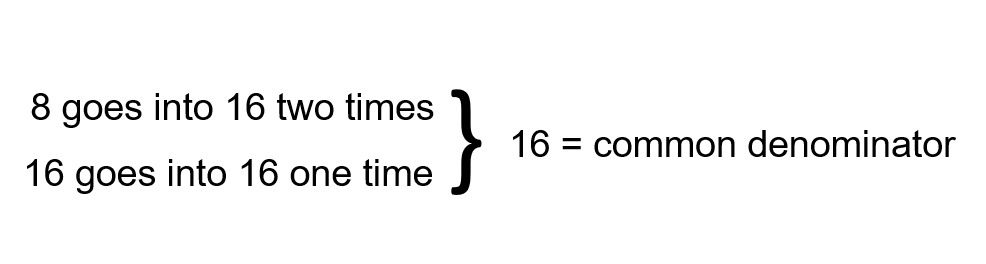
The fraction with the common denominator of 16 is already good to go, but we have to work with the fraction with a denominator of 8.
Step 2: Multiply both the numerator and the denominator of ⅞ by 2 to give the fraction the common denominator of 16.
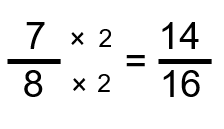
Step 3: Subtract the new versions of the fractions.
[latex]\LARGE\dfrac{14}{16}-\dfrac{13}{16}=\dfrac{1}{16}[/latex]
Practice Questions
Answer the following practice questions and check for the video answers. Make sure to put each answer into its lowest terms or a mixed number, if necessary.
Question 1
[latex]\LARGE\dfrac{3}{16}+\dfrac{5}{8}=[/latex]
https://video.bccampus.ca/id/0_535fcxuh?width=608&height=402&playerId=23448552
Question 2
[latex]\LARGE\dfrac{5}{8}-\dfrac{5}{16}=[/latex]
https://video.bccampus.ca/id/0_1765fg0o?width=608&height=402&playerId=23448552
Question 3
[latex]\LARGE\dfrac{1}{2}+\dfrac{7}{8}=[/latex]
https://video.bccampus.ca/id/0_8s54ppy3?width=608&height=402&playerId=23448552
Question 4
[latex]\LARGE2\dfrac{1}{2}+1\dfrac{7}{8}=[/latex]
https://video.bccampus.ca/id/0_clcs9eo0?width=608&height=402&playerId=23448552

Wait a minute! That last question stepped it up a notch by adding mixed numbers. I know you’ve already taken a look at the video answer, but let’s take a step back and go through the motions of adding and subtracting mixed numbers. We’ll start with a short explanation.
Adding or Subtracting Mixed Numbers
The issue we run into when adding or subtracting mixed numbers is that a mixed number is composed of two separate parts: there is the whole number, and then there is the fraction. When adding the numbers, this can be straightforward, like the following:
[latex]\LARGE4\dfrac{3}{8}+3\dfrac{2}{8}=7\dfrac{5}{8}[/latex]
Pretty straightforward, right? You simply add the two whole numbers, and then add the fractions. It works out quite nicely. But what about a situation like the next example?
[latex]\LARGE4\dfrac{5}{8}+3\dfrac{4}{8}=?[/latex]
Do you see the issue?
The issue (it’s not really an issue) is that, when we add the fractions, we end up with a bigger number in the numerator than in the denominator.
[latex]\LARGE4\dfrac{5}{8}+3\dfrac{4}{8}=7\dfrac{9}{8}[/latex]
The solution is to change the improper fraction part of the answer into a mixed number, and then add that to the whole number part of the answer.
[latex]\LARGE\dfrac{9}{8}\longrightarrow1\dfrac{1}{8}[/latex]
Take the 7 and add it to the mixed number to get our final answer.
[latex]\LARGE7+1\dfrac{1}{8}=8\dfrac{1}{8}[/latex]
Okay, that seemed pretty straightforward, but what about subtraction? Well, we follow the same rules. Take a look at the following example:
Example
[latex]\LARGE8\dfrac{7}{8}-6\dfrac{3}{8}=?[/latex]
The procedure is similar to that for adding fractions, but instead of adding, we are subtracting. We can break it down into two parts. We start by subtracting the whole numbers, and then follow that up by subtracting the fractions portion.
Step 1: Subtract the whole numbers.
[latex]\LARGE8-6=2[/latex]
Step 2: Subtract the fractions portion of the equation.
[latex]\LARGE\dfrac{7}{8}-\dfrac{3}{8}=\dfrac{4}{8}\rightarrow\dfrac{1}{2}[/latex]
Step 3: Put it all together.
[latex]\LARGE8\dfrac{7}{8}-6\dfrac{3}{8}=2\dfrac{4}{8}\rightarrow2\dfrac{1}{2}[/latex]
Okay, not too hard, right? But take a look at the next example and see if you can figure out the problem that we are going to have as we run through it.
Example
[latex]\LARGE5\dfrac{2}{8}-3\dfrac{7}{8}=?[/latex]
The problem emerges not when you are subtracting the whole numbers, but when you are subtracting the fractions.
[latex]\LARGE\dfrac{2}{8}-\dfrac{7}{8}=?[/latex]
We would end up with an answer less than zero. This is not going to work for us. So how do we solve the problem? Well, the answer lies in borrowing, and what we are borrowing from is the whole number, 5. Let’s just say we borrow 1 from the 5. This would leave us with 4, and then what? Take a look at the following logic.
[latex]\LARGE5=4+1[/latex]
[latex]\LARGE1=\dfrac{8}{8}[/latex]
If we go ahead and break the 5 down into 4 and 1, and then split that 1 down into parts of 8, we have a lot more eighths to work with. We can now put everything together to get the following:
[latex]\LARGE5\dfrac{2}{8}=4+\dfrac{8}{8}+\dfrac{2}{8}=4\dfrac{10}{8}[/latex]
We now have numbers we can work with in our original question.
[latex]\LARGE4\dfrac{10}{8}-3\dfrac{7}{8}=?[/latex]
We now follow the same steps as before.
Step 1: Subtract the whole numbers.
[latex]\LARGE4-3=1[/latex]
Step 2: Subtract the fractions portion of the equation.
[latex]\LARGE\dfrac{10}{8}-\dfrac{7}{8}=\dfrac{3}{8}[/latex]
Step 3: Put it all together.
[latex]\LARGE4\dfrac{10}{8}-3\dfrac{7}{8}=1\dfrac{3}{8}[/latex]
Practice Questions
Add or subtract the following mixed numbers, making sure to put your answer in lowest terms. Check the video answers at the end to see how you did.
Question 1
[latex]\LARGE7\dfrac{3}{16}+4\dfrac{5}{16}=[/latex]
https://video.bccampus.ca/id/0_s8dew6mc?width=608&height=402&playerId=23448552
Question 2
[latex]\LARGE2\dfrac{7}{16}+3\dfrac{7}{8}=[/latex]
https://video.bccampus.ca/id/0_nxy48mwt?width=608&height=402&playerId=23448552
Question 3
[latex]\LARGE8\dfrac{27}{32}-1\dfrac{15}{32}=[/latex]
https://video.bccampus.ca/id/0_tbjhhjze?width=608&height=402&playerId=23448552
Question 4
[latex]\LARGE6\dfrac{5}{16}-5\dfrac{5}{8}=[/latex]
https://video.bccampus.ca/id/0_zomyq5wz?width=608&height=402&playerId=23448552

