15 Convert Fractions to Decimals

We just learned how to change fractions to decimals, and now it’s time to do the opposite. How do you think this is done? If you guessed that it’s the reverse of what we just did, then you are right. We’ll start by going through an example dealing with fractions to decimals, and then move onto changing feet, inches, and fractions of an inch to feet and decimals of a foot.
What we are looking to do is go from:
[latex]\LARGE\dfrac{1}{2}\text{ to }0.5[/latex]
Once again, the quick and easy way to do this is to go through a few examples. Start with a plain old fraction and work towards changing this into a decimal.
[latex]\LARGE\dfrac{3}{8}[/latex]
This can be done a number of ways, with the simplest being:
[latex]\LARGE3÷8=0.375[/latex]
You could plug the numbers into your calculator, or you could use long division to come up with the answer.
That’s it. You’re done!

Okay, that was pretty easy, but now let’s move on to an example that is a bit more difficult. We are going to change a number written in feet, inches, and fractions of an inch into a decimal.
Example
Change this number into a decimal:
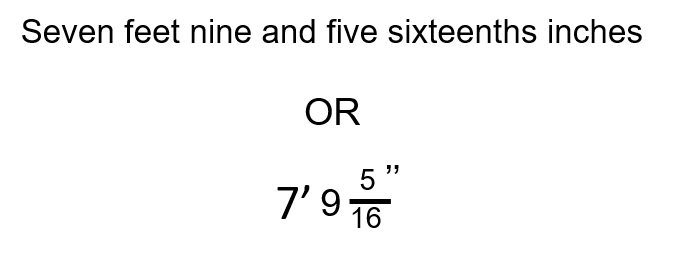
Step 1: Identify any part of the number that is already in a form that works. In this case, the 7 feet is good to go and nothing needs to be done with it.


Step 2: Take the fraction of an inch and turn it into a decimal.
[latex]\LARGE\dfrac{5}{16}\text{ OR }5÷16=0.3125[/latex]
Pause here for a moment and ask yourself what unit the 0.3125 is in. All we have done is change the fraction of an inch into decimals of an inch. We now have turned the 9 inches and fractions of an inch into 9 inches and decimals of an inch.
[latex]\LARGE9\dfrac{5}{16}\text{ inches into }9.3125\text{ inches}[/latex]
Step 3: Change the inches and decimals of an inch into decimals of a foot using the fact that 1 foot = 12 inches.

In the last section, when we went from decimals to fractions, we multiplied by 12 to get inches. As we are doing the reverse calculation here by going from fractions to decimals, we end up dividing by 12 inches to get decimals of a foot.
[latex]\LARGE9.3125÷12=0.776[/latex]
Once again, ask yourself what units you end up with here. When we take the inches and divide it by 12, we end up with feet or, in this case, decimals of a foot. So our final answer becomes:
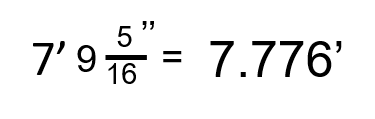
We’ll go through another example, and then let you try a couple on your own after that.
Example
Change the following number written in feet, inches, and fractions of an inch into feet and decimals of a foot.
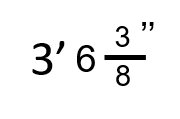
Step 1: Identify any part of the number that is already in a form that works. In this case, the 3 feet is good to go and nothing needs to be done with it.
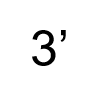

Step 2: Take the fraction of an inch and turn it into a decimal.
[latex]\LARGE\dfrac{3}{8}\text{ OR }3÷8=0.375[/latex]
Put the inches and decimals of an inch together.
[latex]\LARGE6\dfrac{3}{8}\text{ inches into }6.375\text{ inches}[/latex]
Step 3: Change the inches and decimals of an inch into decimals of a foot using the fact that 1 foot = 12 inches.
[latex]\LARGE6.375÷12=0.531[/latex]
So our final answer becomes:
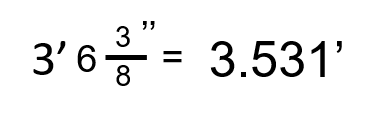
Practice Questions
Change the following feet, inches, and fractions of an inch into feet and decimals of a foot. Check the video answers to make sure you are on the right track.
Question 1
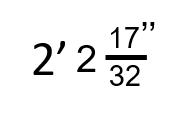
https://video.bccampus.ca/id/0_n3ejv8mt?width=608&height=402&playerId=23448552
Question 2
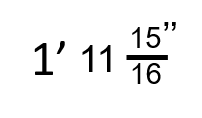
https://video.bccampus.ca/id/0_612e14f7?width=608&height=402&playerId=23448552

