11.9 Discounts

NSCC; Lumen Learning

11.9 Discounts

Discounts

You mutter in exasperation, “Why can’t they just set one price and stick with it?” Your mind boggles at all the competing discounts you encounter at the mall in your search for that perfect Batman toy for your nephew. Walmart is running their Rollback promotion and is offering a Batmobile for 25% off, regularly priced at $49.99. Toys R’ Us has an outlet in the parking lot where the regular price for the same toy is $59.99, but all Batman products are being cleared out at 40% off. You head over to The Bay for a warehouse clearance event that has the same toy priced at $64.99 but at 35% off. It is also Bay Days, which means you can scratch and win a further 10% to 20% off the sale price. You go to Dairy Queen for a Blizzard to soothe your headache while you figure things out.

The cost of a product is the amount of money required to obtain the merchandise. If you are a consumer, the ticketed price tag on the product is your cost. If you are a reseller (also known as a middleman or intermediary), what you pay to your supplier for the product is your cost. If you are a manufacturer, then your cost equals all of the labour, materials, and production expenditures that went into creating the product.

A discount is a reduction in the price of a product. As a consumer, you are bombarded with discounts all the time. Retailers use various terms for discounts, including sales or clearance. If your business purchases a product from a supplier, any discount it receives lowers how much the business pays to acquire the product. When a business buys products, the price paid is the cost to the business. Therefore, a lower price means a lower cost.

If your business is the one selling the product, any discount offered lowers the selling price and reduces revenue per sale. Since the revenue must cover all costs and expenses associated with the product, the lower price means that the business reduces profits per sale. In business, it is common practice to express a discount as a percentage off the regular price.

How Distribution and Pricing Work

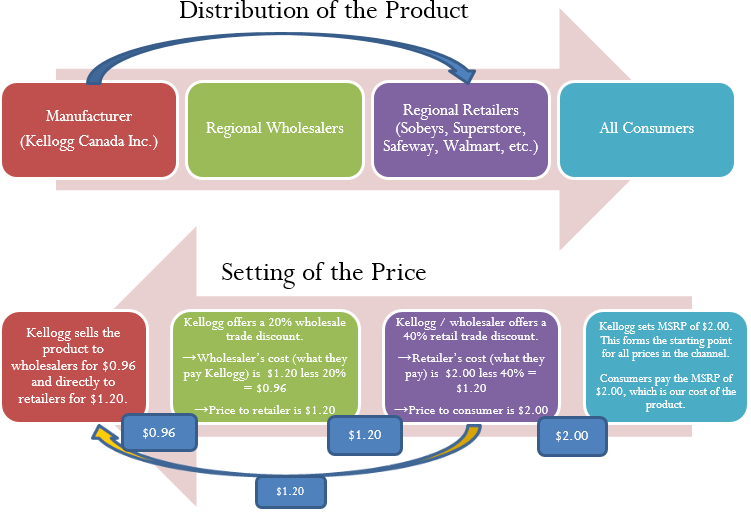
A diagram depicting the processes of distribution of the product and setting of the price. Distribution: the product is distributed from the manufacturer (eg. Kellogg Canada Inc.) to regional wholesalers, who then distribute the product to regional retailers (eg. Sobeys, Superstore, Safeway, Walmart), who distribute the product to all consumers. The steps of setting a product’s price are as follows: Step One: A manufacturer such as Kellogg sets MSRP of $2.00. This forms the starting point for all prices in the channel. Consumers pay the MSRP of $2.00, which is our cost of the product. Step Two: Kellogg/wholesaler offers a 40% retail trade discount. The retailer’s cost (what they pay) is $2.00 less 40% = $1.20. Step Three: Kellogg offers a 20% wholesale trade discount. The wholesaler’s cost (what they pay Kellogg) is $1.20 less 20% = $0.96. Step 4: Kellogg sells the product to wholesalers for $0.96 and directly to retailers for $1.20.

Start with distribution in the top half of the figure and work left to right. As an example, let’s look at a manufacturer such as Kellogg Canada Inc. (which makes such products as Pop-Tarts, Eggo Waffles, and Rice Krispies). Kellogg’s Canadian production plant is located in London, Ontario. To distribute its products to the rest of Canada, Kellogg Canada uses various regional wholesalers. Each wholesaler then resells the product to retailers in its local trade area; however, some retailers (such as the Real Canadian Superstore) are very large, and Kellogg Canada distributes directly to these organizations, bypassing the wholesaler as represented by the blue arrow. Finally, consumers shop at these retailers and acquire Kellogg products.

The relationship of distribution to pricing is illustrated in the bottom half of the figure, working right to left. For now, focus on understanding how pricing works; the mathematics used in the figure will be explained later in this chapter. Kellogg Canada sets a manufacturer’s suggested retail price, known as the MSRP. This is a recommended retail price based on consumer market research. Since grocery retailers commonly carry thousands or tens of thousands of products, the MSRP helps the retailer to determine the retail price at which the product should be listed. In this case, assume a $2.00 MSRP, which is the price consumers will pay for the product.

The retailer must pay something less than $2.00 to make money when selling the product. Kellogg Canada understands its distributors and calculates that to be profitable most retailers must pay approximately 40% less than the MSRP. Therefore, it offers a 40% discount. If the retailer purchases directly from Kellogg, as illustrated by the yellow arrow, the price paid by the retailer to acquire the product is $2.00 less 40%, or $1.20. Smaller retailers acquire the product from a wholesaler for the same price. Thus, the retailer’s cost equals the wholesaler’s price (or Kellogg Canada’s price if the retailer purchases it directly from Kellogg).

The wholesaler’s price is $1.20. Again, Kellogg Canada, knowing that the wholesaler must pay something less than $1.20 to be profitable, offers an additional 20% discount exclusively to the wholesaler. So the price paid by the wholesaler to acquire the product from Kellogg Canada is $1.20 less 20%, or $0.96. This $0.96 forms Kellogg Canada’s price to the wholesaler, which equals the wholesaler’s cost.

In summary, this discussion illustrates two key pricing concepts:

Companies higher up in the distribution channel pay lower prices than those farther down the channel. Companies receive discounts off the MSRP based on their level in the distribution system. This may result in multiple discounts, such as a wholesaler receiving both the retailer’s discount and an additional discount for being a wholesaler.
One organization’s price becomes the next organization’s cost (assuming the typical distribution channel structure):
Manufacturer’s Price = Wholesaler’s Cost
Wholesaler’s Price = Retailer’s Cost
Retailer’s Price = Consumer’s Cost

Single Discounts

Let’s start by calculating the cost when only one discount is offered. Later in this section you will learn how to calculate a cost involving multiple discounts.

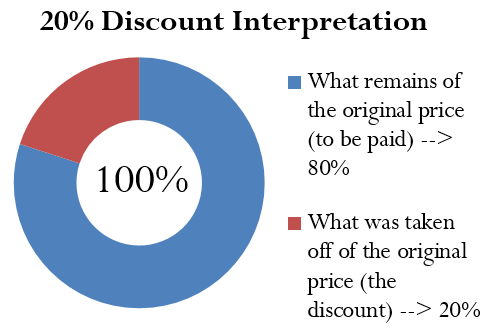
Figuring out the price after applying a single discount is called a net price calculation. When a business calculates the net price of a product, it is interested in what you still have to pay, not in what has been removed. Note in Formula 1.1 below that you take 1 and subtract the discount rate to determine the rate owing. If you are eligible for a 20% discount, then you must pay 80% of the list price, as illustrated in the figure below:

A circle diagram illustrating a 20% discount. The circle represents the total cost of the product (100%). The red section of the circle illustrates the discount, or what was taken off the original price (20%). The remaining blue portion of the circle illustrates what remains to be paid of the original price (80%).

Formula 1.1 – Single Discount

$N= L\times(1-d)$

$N$ is the Net Price: The price of the product after the discount is removed from the list price. It is a dollar amount representing what price remains after you have applied the discount.

$L$ is the List Price: The normal or regular dollar price of the product before any discounts. It is the Manufacturer’s Suggested Retail Price (MRSP).

$d$ is the Discount Rate: The percentage (in decimal format) of the list price that is deducted.

Formula 1.1 includes rate, portion, and base, where the list price is the base, the $(1 − d)$ is the rate, and the net price represents the portion of the price to be paid.

Formula 1.2a and Formula 1.2b – Discount Amount

Formula 1.2a

$D\char36=L\times d$

Formula 1.2b

$D\char36=L-N$

$D\char36$ is Discount Amount: Determine the discount amount in one of two ways, depending on what information is known:
If the list price and discount rate are known, apply Formula 1.2a.
If the list price and net price are known, apply Formula 1.2b.

$L$ is List Price: The dollar amount of the price before any discounts.

$N$ is Net Price: The dollar amount of the price after you have deducted all discounts.

$d$ is Discount Rate: The percentage (in decimal format) of the list price to be deducted. This time, you are interested in figuring out the amount of the discount, therefore you do not take it away from 1.

Notice that Formula 1.1 requires the discount to be in a percentage (decimal) format; sometimes a discount is expressed as a dollar amount, though, such as “Save $5 today.” Formulas 1.2a and 1.2b relate the discount dollar amount to the list price, discount percent, and net price. Choose one formula or the other depending on which variables are known.

How It Works

Follow these steps to calculate the net price involving a single discount. These steps are adaptable if the net price is a known variable and one of the other variables is unknown.

Step 1: Identify any known variables, including list price, discount rate, or discount amount.

Step 2: If the list price is known, skip this step. Otherwise, solve for list price using an appropriate formula.

Step 3: Calculate the net price.

If the list price and discount are are known, apply Formula 1.1.
If the list price and discount amount are known, apply Formula 1.2b and rearrange for $N$ .

Assume a product sells for $10 and is on sale at 35% off the regular price. Calculate the net price for the product.

Step 1: The list price of the product is $L = \char36 10$ . It is on sale with a discount rate of $d = 0.35$ .

Step 2: List price is known, so this step is not needed.

Step 3: Applying Formula 1.1 results in a new price of

$N=\char36 10\times(1-0.35)= \char36 6.50$ .

Note that if you are interested in learning the discount amount, you apply Formula 1.2b to calculate:

$D\char36 =\char36 10-\char36 6.50=\char36 3.50$ .

A circle diagram illustrating the net price of a product. The circle represents the list price ($10.00). The red portion of the circle represents the discount, or what you save (35% or $3.50.) The blue portion of the circle illustrates the net price, or what you pay ($6.50.)

You can combine Formula 1.1 and either version of Formula 1.2 in a variety of ways to solve any single discount situation for any of the three variables. As you deal with increasingly complicated pricing formulas, your algebraic skills in solving linear equations and substitution become very important.

Many of the pricing problems take multiple steps that combine various formulas, so you need to apply the PUPP model systematically. In any pricing problem, you must understand which variables are provided and match them up to the known formulas. To get to your end goal, you must look for formulas in which you know all but one variable. In these cases, solving for variables will move you forward toward solving the overall pricing problem.

If you find you cannot produce a formula with only one unknown variable, can you find two formulas with the same two unknowns? If so, recall from Chapter 1 that you can use your algebraic skills to find the roots of the two equations simultaneously. Alternatively, you can solve one formula for a variable then substitute it into the other formula, allowing you to isolate the remaining variable. Throughout the examples in this chapter you will see many applications of these algebraic skills.

Remember to apply the rounding rules:

1. Until you arrive at the final solution, avoid rounding any interim numbers unless you have some special reason to do so.
2. Round all dollar amounts to the nearest cent. If the dollar amount has no cents, you may write it either without the cents or with the “.00” at the end.
3. Round all percentages to four decimals when in percent format.

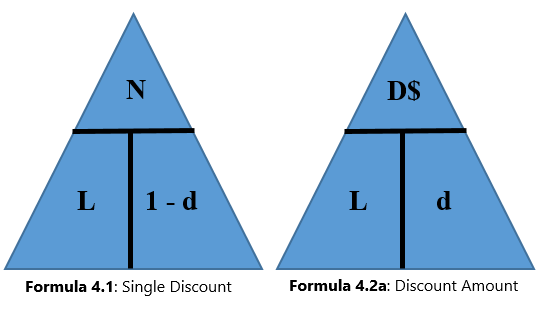
When working with single discounts, you are not always solving for the net price. Sometimes you must calculate the discount percent or the list price. At other times you know information about the discount amount but need to solve for list price, net price, or the discount rate. The triangle technique can remind you how to rearrange the formulas for each variable, as illustrated in the figure below.

Two triangle diagrams illustrating how to rearrange formulas. The triangle on the left illustrates formula 4.1: single discount. The top sector of the triangle contains the variable N. The left sector of the triangle contains the variable L. The right sector of the triangle contains the variable (1-d). The triangle on the right illustrates formula 4.2a: discount amount. The top sector of the triangle contains the variable D$. The left sector of the triangle contains the variable L. The right sector of the triangle contains the variable d.

Give It Some Thought:

Will you pay more than, less than, or exactly $10.00 for a product if you are told that you are paying:
a. a net price of $10.00 when there is a discount of 25%?
b. a list price of $10.00 when there is a discount of 25%?
If an item is subject to a 40% discount, will the net price be more than or less than half of the list price of the product?

Example 1.1A – Determining the Retailer’s Net Price for a Pair of Jeans

A manufacturer that sells jeans directly to its retailers uses market research to find out it needs to offer a 25% trade discount. In doing so, the retailers will then be able to price the product at the MSRP of $59.99. What price should retailers pay for the jeans?

Plan:
Calculate how much a retailer should pay for the jeans after the regular price has been discounted to accommodate the trade discount. This is called the net price for the product, or $N$ .

Understand:
Step 1: The list price and the discount rate are known.

$L= \char36 59.99$
$d = 0.25$

Step 2: List price is known, so skip this step.

Step 3: Apply Formula 1.1

Perform:
Step 3:

$N=\char36 59.99\times(1-0.25)=\char36 59.99\times0.75=\char36 44.99$

Present:
The manufacturer should sell the jeans to the retailers for $44.99.

Example 1.1B – Determining the List Price of a Jacket

Winners pays a net price of $27.50 for a winter jacket after receiving a retail trade discount of 45%. What was the MSRP of the jacket?

Plan:
Calculate the MSRP for the jacket before Winners received the retail trade discount to arrive at the net price. This is called the list price for the product, or $L$ .

Understand:
Step 1: The net price and the discount rate are known:

$N = \char36 27.50$
$d = 0.45$

Step 2: List price is the unknown variable; skip this step.

Step 3: Apply Formula 1.1, rearranging for L.

Perform:
Step 3:

$\begin{array}{r} \char36 27.50=L(1-0.45)\\ L=\char36 27.50\div(1-0.45)\\ L=\char36 27.50\div0.55=\char36 50.00 \end{array}$

Present:
The MSRP, or list price, of the winter jacket is $50.00.

Example 1.1C – Determining the Discount Percent and Discount Amount

You are shopping at Mountain Equipment Co-op for a new environmentally friendly water bottle. The price tag reads $14.75, which is $10.24 off the regular price. Determine the discount rate applied.

Plan:
You need to find out how the sale price translates into the discount rate, or $d$ .

Understand:
Step 1: The discount amount and net price are known:

$D\char36 = \char36 10.24$
$N = \char36 14.75$

Step 2: Use Formula 1.2b to calculate the list price, rearranging for $L$ .

Step 3: Convert the discount amount into a percentage by applying Formula 1.2a, rearranging for $d$ .

Perform:
Step 2:
List price:

$\begin{array}{r} \char36 10.24=L-\char36 14.75\\ L = \char36 24.99 \end{array}$

Step 3:
Discount rate:

$d=D\char36\div L$

$\begin{array}{r} d=\frac{\char36 10.24}{\char36 24.99}=0.409764&{\textrm{ or }}&40.9764\% \end{array}$

Present:
The water bottle today has been reduced in price by the amount of $10.24. This represents a sale discount of 40.9674%.

Multiple Discounts

You are driving down the street when you see a large sign at Old Navy that says, “Big sale, take an additional 25% off already reduced prices!” In other words, products on sale (the first discount) are being reduced by an additional 25% (the second discount). Because Formula 1.1 handles only a single discount, you must use an extended formula in this case.

Businesses commonly receive more than one discount when they make a purchase. Consider a transaction in which a business receives a 30% trade discount as well as a 10% volume discount. First, you have to understand that this is not a 30% + 10% = 40% discount. The second discount is always applied to the net price after the first discount is applied. Therefore, the second discount has a smaller base upon which it is calculated. If there are more than two discounts, you deduct each subsequent discount from continually smaller bases. Formula 1.3 expresses how to calculate the net price when multiple discounts apply.

Formula 1.3 – Multiple Discounts

$N=L\times(1-d_1)\times(1-d_2)\times\cdots\times(1-d_n)$

$N$ is Net Price: The dollar amount of the price after all discounts have been deducted.
$L$ is List Price: The dollar amount of the price before any discounts.
$d_1$ is First Discount, $d_2$ is Second Discount, $d_n$ is nth Discount:
When there is more than one discount, you must extend beyond Formula 1.1 by multiplying another discount expression. These discounts are represented by the same d symbol; however, each discount receives a subscript to make its symbol unique. Therefore, the first discount receives the symbol of $d_1$ , the second discount receives the symbol $d_2$ , and so on. Recall that the symbol $n$ represents the number of pieces of data (a count), so you can expand or contract this formula to the exact number of discounts being offered.

It is often difficult to understand exactly how much of a discount is being received when multiple discounts are involved. Often it is convenient to summarize the multiple discount percentages into a single percentage. This makes it easier to calculate the net price and aids in understanding the discount benefit. Simplifying multiple percent discounts into a single percent discount is called finding the single equivalent discount. Whether you apply the multiple discounts or just the single equivalent discount, you arrive at the same net price. The conversion of multiple discount percentages into a single equivalent discount percent is illustrated in Formula 1.4.

Formula 1.4 – Single Equivalent Discount

$d_e_q_u_i_v=1-(1-d_1)\times(1-d_2)\times\cdots\times(1-d_n)$

$d_e_q_u_i_v$ (or just $d$ ) is the single equivalent discount rate that is equal to the series of multiple discounts. Recall that taking $(1-d)$ calculates what you pay. Therefore, if you take 1, which represents the entire amount, and reduce it by what you pay, the rate left over must be what you did not pay. In other words, it is the discount rate.

$d_1$ is First Discount, $d_2$ is Second Discount, $d_n$ is nth Discount:
This is the same notation as in Formula 1.3. Since there are multiple discounts, each discount receives a numerical subscript to give it a unique identifier. You can expand or contract the formula to the exact number of discounts being offered.

How It Works

Refer back to the steps in calculating net price. The procedure for calculating a net price involving a single discount extends to a more generic procedure involving multiple discounts. As with the single discount procedures, you can adapt the model if the net price is known and one of the other variables is unknown. Follow these steps to calculate the net price involving any number of discounts:

Step 1: Identify any known variables, including list price, discount rate(s), or discount amount.

Step 2: If the list price is known, skip this step. Otherwise, solve for list price.

If only one discount is involved, apply Formula 1.2a.
If more than one discount is involved, the discount amount represents the total discount amount received from all of the discounts combined. This requires you first to convert the multiple discount rates into an equivalent single discount rate using Formula 1.4 and then to apply Formula 1.2a.

Step 3: Calculate the net price.

If the list price and only a single known discount rate are involved, apply Formula 1.1.
If the list price and multiple discount rates are known and involved, apply Formula 1.3.
If the list price and the total discount amount are known, apply Formula 1.2b and rearrange for $N$ .

Assume a product with an MSRP of $100 receives a trade discount of 30% and a volume discount of 10%. Calculate the net price.

Step 1: The list price and discounts are

$L = \char36 100$
$d_1 = 0.30$
$d_2 = 0.10$ .

Step 2: List price is known, so skip this step.

Step 3: Apply Formula 1.3 to calculate the net price:

$N=\char36 100\times(1-0.30)\times(1-0.10)=\char36 63$

The net price is $63, which is illustrated in the following diagram:

A circle diagram illustrating pricing with two discounts. The circle represents the MSRP ($100.) The blue portion of the circle illustrates a 30% discount of $100 ($30.) The red portion of the circle illustrates a 10% discount of $70 ($7.) The green portion of the circle illustrates the net price ($63.)

If you are solely interested in converting multiple discounts into a single equivalent discount, you need only substitute into Formula 1.4. In the above example, the product received a trade discount of 30% and a volume discount of 10%. To calculate the single equivalent discount, apply Formula 1.4:

$\begin{array}{r} d_e_q_u_i_v=1-(1-0.30)\times(1-0.10)\\ d_e_q_u_i_v=1-(0.70)(0.90)\\ d_e_q_u_i_v=1-0.63=0.37 \end{array}$

Therefore, whenever discounts of 30% and 10% are offered together, the single equivalent discount is 37%. Whether it is the multiple discounts or just the single equivalent discount that you apply to the list price, the net price calculated is always the same.

Order of Discounts:

The order of the discounts does not matter in determining the net price. Remember from the rules of BEDMAS that you can complete multiplication in any order. Therefore, in the above example you could have arrived at the $63 net price through the following calculation:

$\char36 100\times(1-0.10)\times(1-0.30)=\char36 63$

The order of the discounts does matter if trying to interpret the value of any single discount. If the trade discount is applied before the quantity discount and you are wanting to know the quantity discount amount, then the quantity discount needs to be second. Thus,

$\begin{array}{r} \char36 100\times(1-0.30)=\char36 70\\ \char36 70\times0.10=\char36 7 \end{array}$

which is the amount of the quantity discount.

Price Does Not Affect Single Equivalent Discount:

Notice in Formula 1.4 that the list price and the net price are not involved in the calculation of the single equivalent discount. When working with percentages, whether you have a net price of $6.30 and a list price of $10, or a net price of $63 and a list price of $100, the equivalent percentage always remains constant at 37%.

A common mistake when working with multiple discounts is to add the discounts together to calculate the single equivalent discount. This mistaken single discount is then substituted into Formula 1.1 to arrive at the wrong net price. Remember that if two discounts of 30% and 10% apply, you cannot sum these discounts. The second discount of 10% is applied on a smaller price tag, not the original price tag. To calculate the net price you must apply Formula 1.3.

If you happen to know any two of the net price ( $N$ ), list price ( $L$ ), or the total discount amount ( $D\char36$ ), then you could also use Formula 1.2 to solve for the single equivalent discount, $d_e_q_u_i_v$ .

For example, if you know the net price is $63 and the total discount amount for all discounts is $37, you could use Formula 1.2b to figure out that the list price is $100, then convert the discount amount into a percentage using Formula 1.2a. This method will also produce a single equivalent discount of 37%.

Another method of calculating the single equivalent discount is to recognize Formula 1.2a as an application of Formula 3.1 involving percent change. The variable d is a discount rate, which you interpret as a negative percent change. The discount amount, D, is the difference between the list price (representing the Old price) and the net price (representing the New price after the discount). Therefore, Formula 1.2a can be rewritten as follows:

$D\char36 =L\times d$

becomes

${\textrm{New }}-{\textrm{ Old }}={\textrm{ Old}}\times\Delta\%$

or

$\frac{{\textrm{New }}-{\textrm{ Old}}}{{\textrm{Old}}}=\Delta\%$

Therefore, any question about a single equivalent discount where net price and list price are known can be solved as a percent change. Using our ongoing net price example, you have:

$\begin{array}{r} \frac{\char36 63-\char36 100}{\char36 100}=-0.37 &{\textrm{or }\\ -37\% \end{array}$

This is a discount of 37%.

Give It Some Thought:

3. If you are offered discounts in the amount of 25%, 15%, 10%, and 5%, will your total discount percent be 55%, less than 55%, or more than 55%?

Example 1.1D – Retailer Purchasing Ski-Doos with Multiple Discounts

A retail dealership purchases some Expedition TUV Yeti II Ski-Doos to stock in its stores. Examining the merchandising terms of the manufacturer, Bombardier, the dealership notices that it would be eligible to receive a 35% trade discount, 15% volume discount, and 3% loyalty discount. Because it is June and Ski-Doos are out of season, Bombardier offers a seasonal discount of 12% for purchases made before June 30. If the MSRP for the Ski-Doo is $12,399.00 and the dealership purchases this item on June 15, what price would it pay?

Plan:
You are looking for the net price that the retail dealership will pay for the Ski-Doo, or $N$ .

Understand:
Step 1: The retail dealership is eligible for all four discounts (it qualifies for the seasonal discount since it is purchasing before June 30). Therefore,

$L = \char36 12,399.00$
$d_1 = 0.35$
$d_2 = 0.15$
$d_3 = 0.03$
$d_4 = 0.12$

Step 2: You know the list price, so skip this step.

Step 3: Apply Formula 1.3.

Perform:
Step 3:

$\begin{array}{l} N=\char36 12,399\times(1-0.35)\times(1-0.15)\times(1-0.03)\times(1-0.12)\\ N=\char36 12,399\times0.65\times0.85\times0.97\times0.88=\char36 5,847.54 \end{array}$

Present:
After all four discounts, the retail dealership could purchase the Ski-Doo for $5,847.54.

A circle diagram illustrating Ski-Doo pricing with four discounts. The circle represents the MSRP ($12,399.) The dark blue portion of the circle illustrates a 35% discount of $12,399. ($4,339.65.) The red portion of the circle illustrates a 15% discount of $8,059.45 ($1,208.90.) The green portion of the circle illustrates a 3% discount of $6,850.45 ($205.51.) The purple portion of the circle illustrates a 12% discount of $6,644.93 ($797.39.) The light blue portion of the circle illustrates what you pay after the discounts, or the net price ($5,847.54.) Note that these numbers have been rounded to two decimals for illustrative purposes. In practice, we would need to retain all decimals throughout our calculations.

Example 1.1E – Reducing Multiple Discounts to a Single Equivalent Discount

The retail dealership in Example 1.1D purchases more products subject to the same discounts. It needs to simplify its calculations. Using the information from Example 1.1D, what single equivalent discount is equal to the four specified discounts?

Plan:
You are looking for a single equivalent discount that is equal to the four discount percentages, or $d_e_q_u_i_v$ (or just $d$ ).

Understand:
You know the discount rates:

$d_1 = 0.35$
$d_2 = 0.15$
$d_3 = 0.03$
$d_4 = 0.12$

Apply Formula 1.4.

Perform:

$\begin{array}{r} d_e_q_u_i_v=1-(1-0.35)\times(1-0.15)\times(1-0.03)\times(1-0.12)\\ d_e_q_u_i_v=1-(0.65)(0.85)(0.97)(0.88)\\ d_e_q_u_i_v=1-0.471614=0.528386 &{\textrm{or}\\ 52.8386\% \end{array}$

Present:
The retail dealership can apply a 52.8386% discount to all the products it purchases.

Example 1.1F – Making a Smart Consumer Purchase

You are shopping on Boxing Day for an 80″ HDTV. You have just one credit card in your wallet, a cashback Visa card, which allows for a 1% cash rebate on all purchases. While scanning flyers for the best deal, you notice that Visions is selling the TV for $5,599.99 including taxes, while Best Buy is selling it for $5,571.99 including taxes. However, because of a computer glitch Best Buy is unable to accept Visa today. Where should you buy your television?

Plan:
You want to know which store you should buy the television at. You must calculate the net price (N) for each of the stores.

Understand:
Step 1: You know the list price for each of the stores. You also know the discount available from Visa. Thus,

$L_B_e_s_t_B_u_y = \char36 5,571.99$ with no discounts since Visa cannot be used there
$L_V_i_s_i_o_n_s = \char36 5,599.99$ , $d = 0.01$ , since you can use your Visa card there

Step 2: List price is known, so skip this step.

Step 3: Apply Formula 1.1.

Perform:
Step 3:
Best Buy: No discounts apply, so the list price equals the net price.

$N=\char36 5,571.99$

Visions:

$N=\char36 5,599.99\times(1-0.01)=\char36 5,599.99\times0.99=\char36 5,543.99$

Present:
The net price for Visions is $5,543.99. You save $5,571.99 – $5,543.99 = $28.00 by purchasing your TV at Visions.

Example 1.1G – Understanding the Price

An advertisement claims that at 60% off, you are saving $18. However, today there is an additional 20% off. What price should you pay for this item? What percent savings does this represent?

Plan:
You are looking for how much you should pay after the discounts (N), and the single equivalent percentage that represents the two discounts (d_equiv or just d).

Understand:
Step 1: You know the discount amount for the first discount only, as well as the two discount rates:

$D\char36_1 = \char36 18$
$d_1 = 0.60$
$d_2 = 0.20$

Step 2: Calculate the list price by applying Formula 1.2a and rearranging for L.

Step 3: To calculate the net price, apply Formula 1.3.

Step 4: To calculate the single equivalent discount, apply Formula 1.4.

Perform:
Step 2:

$\begin{array}{r} \char36 18.00=L\times0.60\\ L=\char36 18.00\div0.6=\char36 30.00 \end{array}$

Step 3:

$N=\char36 30\times(1-0.60)\times(1-0.20)=\char36 30\times(0.40)\times(0.80)=\char36 9.60$

Step 4:

$\begin{array}{c} d_e_q_u_i_v=1-(1-0.60)\times(1-0.20)=1-(0.40)(0.80)=1-0.32=0.68 &{\textrm{or}\\ 68\% \end{array}$

Present:
You should pay $9.60 for the item, which represents a 68% savings.

Give It Some Thought Answers

a. Exactly $10. The net price is the price after the discount.
b. Less than $10. The discount needs to be removed from the list price.
More than half. A 40% discount means that you will pay 60% of the list price.

Discount Exercises

Round all money to two decimals and percentages to four decimals in each of the following questions.

Mechanics

For questions 1–4, solve for the unknown variables (identified with a ?) based on the information provided. “N/A” indicates that the particular variable is not applicable in the question.

	List Price or MRSP	First Discount	Second Discount	Third Discount	Net Price	Equivalent Single Discount Rate	Total Discount Amount
1.	$980.00	42%	N/A	N/A	?	N/A	?
2.	?	25%	N/A	N/A	$600.00	N/A	?
3.	$1,975.00	25%	15%	10%	?	?	?
4.	?	18%	4%	7%	$366.05	?	?

Applications

5. A wholesaler of stereos normally qualifies for a 35% trade discount on all electronic products purchased from its manufacturer. If the MSRP of a stereo is $399.95, what net price will the wholesaler pay?

6. Mary is shopping at the mall where she sees a sign that reads, “Everything in the store is 30% off, including sale items!” She wanders in and finds a blouse on the clearance rack. A sign on the clearance rack states, “All clearance items are 50% off.” If the blouse is normally priced at $69.49, what price should Mary pay for it?

7. A distributor sells some shoes directly to a retailer. The retailer pays $16.31 for a pair of shoes that has a list price of $23.98. What trade discount percent is the distributor offering to its retailers?

8. A retailer purchases supplies for its head office. If the retailer pays $16.99 for a box of paper and was eligible for a 15% volume discount, what was the original MSRP for the box of paper?

9. Mountain Equipment Co-op has purchased a college backpack for $29 after discounts of 30%, 8%, and 13%. What is the MSRP for the backpack? What single discount is equivalent to the three discounts?

Check Your Work

Answers can be found in the section titled: Answers for Exercise Questions [11.8]

Attribution
The section on Discounts is reproduced Chapter 4 .1 in Fundamentals of Business Mathematics by OER Lab licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

License

Icon for the Creative Commons Attribution 4.0 International License

Discounts

How Distribution and Pricing Work

Single Discounts

Multiple Discounts

Give It Some Thought Answers

Mechanics

Applications

License

Share This Book