87 Acid-Base Titrations

[latexpage]

Learning Objectives

By the end of this section, you will be able to:

  • Interpret titration curves for strong and weak acid-base systems
  • Compute sample pH at important stages of a titration
  • Explain the function of acid-base indicators

As seen in the chapter on the stoichiometry of chemical reactions, titrations can be used to quantitatively analyze solutions for their acid or base concentrations. In this section, we will explore the underlying chemical equilibria that make acid-base titrimetry a useful analytical technique.

Titration Curves

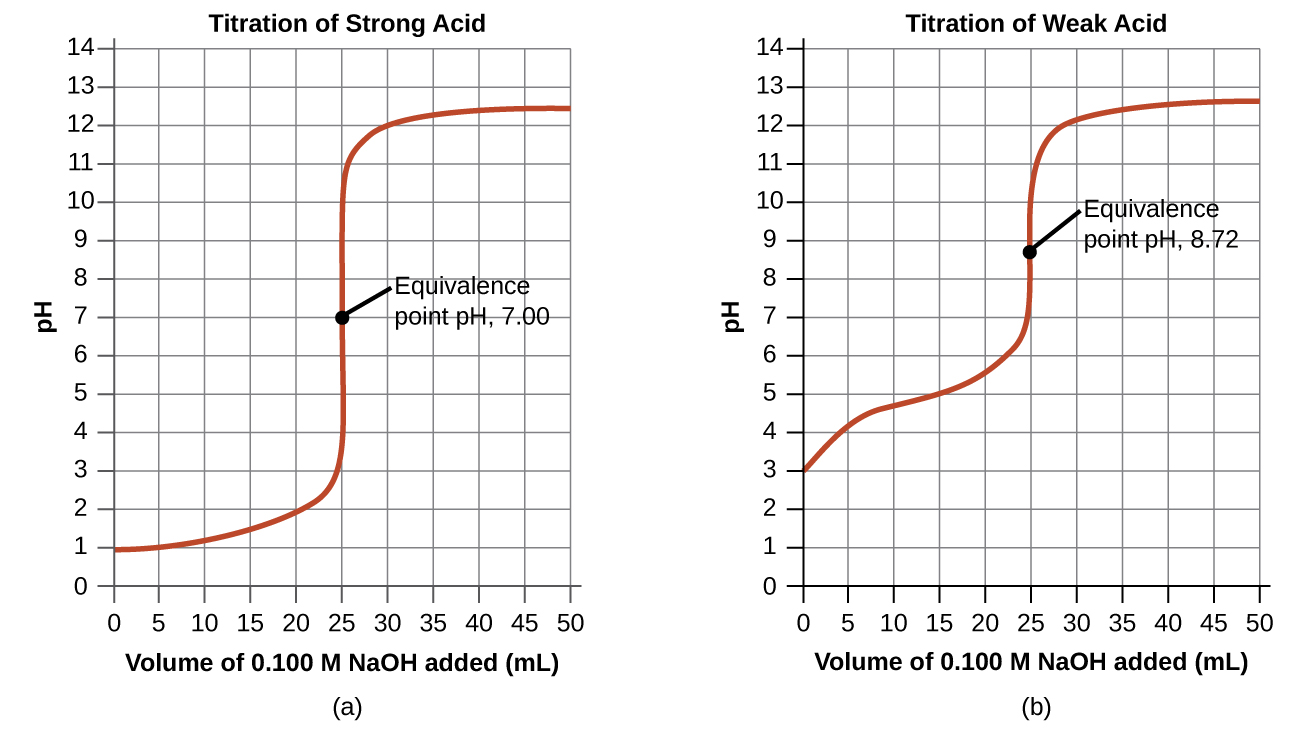
A titration curve is a plot of some solution property versus the amount of added titrant. For acid-base titrations, solution pH is a useful property to monitor because it varies predictably with the solution composition and, therefore, may be used to monitor the titration’s progress and detect its end point. The following example exercise demonstrates the computation of pH for a titration solution after additions of several specified titrant volumes. The first example involves a strong acid titration that requires only stoichiometric calculations to derive the solution pH. The second example addresses a weak acid titration requiring equilibrium calculations.

Calculating pH for Titration Solutions: Strong Acid/Strong Base A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH (the titration curve is shown in (Figure)). Calculate the pH at these volumes of added base solution:

(a) 0.00 mL

(b) 12.50 mL

(c) 25.00 mL

(d) 37.50 mL

Solution (a) Titrant volume = 0 mL. The solution pH is due to the acid ionization of HCl. Because this is a strong acid, the ionization is complete and the hydronium ion molarity is 0.100 M. The pH of the solution is then

\(\text{pH}=-\text{log}\phantom{\rule{0.2em}{0ex}}\left(0.100\right)=1.000\)

(b) Titrant volume = 12.50 mL. Since the acid sample and the base titrant are both monoprotic and equally concentrated, this titrant addition involves less than a stoichiometric amount of base, and so it is completely consumed by reaction with the excess acid in the sample. The concentration of acid remaining is computed by subtracting the consumed amount from the intial amount and then dividing by the solution volume:

\(\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=\phantom{\rule{0.2em}{0ex}}\frac{\text{n}\left({\text{H}}^{\text{+}}\right)}{V}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{\text{0.002500 mol}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(\phantom{\rule{0.2em}{0ex}}\frac{\text{1000 mL}}{\text{1 L}}\right)\phantom{\rule{0.2em}{0ex}}-0.100\phantom{\rule{0.4em}{0ex}}M\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\text{12.50 mL}}{\text{25.00 mL}+\text{12.50 mL}}\phantom{\rule{0.2em}{0ex}}=0.0333\phantom{\rule{0.4em}{0ex}}M\)

(c) Titrant volume = 25.00 mL. This titrant addition involves a stoichiometric amount of base (the equivalence point), and so only products of the neutralization reaction are in solution (water and NaCl). Neither the cation nor the anion of this salt undergo acid-base ionization; the only process generating hydronium ions is the autoprotolysis of water. The solution is neutral, having a pH = 7.00.

(d) Titrant volume = 37.50 mL. This involves the addition of titrant in excess of the equivalence point. The solution pH is then calculated using the concentration of hydroxide ion:

\(\text{n}{\left({\text{OH}}^{\text{−}}\right)}_{0}>\text{n}{\left({\text{H}}^{\text{+}}\right)}_{0}\)
\(\left[{\text{OH}}^{\text{−}}\right]=\phantom{\rule{0.2em}{0ex}}\frac{\text{n}\left({\text{OH}}^{\text{−}}\right)}{V}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{0.100\phantom{\rule{0.4em}{0ex}}M\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\text{35.70 mL}-\text{0.002500 mol}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(\phantom{\rule{0.2em}{0ex}}\frac{\text{1000 mL}}{\text{1 L}}\right)\phantom{\rule{0.2em}{0ex}}}{\text{25.00 mL}+\text{37.50 mL}}\phantom{\rule{0.2em}{0ex}}=0.0200\phantom{\rule{0.4em}{0ex}}M\)

pH = 14 − pOH = 14 + log([OH−]) = 14 + log(0.0200) = 12.30

Check Your Learning Calculate the pH for the strong acid/strong base titration between 50.0 mL of 0.100 M HNO3(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 40.0 mL.

Answer:

0.00: 1.000; 15.0: 1.5111; 25.0: 7; 40.0: 12.523

Titration of a Weak Acid with a Strong Base Consider the titration of 25.00 mL of 0.100 M CH3CO2H with 0.100 M NaOH. The reaction can be represented as:

\({\text{CH}}_{3}{\text{CO}}_{2}\text{H}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CH}}_{3}{\text{CO}}_{2}{}^{\text{−}}+{\text{H}}_{2}\text{O}\)

Calculate the pH of the titration solution after the addition of the following volumes of NaOH titrant:

(a) 0.00 mL

(b) 25.00 mL

(c) 12.50 mL

(d) 37.50 mL

Solution (a) The initial pH is computed for the acetic acid solution in the usual ICE approach:

\({K}_{\text{a}}=\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{\text{−}}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}\phantom{\rule{0.2em}{0ex}}\approx \phantom{\rule{0.2em}{0ex}}\frac{{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}^{\text{2}}}{{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}_{0}}\phantom{\rule{0.2em}{0ex}},\) and \(\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=\sqrt{{K}_{a}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=\sqrt{1.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}0.100}=1.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\)

\(\text{pH}=\text{−log}\left(1.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\right)=2.87\)

(b) The acid and titrant are both monoprotic and the sample and titrant solutions are equally concentrated; thus, this volume of titrant represents the equivalence point. Unlike the strong-acid example above, however, the reaction mixture in this case contains a weak conjugate base (acetate ion). The solution pH is computed considering the base ionization of acetate, which is present at a concentration of

\(\frac{\text{0.00250 mol}}{\text{0.0500 L}}\phantom{\rule{0.2em}{0ex}}=\text{0.0500 M}{\text{CH}}_{3}{\text{CO}}_{2}{}^{\text{−}}\)

Base ionization of acetate is represented by the equation

\({\text{CH}}_{3}{\text{CO}}_{2}{}^{\text{−}}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\)
\({K}_{\text{b}}=\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{H}}^{\text{+}}\right]\left[{\text{OH}}^{\text{−}}\right]}{{K}_{\text{a}}}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{{K}_{\text{w}}}{{K}_{\text{a}}}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}}{1.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}5.6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-10}\)

Assuming x << 0.0500, the pH may be calculated via the usual ICE approach: \({K}_{\text{b}}=\phantom{\rule{0.2em}{0ex}}\frac{{x}^{\text{2}}}{0.0500\phantom{\rule{0.2em}{0ex}}M}\)

\(x=\left[{\text{OH}}^{\text{−}}\right]=5.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\)
\(\text{pOH}=\text{−log}\left(5.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\right)=5.28\)
\(\text{pH}=14.00-5.28=8.72\)

Note that the pH at the equivalence point of this titration is significantly greater than 7, as expected when titrating a weak acid with a strong base.

(c) Titrant volume = 12.50 mL. This volume represents one-half of the stoichiometric amount of titrant, and so one-half of the acetic acid has been neutralized to yield an equivalent amount of acetate ion. The concentrations of these conjugate acid-base partners, therefore, are equal. A convenient approach to computing the pH is use of the Henderson-Hasselbalch equation:

\(\text{pH}=p{K}_{\text{a}}+\text{log}\phantom{\rule{0.2em}{0ex}}\frac{\left[\text{Base}\right]}{\left[\text{Acid}\right]}\phantom{\rule{0.2em}{0ex}}=\text{−log}\left({K}_{\text{a}}\right)+\text{log}\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{\text{−}}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}\phantom{\rule{0.2em}{0ex}}=\text{−log}\left(1.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\right)+\text{log}\left(1\right)\)
\(\text{pH}=\text{−log}\left(1.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\right)=4.74\)

(pH = pKa at the half-equivalence point in a titration of a weak acid)

(d) Titrant volume = 37.50 mL. This volume represents a stoichiometric excess of titrant, and a reaction solution containing both the titration product, acetate ion, and the excess strong titrant. In such solutions, the solution pH is determined primarily by the amount of excess strong base:

\(\left[{\text{OH}}^{\text{−}}\right]=\phantom{\rule{0.2em}{0ex}}\frac{\left(\text{0.003750 mol}-\text{0.00250 mol}\right)}{\text{0.06250 L}}\phantom{\rule{0.2em}{0ex}}=2.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\phantom{\rule{0.2em}{0ex}}M\)
\(\text{pOH}=\text{−log}\left(2.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\right)=\text{1.70, and pH}=14.00-1.70=12.30\)

Check Your Learning Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL.

Answer:

0.00 mL: 2.37; 15.0 mL: 3.92; 25.00 mL: 8.29; 30.0 mL: 12.097

Performing additional calculations similar to those in the preceding example permits a more full assessment of titration curves. A summary of pH/volume data pairs for the strong and weak acid titrations is provided in (Figure) and plotted as titration curves in (Figure). A comparison of these two curves illustrates several important concepts that are best addressed by identifying the four stages of a titration:

initial state (added titrant volume = 0 mL): pH is determined by the acid being titrated; because the two acid samples are equally concentrated, the weak acid will exhibit a greater initial pH

pre-equivalence point (0 mL < V < 25 mL): solution pH increases gradually and the acid is consumed by reaction with added titrant; composition includes unreacted acid and the reaction product, its conjugate base

equivalence point (V = 25 mL): a drastic rise in pH is observed as the solution composition transitions from acidic to either neutral (for the strong acid sample) or basic (for the weak acid sample), with pH determined by ionization of the conjugate base of the acid

postequivalence point (V > 25 mL): pH is determined by the amount of excess strong base titrant added; since both samples are titrated with the same titrant, both titration curves appear similar at this stage.

pH Values in the Titrations of a Strong Acid and of a Weak Acid
Volume of 0.100 M NaOH Added (mL) Moles of NaOH Added pH Values 0.100 M HCl1 pH Values 0.100 M CH3CO2H2
0.0 0.0 1.00 2.87
5.0 0.00050 1.18 4.14
10.0 0.00100 1.37 4.57
15.0 0.00150 1.60 4.92
20.0 0.00200 1.95 5.35
22.0 0.00220 2.20 5.61
24.0 0.00240 2.69 6.13
24.5 0.00245 3.00 6.44
24.9 0.00249 3.70 7.14
25.0 0.00250 7.00 8.72
25.1 0.00251 10.30 10.30
25.5 0.00255 11.00 11.00
26.0 0.00260 11.29 11.29
28.0 0.00280 11.75 11.75
30.0 0.00300 11.96 11.96
35.0 0.00350 12.22 12.22
40.0 0.00400 12.36 12.36
45.0 0.00450 12.46 12.46
50.0 0.00500 12.52 12.52
(a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH. (b) The titration curve for the titration of 25.00 mL of 0.100 M acetic acid (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.

Two graphs are shown. The first graph on the left is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 unis beginning at 0 extending to 14. A red curve is drawn on the graph which increases steadily from the point (0, 3) up to about (20, 5.5) after which the graph has a vertical section from (25, 7) up to (25, 11). The graph then levels off to a value of about 12.5 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.” The second graph on the right is titled “Titration of Strong Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 units beginning at 0 extending to 14. A red curve is drawn on the graph which increases gradually from the point (0, 1) up to about (22.5, 2.2) after which the graph has a vertical section from (25, 4) up to nearly (25, 11). The graph then levels off to a value of about 12.4 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 7.00.”

Acid-Base Indicators

Certain organic substances change color in dilute solution when the hydronium ion concentration reaches a particular value. For example, phenolphthalein is a colorless substance in any aqueous solution with a hydronium ion concentration greater than 5.0 \(×\) 10−9M (pH < 8.3). In more basic solutions where the hydronium ion concentration is less than 5.0 \(×\) 10−9M (pH > 8.3), it is red or pink. Substances such as phenolphthalein, which can be used to determine the pH of a solution, are called acid-base indicators. Acid-base indicators are either weak organic acids or weak organic bases.

The equilibrium in a solution of the acid-base indicator methyl orange, a weak acid, can be represented by an equation in which we use HIn as a simple representation for the complex methyl orange molecule:

\(\begin{array}{ccc}\text{HIn}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)& \phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}& {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{In}}^{\text{−}}\left(aq\right)\\ \phantom{\rule{0.5em}{0ex}}\text{red}\hfill & & \phantom{\rule{5.5em}{0ex}}\text{yellow}\hfill & \end{array}\)
\({K}_{a}=\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{In}}^{\text{−}}\right]}{\left[\text{HIn}\right]}\phantom{\rule{0.2em}{0ex}}=4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\)

The anion of methyl orange, In−, is yellow, and the nonionized form, HIn, is red. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Châtelier’s principle. If we add base, we shift the equilibrium towards the yellow form. This behavior is completely analogous to the action of buffers.

The perceived color of an indicator solution is determined by the ratio of the concentrations of the two species In− and HIn. If most of the indicator (typically about 60−90% or more) is present as In−, the perceived color of the solution is yellow. If most is present as HIn, then the solution color appears red. The Henderson-Hasselbalch equation is useful for understanding the relationship between the pH of an indicator solution and its composition (thus, perceived color):

\(\text{pH}=\text{p}K\text{a}+\text{log}\left(\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{In}}^{\text{−}}\right]}{\left[\text{HIn}\right]}\right)\)

In solutions where pH > pKa, the logarithmic term must be positive, indicating an excess of the conjugate base form of the indicator (yellow solution). When pH > pKa, the log term must be negative, indicating an excess of the conjugate acid (red solution). When the solution pH is close to the indicator pKa, appreciable amounts of both conjugate partners are present, and the solution color is that of an additive combination of each (yellow and red, yielding orange). The color change interval (or pH interval) for an acid-base indicator is defined as the range of pH values over which a change in color is observed, and for most indicators this range is approximately pKa ± 1.

There are many different acid-base indicators that cover a wide range of pH values and can be used to determine the approximate pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pHs. (Figure) presents several indicators, their colors, and their color-change intervals.

This chart illustrates the color change intervals for several acid-base indicators.

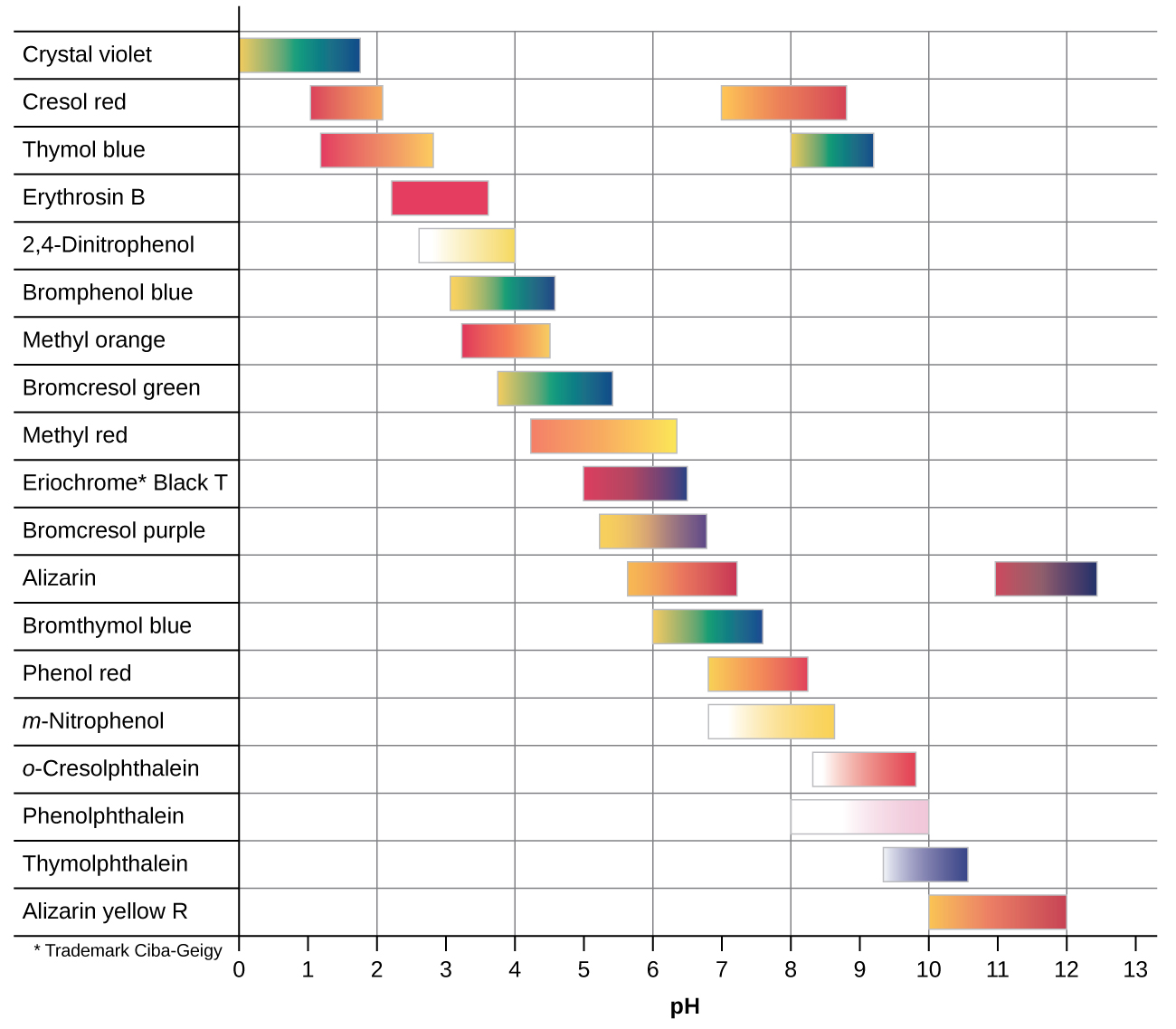
This figure provides a graphical representation of indicators and color ranges. A horizontal axis is labeled “p H.” This axis begins at zero and increases by ones up to 13. The left side of the graphic provides a column with the names of indicators. To the right of each indicator name is either one or two colored bars that are shaded according to the indicator color at various p H ranges. From the top, the first row is labeled “Crystal violet.” The associated colored bar is yellow at its left end at a p H of 0 and changes to green and blue moving right to its endpoint at a p H of 1.8. The second row is labeled “Cresol red.” The associated colored bar is red at its left end at a p H of 1 and changes to orange and yellow moving right to its endpoint at a p H of just over 2. A second bar to its right is yellow at a p H of around 7 and proceeds through orange to red at a p H of about 9. The third row is labeled “Thymol blue.” The associated colored bar is red at its left end at a p H of nearly 1.2 and changes to orange and red moving right to its endpoint at a p H of 2.8. A second bar begins in yellow at a p H of 8 and proceeds through green and blue to its end at a p H of around 9.1. The fourth row is labeled “Erythrosin B.” The associated colored bar is red from a p H of 2.2 to its endpoint at a p H of 3.6. The fifth row is labeled “2 comma 4 dash Dinitrophenol.” The associated colored bar is white at its left end at a p H of 2.6 and changes to yellow at its endpoint at a p H of 4. The sixth row is labeled “Bromophenol blue.” The associated colored bar is yellow at its left end at a p H of 3 and changes to green and blue moving right to its endpoint at a p H of 4.5. The seventh row is labeled “Methyl orange.” The associated colored bar is red-orange at its left end at a p H of 4.2 and changes to yellow moving right to its endpoint at a p H of 6.3. The eighth row is labeled “Bromocresol green.” The associated colored bar is yellow at its left end at a p H of 3.8 and changes to green and blue moving right to its endpoint at a p H of 5.4. The ninth row is labeled “Methyl red.” The associated colored bar is orange at its left end at a p H of 4.2 and changes to yellow moving right to its endpoint at a p H of 6.3. The tenth row is labeled “Eriochrome * Black T.” The associated colored bar is red at its left end at a p H of 5 and changes to purple and blue moving right to its endpoint at a p H of 6.5. The eleventh row is labeled “Bromocresol purple.” The associated colored bar is yellow at its left end at a p H of 5.2 and changes to purple moving right to its endpoint at a p H of 6.8. The twelfth row is labeled “Alizarin.” The first associated colored bar is yellow-orange at its left end at a p H of 5.7 and changes to red moving right to its endpoint at a p H of 7.2. A second bar begins in red at a p H of 11 and changes to purple, then dark blue at its right end at a p H of 12.4. The thirteenth row is labeled “Bromothymol blue.” The associated colored bar is yellow at its left end at a p H of 6 and changes to green and blue moving right to its endpoint at a p H of 7.6. The fourteenth row is labeled “Phenol red.” The associated colored bar is yellow-orange at its left end at a p H of 6.8 and changes to orange and red moving right to its endpoint at a p H of 8.2. The fifteenth row is labeled “m dash Nitrophenol.” The associated colored bar is white at its left end at a p H of 6.8 and changes to yellow moving right to its endpoint at a p H of 8.6. The sixteenth row is labeled “o dash Cresolphthalein.” The associated colored bar is white at its left end at a p H of 8.3 and changes to red moving right to its endpoint at a p H of 9.8. The seventeenth row is labeled “Phenolphthalein.” The associated colored bar is white at its left end at a p H of 8 and changes to pink moving right to its endpoint at a p H of 10. The eighteenth row is labeled “Thymolphthalein.” The associated colored bar is light blue at its left end at a p H of 9.3 and changes to a deep, dark blue moving right to its endpoint at a p H of 10.5. The nineteenth row is labeled “Alizarin yellow R.” The associated colored bar is yellow-orange at its left end at a p H of 10 and changes to red moving right to its endpoint at a p H of 12.

Titration curves for strong and weak acids illustrating the proper choice of acid-base indicator. Any of the three indicators will exhibit a reasonably sharp color change at the equivalence point of the strong acid titration, but only phenolphthalein is suitable for use in the weak acid titration.

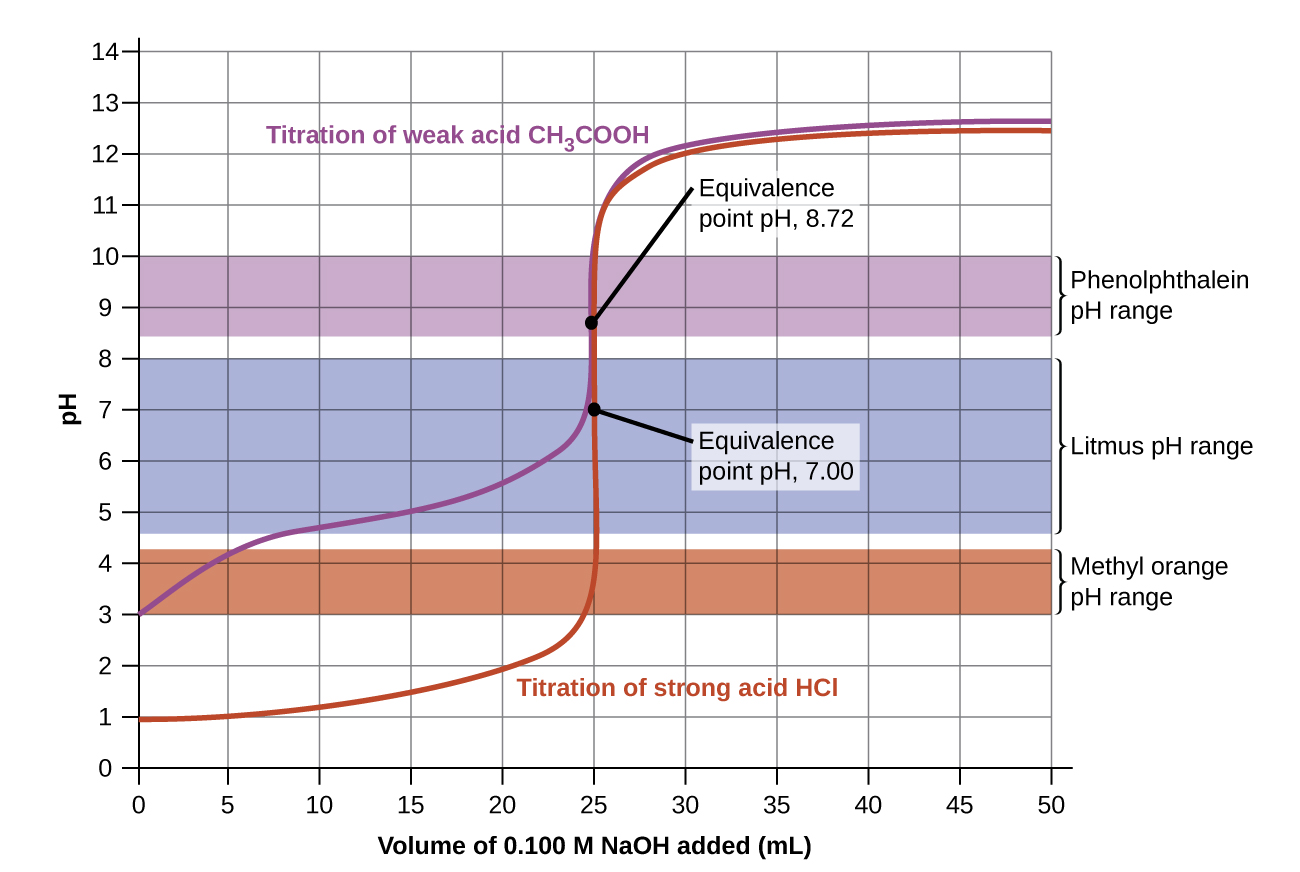
A graph is shown which is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L)” and begins at 0 with markings every 5 units up to 50. The vertical axis is labeled “p H” and begins at 0 and increases by single units up to 14. A red curve is drawn on the graph. The curve begins at (0, 3) and passes through the points (5, 4.1), (10, 4.7), (15, 5), (20, 5.5), and (22.5, 6), after which it rapidly increases, forming a vertical section centered at the point (25, 8.7). The rapid increase of the curve then levels off and the curve passes through the points (30, 12), (35, 12.4), (40, 12.5), (45, 12.6), and (50, 12.6). A brown rectangle extends horizontally across the graph covering the p H of 3 to 4.2 range. To the right, this rectangle is labeled “Methyl orange p H range.” A blue rectangle extends horizontally across the graph covering the p H of 4.6 to 8 range. To the right, this rectangle is labeled “Litmus p H range.” A purple rectangle extends horizontally across the graph covering the p H of 8.4 to 10 range. To the right, this rectangle is labeled “Phenolphthalein p H range.” The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.”

The titration curves shown in (Figure) illustrate the choice of a suitable indicator for specific titrations. In the strong acid titration, use of any of the three indicators should yield reasonably sharp color changes and accurate end point determinations. For this titration, the solution pH reaches the lower limit of the methyl orange color change interval after addition of ~24 mL of titrant, at which point the initially red solution would begin to appear orange. When 25 mL of titrant has been added (the equivalence point), the pH is well above the upper limit and the solution will appear yellow. The titration’s end point may then be estimated as the volume of titrant that yields a distinct orange-to-yellow color change. This color change would be challenging for most human eyes to precisely discern. More-accurate estimates of the titration end point are possible using either litmus or phenolphthalein, both of which exhibit color change intervals that are encompassed by the steep rise in pH that occurs around the 25.00 mL equivalence point.

The weak acid titration curve in (Figure) shows that only one of the three indicators is suitable for end point detection. If methyl orange is used in this titration, the solution will undergo a gradual red-to-orange-to-yellow color change over a relatively large volume interval (0–6 mL), completing the color change well before the equivalence point (25 mL) has been reached. Use of litmus would show a color change that begins after adding 7–8 mL of titrant and ends just before the equivalence point. Phenolphthalein, on the other hand, exhibits a color change interval that nicely brackets the abrupt change in pH occurring at the titration’s equivalence point. A sharp color change from colorless to pink will be observed within a very small volume interval around the equivalence point.

Key Concepts and Summary

The titration curve for an acid-base titration is typically a plot of pH versus volume of added titrant. These curves are useful in selecting appropriate acid-base indicators that will permit accurate determinations of titration end points.

Explain how to choose the appropriate acid-base indicator for the titration of a weak base with a strong acid.

At the equivalence point in the titration of a weak base with a strong acid, the resulting solution is slightly acidic due to the presence of the conjugate acid. Thus, pick an indicator that changes color in the acidic range and brackets the pH at the equivalence point. Methyl orange is a good example.

Explain why an acid-base indicator changes color over a range of pH values rather than at a specific pH.

Calculate the pH at the following points in a titration of 40 mL (0.040 L) of 0.100 M barbituric acid (Ka = 9.8 \(×\) 10−5) with 0.100 M KOH.

(a) no KOH added

(b) 20 mL of KOH solution added

(c) 39 mL of KOH solution added

(d) 40 mL of KOH solution added

(e) 41 mL of KOH solution added

(a) pH = 2.50; (b) pH = 4.01; (c) pH = 5.60; (d) pH = 8.35; (e) pH = 11.08

The indicator dinitrophenol is an acid with a Ka of 1.1 \(×\) 10−4. In a 1.0 \(×\) 10−4–M solution, it is colorless in acid and yellow in base. Calculate the pH range over which it goes from 10% ionized (colorless) to 90% ionized (yellow).

Footnotes

  • 1Titration of 25.00 mL of 0.100 M HCl (0.00250 mol of HCI) with 0.100 M NaOH.
  • 2Titration of 25.00 mL of 0.100 M CH3CO2H (0.00250 mol of CH3CO2H) with 0.100 M NaOH.

Glossary

acid-base indicator
weak acid or base whose conjugate partner imparts a different solution color; used in visual assessments of solution pH
color-change interval
range in pH over which the color change of an indicator is observed
titration curve
plot of some sample property (such as pH) versus volume of added titrant

License

Icon for the Creative Commons Attribution 4.0 International License

Atoms First / OpenStax Copyright © 2018 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book