81 Brønsted-Lowry Acids and Bases

[latexpage]

Learning Objectives

By the end of this section, you will be able to:

  • Identify acids, bases, and conjugate acid-base pairs according to the Brønsted-Lowry definition
  • Write equations for acid and base ionization reactions
  • Use the ion-product constant for water to calculate hydronium and hydroxide ion concentrations
  • Describe the acid-base behavior of amphiprotic substances

The acid-base reaction class has been studied for quite some time. In 1680, Robert Boyle reported traits of acid solutions that included their ability to dissolve many substances, to change the colors of certain natural dyes, and to lose these traits after coming in contact with alkali (base) solutions. In the eighteenth century, it was recognized that acids have a sour taste, react with limestone to liberate a gaseous substance (now known to be CO2), and interact with alkalis to form neutral substances. In 1815, Humphry Davy contributed greatly to the development of the modern acid-base concept by demonstrating that hydrogen is the essential constituent of acids. Around that same time, Joseph Louis Gay-Lussac concluded that acids are substances that can neutralize bases and that these two classes of substances can be defined only in terms of each other. The significance of hydrogen was reemphasized in 1884 when Svante Arrhenius defined an acid as a compound that dissolves in water to yield hydrogen cations (now recognized to be hydronium ions) and a base as a compound that dissolves in water to yield hydroxide anions.

Johannes Brønsted and Thomas Lowry proposed a more general description in 1923 in which acids and bases were defined in terms of the transfer of hydrogen ions, H+. (Note that these hydrogen ions are often referred to simply as protons, since that subatomic particle is the only component of cations derived from the most abundant hydrogen isotope, 1H.) A compound that donates a proton to another compound is called a Brønsted-Lowry acid, and a compound that accepts a proton is called a Brønsted-Lowry base. An acid-base reaction is, thus, the transfer of a proton from a donor (acid) to an acceptor (base).

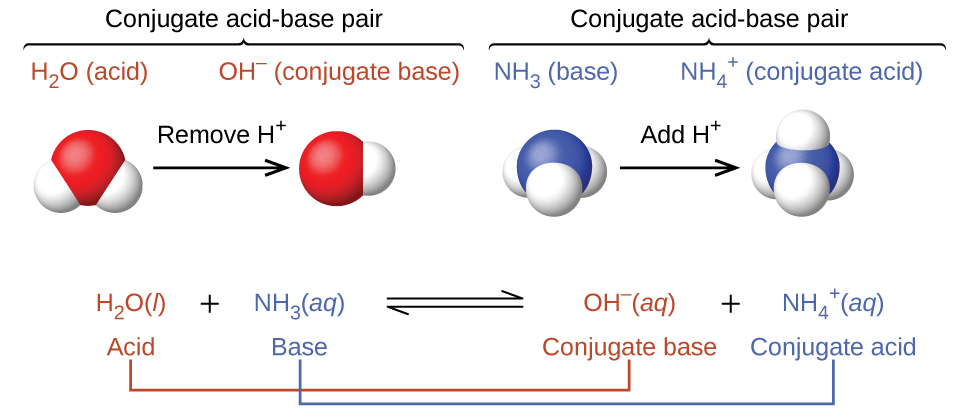
The concept of conjugate pairs is useful in describing Brønsted-Lowry acid-base reactions (and other reversible reactions, as well). When an acid donates H+, the species that remains is called the conjugate base of the acid because it reacts as a proton acceptor in the reverse reaction. Likewise, when a base accepts H+, it is converted to its conjugate acid. The reaction between water and ammonia illustrates this idea. In the forward direction, water acts as an acid by donating a proton to ammonia and subsequently becoming a hydroxide ion, OH−, the conjugate base of water. The ammonia acts as a base in accepting this proton, becoming an ammonium ion, \({{\text{NH}}_{4}}^{\text{+}}\text{,}\) the conjugate acid of ammonia. In the reverse direction, a hydroxide ion acts as a base in accepting a proton from ammonium ion, which acts as an acid.

This figure has two rows. In both rows, a chemical reaction is shown. In the first, structural formulas are provided. In this model, in red, an H atom is connected to an F atom with a single bond. The F atom has pairs of electron dots at the top, right, and bottom. This is followed by a plus sign, which is followed in blue by an O atom which has H atoms singly bonded above and to the right. The O atom has pairs of electron dots on its left and lower sides. A double arrow follows. To the right, in brackets is a structure with a central O atom in blue, with blue H atoms singly bonded above and to the right. A pair of blue electron dots is on the lower side of the O atom. To the left of the blue O atom, a red H atom is singly bonded. This is followed by a plus sign and an F atom in red with pairs of electron dots above, right, below, and to the left. This atom also has a superscript negative sign. The reaction is written in symbolic form below. H F is labeled in red below as “Acid.” This is followed by plus H subscript 2 O, which is labeled in blue below as “Base.” A double sided arrow follows. To the right is H subscript 3 O superscript plus, which is labeled in blue below as “Acid.” This is followed by plus and F superscript negative. The label below in red reads, “Base.”

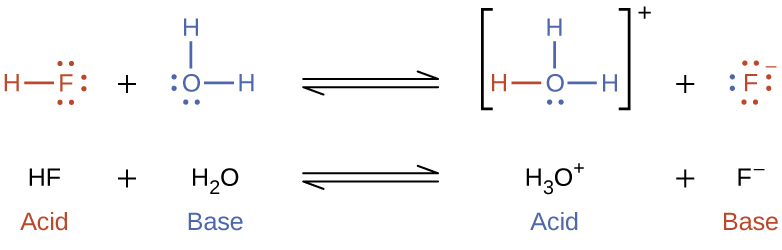
The reaction between a Brønsted-Lowry acid and water is called acid ionization. For example, when hydrogen fluoride dissolves in water and ionizes, protons are transferred from hydrogen fluoride molecules to water molecules, yielding hydronium ions and fluoride ions:

This figure has two rows. In both rows, a chemical reaction is shown. In the first, structural formulas are provided. In this model, in red, is an O atom which has H atoms singly bonded above and to the right. The O atom has lone pairs of electron dots on its left and lower sides. This is followed by a plus sign. The plus sign is followed, in blue, by an N atom with one lone pair of electron dots. The N atom forms a double bond with a C atom, which forms a single bond with a C atom. The second C atom forms a double bond with another C atom, which forms a single bond with another C atom. The fourth C atom forms a double bond with a fifth C atom, which forms a single bond with the N atom. This creates a ring structure. Each C atom is also bonded to an H atom. An equilibrium arrow follows this structure. To the right, in brackets is a structure where an N atom bonded to an H atom, which is red, appears. The N atom forms a double bond with a C atom, which forms a single bond with a C atom. The second C atom forms a double bond with another C atom, which forms a single bond with another C atom. The fourth C atom forms a double bond with a fifth C atom, which forms a single bond with the N atom. This creates a ring structure. Each C atom is also bonded to an H atom. Outside the brackets, to the right, is a superscript positive sign. This structure is followed by a plus sign. Another structure that appears in brackets also appears. An O atom with three lone pairs of electron dots is bonded to an H atom. There is a superscript negative sign outside the brackets. Under the initial equation, is this equation: H subscript 2 plus C subscript 5 N H subscript 5 equilibrium arrow C subscript 5 N H subscript 6 superscript positive sign plus O H superscript negative sign. H subscript 2 O is labeled, “acid,” in red. C subscript 5 N H subscript 5 is labeled, “base,” in blue. C subscript 5 N H subscript 6 superscript positive sign is labeled, “acid” in blue. O H superscript negative sign is labeled, “base,” in red.

Base ionization of a species occurs when it accepts protons from water molecules. In the example below, pyridine molecules, C5NH5, undergo base ionization when dissolved in water, yielding hydroxide and pyridinium ions:

This figure has two rows. In both rows, a chemical reaction is shown. In the first, structural formulas are provided. In this model, in red, is an O atom which has H atoms singly bonded above and to the right. The O atom has lone pairs of electron dots on its left and lower sides. This is followed by a plus sign. The plus sign is followed, in blue, by an N atom with one lone pair of electron dots. The N atom forms a double bond with a C atom, which forms a single bond with a C atom. The second C atom forms a double bond with another C atom, which forms a single bond with another C atom. The fourth C atom forms a double bond with a fifth C atom, which forms a single bond with the N atom. This creates a ring structure. Each C atom is also bonded to an H atom. An equilibrium arrow follows this structure. To the right, in brackets is a structure where an N atom bonded to an H atom, which is red, appears. The N atom forms a double bond with a C atom, which forms a single bond with a C atom. The second C atom forms a double bond with another C atom, which forms a single bond with another C atom. The fourth C atom forms a double bond with a fifth C atom, which forms a single bond with the N atom. This creates a ring structure. Each C atom is also bonded to an H atom. Outside the brackets, to the right, is a superscript positive sign. This structure is followed by a plus sign. Another structure that appears in brackets also appears. An O atom with three lone pairs of electron dots is bonded to an H atom. There is a superscript negative sign outside the brackets. To the right, is the equation: k equals [ C subscript 5 N H subscript 6 superscript positive sign ] [ O H superscript negative sign] all divided by [ C subscript 5 N H subscript 5 ]. Under the initial equation, is this equation: H subscript 2 plus C subscript 5 N H subscript 5 equilibrium arrow C subscript 5 N H subscript 6 superscript positive sign plus O H superscript negative sign. H subscript 2 O is labeled, “acid,” in red. C subscript 5 N H subscript 5 is labeled, “base,” in blue. C subscript 5 N H subscript 6 superscript positive sign is labeled, “acid” in blue. O H superscript negative sign is labeled, “base,” in red.

The preceding ionization reactions suggest that water may function as both a base (as in its reaction with hydrogen fluoride) and an acid (as in its reaction with ammonia). Species capable of either donating or accepting protons are called amphiprotric, or more generally, amphoteric, a term that may be used for acids and bases per definitions other than the Brønsted-Lowry one. The equations below show the two possible acid-base reactions for two amphiprotic species, bicarbonate ion and water:

\({\text{HCO}}_{3}{}^{–}\left(\text{aq}\right)+{\text{H}}_{2}\text{O}\left(\text{l}\right)\phantom{\rule{4em}{0ex}}{\text{CO}}_{3}{}^{2–}\left(\text{aq}\right)+{\text{H}}_{3}{\text{O}}^{+}\left(\text{aq}\right)\)
\({\text{HCO}}_{3}{}^{–}\left(\text{aq}\right)+{\text{H}}_{2}\text{O}\left(\text{l}\right)\phantom{\rule{4em}{0ex}}{\text{H}}_{2}{\text{CO}}_{3}\left(\text{aq}\right)+{\text{OH}}^{–}\left(\text{aq}\right)\)

The first equation represents the reaction of bicarbonate as an acid with water as a base, whereas the second represents reaction of bicarbonate as a base with water as an acid. When bicarbonate is added to water, both these equilibria are established simultaneously and the composition of the resulting solution may be determined through appropriate equilibrium calculations, as described later in this chapter.

In the liquid state, molecules of an amphiprotic substance can react with one another as illustrated for water in the equations below:

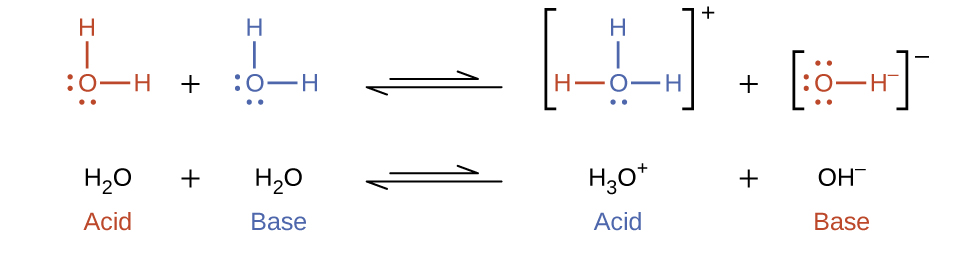
This figure has two rows. In both rows, a chemical reaction is shown. In the first, structural formulas are provided. In this model, in purple, O atom which has H atoms singly bonded above and to the right. The O atom has pairs of electron dots on its left and lower sides. This is followed by a plus sign, which is followed in green by an O atom which has H atoms singly bonded above and to the right. The O atom has pairs of electron dots on its left and lower sides. A double arrow follows. To the right, in brackets is a structure with a central O atom in green, with green H atoms singly bonded above and to the right. A pair of green electron dots is on the lower side of the O atom. To the left of the green O atom, a purple H atom is singly bonded. Outside the brackets to the right is a superscript plus. This is followed by a plus sign and an O atom in purple with pairs of electron dots above, left, and below. An H atom is singly bonded to the right. This atom has a superscript negative sign. The reaction is written in symbolic form below. H subscript 2 O is labeled in purple below as “Acid subscript 1.” This is followed by plus H subscript 2 O, which is labeled in green below as “Base subscript 2.” A double sided arrow follows. To the right is H subscript 3 O superscript plus, which is labeled in green as below in as “Acid subscript 2.” This is followed by plus and O with pairs of dots above, below, and to the left with a singly bonded H on the right with a superscript negative. The label below in purple reads, “ Base subscript 1.”

The process in which like molecules react to yield ions is called autoionization. Liquid water undergoes autoionization to a very slight extent; at 25 °C, approximately two out of every billion water molecules are ionized. The extent of the water autoionization process is reflected in the value of its equilibrium constant, the ion-product constant for water, Kw:

\({\text{H}}_{2}\text{O}\left(l\right)+{\text{H}}_{2}\text{O}\left(l\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\phantom{\rule{5em}{0ex}}{K}_{\text{w}}=\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{OH}}^{\text{−}}\right]\)

The slight ionization of pure water is reflected in the small value of the equilibrium constant; at 25 °C, Kw has a value of 1.0 \(×\) 10−14. The process is endothermic, and so the extent of ionization and the resulting concentrations of hydronium ion and hydroxide ion increase with temperature. For example, at 100 °C, the value for Kw is about 5.6 \(×\) 10−13, roughly 50 times larger than the value at 25 °C.

Ion Concentrations in Pure Water What are the hydronium ion concentration and the hydroxide ion concentration in pure water at 25 °C?

Solution The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, [H3O+] = [OH−] = x. At 25 °C:

\({K}_{\text{w}}=\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{OH}}^{\text{−}}\right]=x=1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}\)

So:

\(x=\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=\left[{\text{OH}}^{\text{−}}\right]=\sqrt{1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}}=1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}M\)

The hydronium ion concentration and the hydroxide ion concentration are the same, 1.0 \(×\) 10−7M.

Check Your Learning The ion product of water at 80 °C is 2.4 \(×\) 10−13. What are the concentrations of hydronium and hydroxide ions in pure water at 80 °C?

Answer:

[H3O+] = [OH−] = 4.9 \(×\) 10−7M

The Inverse Relation between [H3O+] and [OH−] A solution of an acid in water has a hydronium ion concentration of 2.0 \(×\) 10−6M. What is the concentration of hydroxide ion at 25 °C?

Solution Use the value of the ion-product constant for water at 25 °C

\(2{\text{H}}_{2}\text{O}\left(l\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\phantom{\rule{5em}{0ex}}{K}_{\text{w}}=\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{OH}}^{\text{−}}\right]=1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}\)

to calculate the missing equilibrium concentration.

Rearrangement of the Kw expression shows that [OH−] is inversely proportional to [H3O+]:

\(\left[{\text{OH}}^{\text{−}}\right]=\phantom{\rule{0.2em}{0ex}}\frac{{K}_{\text{w}}}{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}}{2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}}\phantom{\rule{0.2em}{0ex}}=5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\)

Compared with pure water, a solution of acid exhibits a higher concentration of hydronium ions (due to ionization of the acid) and a proportionally lower concentration of hydroxide ions. This may be explained via Le Châtelier’s principle as a left shift in the water autoionization equilibrium resulting from the stress of increased hydronium ion concentration.

Substituting the ion concentrations into the Kw expression confirms this calculation, resulting in the expected value:

\({K}_{\text{w}}=\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{OH}}^{\text{−}}\right]=\left(2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\right)\left(5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\right)=1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}\)

Check Your Learning What is the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C?

Answer:

[H3O+] = 1 \(×\) 10−11M

Representing the Acid-Base Behavior of an Amphoteric Substance Write separate equations representing the reaction of \({\text{HSO}}_{3}{}^{\text{−}}\)

(a) as an acid with OH−

(b) as a base with HI

Solution (a) \({\text{HSO}}_{3}{}^{\text{−}}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{SO}}_{3}{}^{\text{2−}}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\)

(b) \({\text{HSO}}_{3}{}^{\text{−}}\left(aq\right)+\text{HI}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}{\text{SO}}_{3}\left(aq\right)+{\text{I}}^{\text{−}}\left(aq\right)\)

Check Your Learning Write separate equations representing the reaction of \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\)

(a) as a base with HBr

(b) as an acid with OH−

Answer:

(a) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\left(aq\right)+\text{HBr}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{PO}}_{4}\left(aq\right)+{\text{Br}}^{\text{−}}\left(aq\right);\) (b) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{HPO}}_{4}{}^{\text{2−}}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\)

Key Concepts and Summary

A compound that can donate a proton (a hydrogen ion) to another compound is called a Brønsted-Lowry acid. The compound that accepts the proton is called a Brønsted-Lowry base. The species remaining after a Brønsted-Lowry acid has lost a proton is the conjugate base of the acid. The species formed when a Brønsted-Lowry base gains a proton is the conjugate acid of the base. Thus, an acid-base reaction occurs when a proton is transferred from an acid to a base, with formation of the conjugate base of the reactant acid and formation of the conjugate acid of the reactant base. Amphiprotic species can act as both proton donors and proton acceptors. Water is the most important amphiprotic species. It can form both the hydronium ion, H3O+, and the hydroxide ion, OH− when it undergoes autoionization:

\({\text{2H}}_{2}\text{O(}l\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\)

The ion product of water, Kw is the equilibrium constant for the autoionization reaction:

\({K}_{\text{w}}=\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{OH}}^{\text{−}}\right]=1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}1{0}^{-14}\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}25\phantom{\rule{0.2em}{0ex}}\text{°C}\)

Key Equations

  • Kw = [H3O+][OH−] = 1.0 \(×\) 10−14 (at 25 °C)

Chemistry End of Chapter Exercises

Write equations that show NH3 as both a conjugate acid and a conjugate base.

One example for NH3 as a conjugate acid: \({\text{NH}}_{2}{}^{\text{−}}+{\text{H}}^{\text{+}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NH}}_{3};\) as a conjugate base: \({\text{NH}}_{4}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\)

Write equations that show \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\) acting both as an acid and as a base.

Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry acid:

(a) \({\text{H}}_{3}{\text{O}}^{\text{+}}\)

(b) HCl

(c) NH3

(d) CH3CO2H

(e) \({\text{NH}}_{4}{}^{\text{+}}\)

(f) \({\text{HSO}}_{4}{}^{\text{−}}\)

(a) \({\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{\text{+}}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right);\) (b) \(\text{HCl}\left(\mathrm{aq}\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{\text{+}}\left(aq\right)+{\text{Cl}}^{\text{−}}\left(aq\right);\) (c) \({\text{NH}}_{3}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{\text{+}}\left(aq\right)+{\text{NH}}_{2}{}^{\text{−}}\left(aq\right);\) (d) \({\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{\text{−}}\left(aq\right);\) (e) \({\text{NH}}_{4}{}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{\text{+}}\left(aq\right)+{\text{NH}}_{3}\left(aq\right);\) (f) \({\text{HSO}}_{4}{}^{\text{−}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{+}\left(aq\right)+{\text{SO}}_{4}{}^{\text{2−}}\left(aq\right)\)

Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry acid:

(a) HNO3

(b) \({\text{PH}}_{4}{}^{\text{+}}\)

(c) H2S

(d) CH3CH2COOH

(e) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\)

(f) HS−

Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry base:

(a) H2O

(b) OH−

(c) NH3

(d) CN−

(e) S2−

(f) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\)

(a) \({\text{H}}_{2}\text{O}\left(l\right)+{\text{H}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right);\) (b) \({\text{OH}}^{\text{−}}\left(aq\right)+{\text{H}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}\text{O}\left(l\right);\) (c) \({\text{NH}}_{3}\left(aq\right)+{\text{H}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NH}}_{4}{}^{\text{+}}\left(aq\right);\) (d) \({\text{CN}}^{\text{−}}\left(aq\right)+{\text{H}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{HCN}\left(aq\right);\) (e) \({\text{S}}^{2-}\left(aq\right)+{\text{H}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{HS}}^{\text{−}}\left(aq\right);\) (f) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\left(aq\right)+{\text{H}}^{\text{+}}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{PO}}_{4}\left(aq\right)\)

Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry base:

(a) HS−

(b) \({\text{PO}}_{4}{}^{\text{3−}}\)

(c) \({\text{NH}}_{2}{}^{\text{−}}\)

(d) C2H5OH

(e) O2−

(f) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\)

What is the conjugate acid of each of the following? What is the conjugate base of each?

(a) OH−

(b) H2O

(c) \({\text{HCO}}_{3}{}^{\text{−}}\)

(d) NH3

(e) \({\text{HSO}}_{4}{}^{\text{−}}\)

(f) H2O2

(g) HS−

(h) \({\text{H}}_{5}{\text{N}}_{2}{}^{\text{+}}\)

(a) H2O, O2−; (b) H3O+, OH−; (c) H2CO3, \({\text{CO}}_{3}{}^{\text{2−}};\) (d) \({\text{NH}}_{4}{}^{\text{+}},\) \({\text{NH}}_{2}{}^{\text{−}};\) (e) H2SO4, \({\text{SO}}_{4}{}^{\text{2−}};\) (f) \({\text{H}}_{3}{\text{O}}_{2}{}^{\text{+}},\) \({\text{HO}}_{2}{}^{\text{−}};\) (g) H2S; S2−; (h) \({\text{H}}_{6}{\text{N}}_{2}{}^{2+},\) H4N2

What is the conjugate acid of each of the following? What is the conjugate base of each?

(a) H2S

(b) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\)

(c) PH3

(d) HS−

(e) \({\text{HSO}}_{3}{}^{\text{−}}\)

(f) \({\text{H}}_{3}{\text{O}}_{2}{}^{\text{+}}\)

(g) H4N2

(h) CH3OH

Identify and label the Brønsted-Lowry acid, its conjugate base, the Brønsted-Lowry base, and its conjugate acid in each of the following equations:

(a) \({\text{HNO}}_{3}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{\text{+}}+{\text{NO}}_{3}{}^{\text{−}}\)

(b) \({\text{CN}}^{\text{−}}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{HCN}+{\text{OH}}^{\text{−}}\)

(c) \({\text{H}}_{2}{\text{SO}}_{4}+{\text{Cl}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{HCl}+{\text{HSO}}_{4}{}^{\text{−}}\)

(d) \({\text{HSO}}_{4}{}^{\text{−}}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{SO}}_{4}{}^{\text{2−}}+{\text{H}}_{2}\text{O}\)

(e) \({\text{O}}^{2-}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}2{\mathrm{OH}}^{\text{−}}\)

(f) \({\left[\text{Cu}{\left({\text{H}}_{2}\text{O}\right)}_{3}\left(\text{OH}\right)\right]}^{\text{+}}+{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{6}\right]}^{3+}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\left[\text{Cu}{\left({\text{H}}_{2}\text{O}\right)}_{4}\right]}^{2+}+{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{5}\left(\text{OH}\right)\right]}^{2+}\)

(g) \({\text{H}}_{2}\text{S}+{\text{NH}}_{2}{}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{HS}}^{\text{−}}+{\text{NH}}_{3}\)

The labels are Brønsted-Lowry acid = BA; its conjugate base = CB; Brønsted-Lowry base = BB; its conjugate acid = CA. (a) HNO3(BA), H2O(BB), H3O+(CA), \({\text{NO}}_{3}{}^{\text{−}}\left(\text{CB}\right);\) (b) CN−(BB), H2O(BA), HCN(CA), OH−(CB); (c) H2SO4(BA), Cl−(BB), HCl(CA), \({\text{HSO}}_{4}{}^{\text{−}}\left(\text{CB}\right);\) (d) \({\text{HSO}}_{4}{}^{\text{−}}\left(\text{BA}\right),\) OH−(BB), \({\text{SO}}_{4}{}^{\text{2−}}\)(CB), H2O(CA); (e) O2−(BB), H2O(BA) OH−(CB and CA); (f) [Cu(H2O)3(OH)]+(BB), [Al(H2O)6]3+(BA), [Cu(H2O)4]2+(CA), [Al(H2O)5(OH)]2+(CB); (g) H2S(BA), \({\text{NH}}_{2}{}^{\text{−}}\left(\text{BB}\right),\) HS−(CB), NH3(CA)

Identify and label the Brønsted-Lowry acid, its conjugate base, the Brønsted-Lowry base, and its conjugate acid in each of the following equations:

(a) \({\text{NO}}_{2}{}^{\text{−}}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{HNO}}_{2}+{\text{OH}}^{\text{−}}\)

(b) \(\text{HBr}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{\text{+}}+{\text{Br}}^{\text{−}}\)

(c) \({\text{HS}}^{\text{−}}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}\text{S}+{\text{OH}}^{\text{−}}\)

(d) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{HPO}}_{4}{}^{\text{2−}}+{\text{H}}_{2}\text{O}\)

(e) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}+\text{HCl}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{PO}}_{4}+{\text{Cl}}^{\text{−}}\)

(f) \({\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{5}\left(\text{OH}\right)\right]}^{2+}+{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{6}\right]}^{3+}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{[Fe}{\left({\text{H}}_{2}\text{O}\right)}_{6}\right]}^{3+}+{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{5}\left(\text{OH}\right)\right]}^{2+}\)

(g) \({\text{CH}}_{3}\text{OH}+{\text{H}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CH}}_{3}{\text{O}}^{\text{−}}+{\text{H}}_{2}\)

What are amphiprotic species? Illustrate with suitable equations.

Amphiprotic species may either gain or lose a proton in a chemical reaction, thus acting as a base or an acid. An example is H2O. As an acid: \({\text{H}}_{2}\text{O}\left(aq\right)+{\text{NH}}_{3}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{NH}}_{4}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{\text{−}}\left(aq\right).\) As a base: \({\text{H}}_{2}\text{O}\left(aq\right)+\text{HCl}\left(aq\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{Cl}}^{\text{−}}\left(aq\right)\)

State which of the following species are amphiprotic and write chemical equations illustrating the amphiprotic character of these species:

(a) H2O

(b) \({\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}\)

(c) S2−

(d) \({\text{CO}}_{3}{}^{\text{2−}}\)

(e) \({\text{HSO}}_{4}{}^{\text{−}}\)

State which of the following species are amphiprotic and write chemical equations illustrating the amphiprotic character of these species.

(a) NH3

(b) \({\text{HPO}}_{4}{}^{\text{−}}\)

(c) Br−

(d) \({\text{NH}}_{4}{}^{\text{+}}\)

(e) \({\text{ASO}}_{4}{}^{\text{3−}}\)

amphiprotic: (a) \({\text{NH}}_{3}+{\text{H}}_{3}{\text{O}}^{\text{+}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NH}}_{4}\text{OH}+{\text{H}}_{2}\text{O},\) \({\text{NH}}_{3}+{\text{OCH}}_{3}{}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NH}}_{2}{}^{\text{−}}+{\text{CH}}_{3}\text{OH};\) (b) \({\text{HPO}}_{4}{}^{\text{2−}}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{PO}}_{4}{}^{\text{3−}}+{\text{H}}_{2}\text{O},\) \({\text{HPO}}_{4}{}^{\text{2−}}+{\text{HClO}}_{4}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}{\text{PO}}_{4}{}^{\text{−}}+{\text{ClO}}_{4}{}^{\text{−}};\) not amphiprotic: (c) Br−; (d) \({\text{NH}}_{4}{}^{\text{+}};\) (e) \({\text{AsO}}_{4}{}^{\text{3−}}\)

Is the self-ionization of water endothermic or exothermic? The ionization constant for water (Kw) is 2.9 \(×\) 10−14 at 40 °C and 9.3 \(×\) 10−14 at 60 °C.

Glossary

acid ionization
reaction involving the transfer of a proton from an acid to water, yielding hydronium ions and the conjugate base of the acid
amphiprotic
species that may either donate or accept a proton in a Bronsted-Lowry acid-base reaction
amphoteric
species that can act as either an acid or a base
autoionization
reaction between identical species yielding ionic products; for water, this reaction involves transfer of protons to yield hydronium and hydroxide ions
base ionization
reaction involving the transfer of a proton from water to a base, yielding hydroxide ions and the conjugate acid of the base
Brønsted-Lowry acid
proton donor
Brønsted-Lowry base
proton acceptor
conjugate acid
substance formed when a base gains a proton
conjugate base
substance formed when an acid loses a proton
ion-product constant for water (Kw)
equilibrium constant for the autoionization of water

License

Icon for the Creative Commons Attribution 4.0 International License

Atoms First / OpenStax Copyright © 2018 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book