107 Catalysis

[latexpage]

Learning Objectives

By the end of this section, you will be able to:

  • Explain the function of a catalyst in terms of reaction mechanisms and potential energy diagrams
  • List examples of catalysis in natural and industrial processes

Catalysts Do Not Affect Equilibrium

A catalyst can speed up the rate of a reaction. Though this increase in reaction rate may cause a system to reach equilibrium more quickly (by speeding up the forward and reverse reactions), a catalyst has no effect on the value of an equilibrium constant nor on equilibrium concentrations.

The interplay of changes in concentration or pressure, temperature, and the lack of an influence of a catalyst on a chemical equilibrium is illustrated in the industrial synthesis of ammonia from nitrogen and hydrogen according to the equation

\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\)

A large quantity of ammonia is manufactured by this reaction. Each year, ammonia is among the top 10 chemicals, by mass, manufactured in the world. About 2 billion pounds are manufactured in the United States each year.

Ammonia plays a vital role in our global economy. It is used in the production of fertilizers and is, itself, an important fertilizer for the growth of corn, cotton, and other crops. Large quantities of ammonia are converted to nitric acid, which plays an important role in the production of fertilizers, explosives, plastics, dyes, and fibers, and is also used in the steel industry.

Fritz Haber

In the early 20th century, German chemist Fritz Haber ((Figure)) developed a practical process for converting diatomic nitrogen, which cannot be used by plants as a nutrient, to ammonia, a form of nitrogen that is easiest for plants to absorb.

\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\)

The availability of nitrogen is a strong limiting factor to the growth of plants. Despite accounting for 78% of air, diatomic nitrogen (N2) is nutritionally unavailable due the tremendous stability of the nitrogen-nitrogen triple bond. For plants to use atmospheric nitrogen, the nitrogen must be converted to a more bioavailable form (this conversion is called nitrogen fixation).

Haber was born in Breslau, Prussia (presently Wroclaw, Poland) in December 1868. He went on to study chemistry and, while at the University of Karlsruhe, he developed what would later be known as the Haber process: the catalytic formation of ammonia from hydrogen and atmospheric nitrogen under high temperatures and pressures. For this work, Haber was awarded the 1918 Nobel Prize in Chemistry for synthesis of ammonia from its elements. The Haber process was a boon to agriculture, as it allowed the production of fertilizers to no longer be dependent on mined feed stocks such as sodium nitrate. Currently, the annual production of synthetic nitrogen fertilizers exceeds 100 million tons and synthetic fertilizer production has increased the number of humans that arable land can support from 1.9 persons per hectare in 1908 to 4.3 in 2008.

The work of Nobel Prize recipient Fritz Haber revolutionized agricultural practices in the early 20th century. His work also affected wartime strategies, adding chemical weapons to the artillery.

A photo a Fritz Haber is shown.

In addition to his work in ammonia production, Haber is also remembered by history as one of the fathers of chemical warfare. During World War I, he played a major role in the development of poisonous gases used for trench warfare. Regarding his role in these developments, Haber said, “During peace time a scientist belongs to the World, but during war time he belongs to his country.”1 Haber defended the use of gas warfare against accusations that it was inhumane, saying that death was death, by whatever means it was inflicted. He stands as an example of the ethical dilemmas that face scientists in times of war and the double-edged nature of the sword of science.

Like Haber, the products made from ammonia can be multifaceted. In addition to their value for agriculture, nitrogen compounds can also be used to achieve destructive ends. Ammonium nitrate has also been used in explosives, including improvised explosive devices. Ammonium nitrate was one of the components of the bomb used in the attack on the Alfred P. Murrah Federal Building in downtown Oklahoma City on April 19, 1995.

It has long been known that nitrogen and hydrogen react to form ammonia. However, it became possible to manufacture ammonia in useful quantities by the reaction of nitrogen and hydrogen only in the early 20th century after the factors that influence its equilibrium were understood.

To be practical, an industrial process must give a large yield of product relatively quickly. One way to increase the yield of ammonia is to increase the pressure on the system in which N2, H2, and NH3 are at equilibrium or are coming to equilibrium.

\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\)

The formation of additional amounts of ammonia reduces the total pressure exerted by the system and somewhat reduces the stress of the increased pressure.

Although increasing the pressure of a mixture of N2, H2, and NH3 will increase the yield of ammonia, at low temperatures, the rate of formation of ammonia is slow. At room temperature, for example, the reaction is so slow that if we prepared a mixture of N2 and H2, no detectable amount of ammonia would form during our lifetime. The formation of ammonia from hydrogen and nitrogen is an exothermic process:

\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}2{\text{NH}}_{3}\left(g\right)\phantom{\rule{5em}{0ex}}\text{Δ}H=-92.2\phantom{\rule{0.2em}{0ex}}\text{kJ}\)

Thus, increasing the temperature to increase the rate lowers the yield. If we lower the temperature to shift the equilibrium to favor the formation of more ammonia, equilibrium is reached more slowly because of the large decrease of reaction rate with decreasing temperature.

Part of the rate of formation lost by operating at lower temperatures can be recovered by using a catalyst. The net effect of the catalyst on the reaction is to cause equilibrium to be reached more rapidly.

In the commercial production of ammonia, conditions of about 500 °C, 150–900 atm, and the presence of a catalyst are used to give the best compromise among rate, yield, and the cost of the equipment necessary to produce and contain high-pressure gases at high temperatures ((Figure)).

Commercial production of ammonia requires heavy equipment to handle the high temperatures and pressures required. This schematic outlines the design of an ammonia plant.

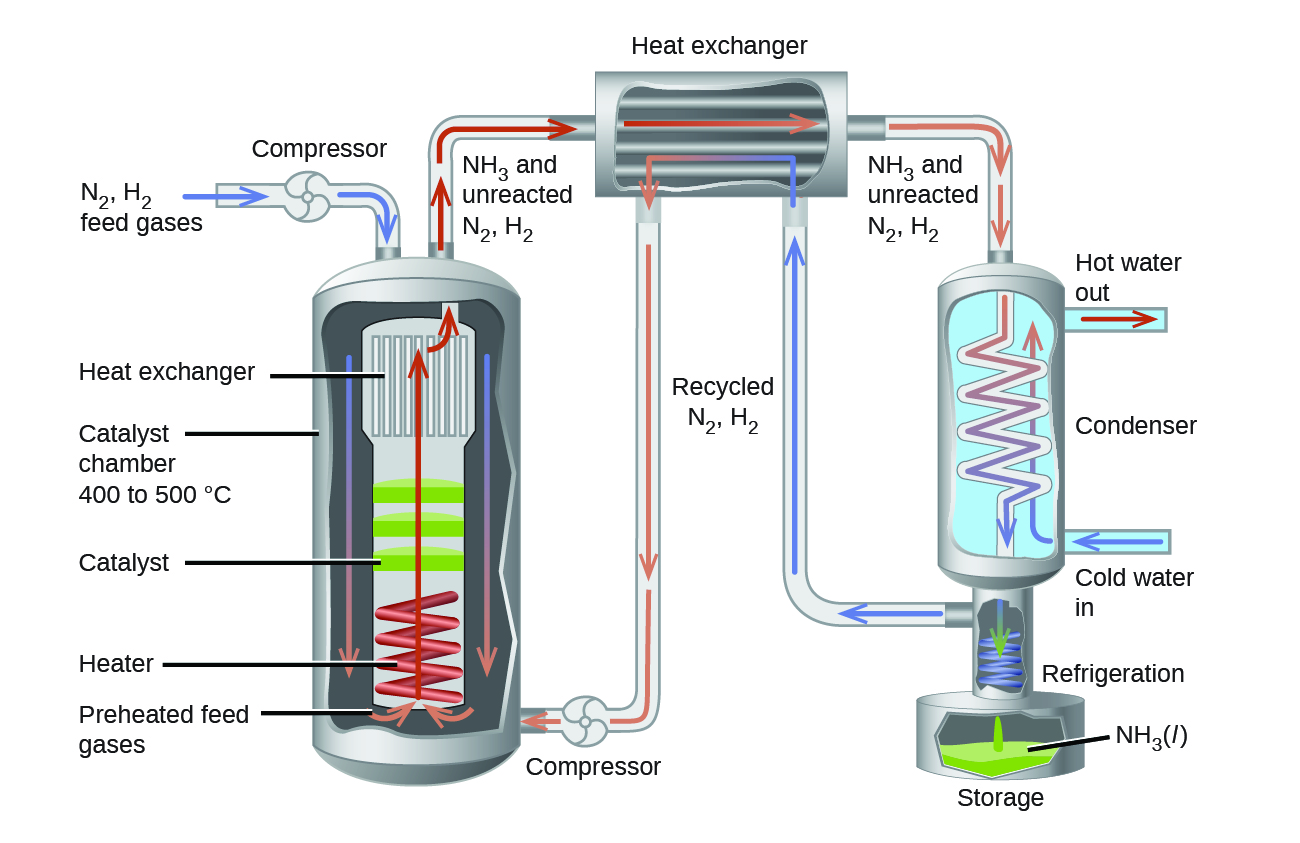
A diagram is shown that is composed of three main sections. The first section shows an intake pipe labeled with blue arrows and the terms, “N subscript 2, H subscript 2, feed gases,” and “Compressor.” This pipe leads to a large chamber with a turbine in the top section and a coil in the bottom section. From top to bottom, the sections of this chamber are labeled, “Heat exchanger,” “Catalyst chamber 400 to 500 degrees C,” “Catalyst,” “Heater,” and “Preheated feed gases.” One pipe leads from the top of this chamber with red arrows and is labeled, “N H subscript 3 and unreacted N subscript 2, H subscript 2,” while another pipe leads to the bottom of the chamber and reads, “Compressor,” and has orange arrows going through it. These two pipes are connected to a square container that is labeled, “Heat exchanger,” and has red arrows going into it from the upper pipe, orange arrows going away from it to the lower pipe and into a third system. The pipes leading into and out of the heat exchanger are labeled, “Recycled N subscript 2, H subscript 2.” The third system shows a container with an interior zig-zag-shaped pipe that sits on a base that contains a curled pipe on a storage tank. From the top of the image to the bottom are the terms, “N H subscript 3 and unreacted N subscript 2, H subscript 2,” “Condenser,” “Cold water in,” “Refrigeration,” “N H subscript 3 ( l ),” and “Storage” Blue arrows lead away from the base of this system and into the second system while other blue arrows lead into the system from the right side of the diagram and back out of the same chamber.

Among the factors affecting chemical reaction rates discussed earlier in this chapter was the presence of a catalyst, a substance that can increase the reaction rate without being consumed in the reaction. The concepts introduced in the previous section on reaction mechanisms provide the basis for understanding how catalysts are able to accomplish this very important function.

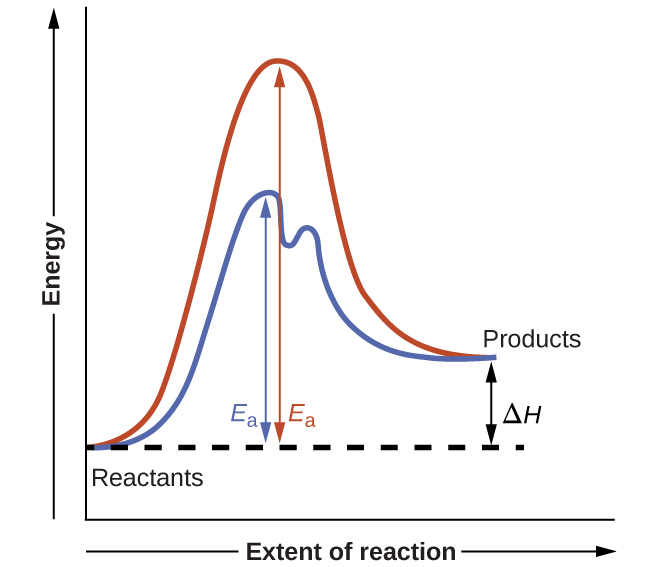
(Figure) shows reaction diagrams for a chemical process in the absence and presence of a catalyst. Inspection of the diagrams reveals several traits of these reactions. Consistent with the fact that the two diagrams represent the same overall reaction, both curves begin and end at the same energies (in this case, because products are more energetic than reactants, the reaction is endothermic). The reaction mechanisms, however, are clearly different. The uncatalyzed reaction proceeds via a one-step mechanism (one transition state observed), whereas the catalyzed reaction follows a two-step mechanism (two transition states observed) with a notably lesser activation energy. This difference illustrates the means by which a catalyst functions to accelerate reactions, namely, by providing an alternative reaction mechanism with a lower activation energy. Although the catalyzed reaction mechanism for a reaction needn’t necessarily involve a different number of steps than the uncatalyzed mechanism, it must provide a reaction path whose rate determining step is faster (lower Ea).

Reaction diagrams for an endothermic process in the absence (red curve) and presence (blue curve) of a catalyst. The catalyzed pathway involves a two-step mechanism (note the presence of two transition states) and an intermediate species (represented by the valley between the two transitions states).

A graph is shown with the label, “Extent of reaction,” appearing in a right pointing arrow below the x-axis and the label, “Energy,” in an upward pointing arrow just left of the y-axis. Approximately one-fifth of the way up the y-axis, a very short, somewhat flattened portion of both a red and a blue curve are shown. This region is labeled “Reactants.” A red concave down curve extends upward to reach a maximum near the height of the y-axis. From the peak, the curve continues downward to a second horizontally flattened region at a height of about one-third the height of the y-axis. This flattened region is labeled, “Products.” A second curve is drawn in blue with the same flattened regions at the start and end of the curve. The height of this curve is about two-thirds the height of the first curve and just right of its maximum, the curve dips low, then rises back and continues a downward trend at a lower height, but similar to that of the red curve. A horizontal dashed straight line extends from the point where both curves start in the “Reactants” region. A double sided arrow extends from the “Products” region at the end of both curves to this horizontal dashed line. This is labeled “capital delta H.” A double sided arrow extends from the dashed horizontal line to the peak of the red concave down curve. This arrow is labeled “E subscript a.” Another double sided arrow extends from the dashed horizontal line to the peak of the blue curve. This arrow is labeled “E subscript a.”

Reaction Diagrams for Catalyzed Reactions The two reaction diagrams here represent the same reaction: one without a catalyst and one with a catalyst. Estimate the activation energy for each process, and identify which one involves a catalyst.

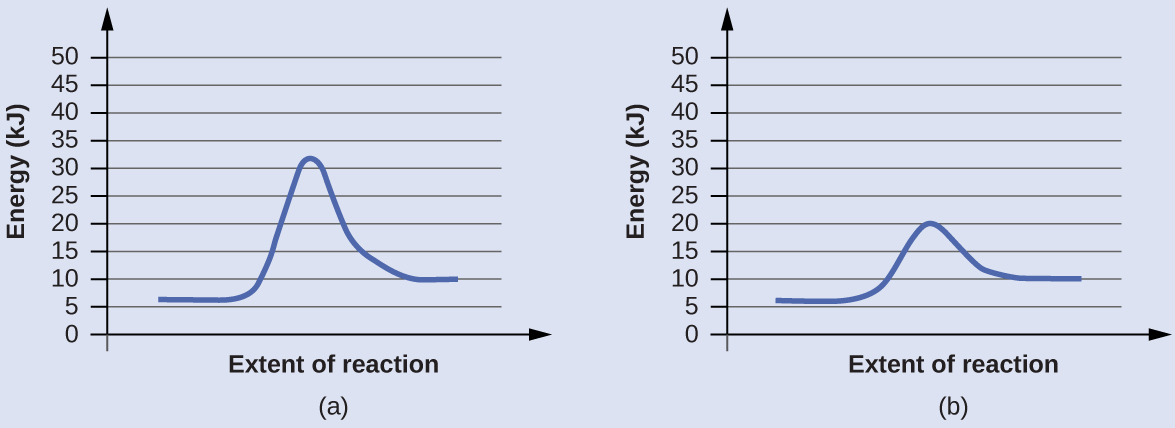
In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeled, “Energy ( k J ).” The y-axes are marked off from 0 to 50 in intervals of five. In a, a blue curve is shown. It begins with a horizontal segment at about 6. The curve then rises sharply near the middle to reach a maximum of about 32 and similarly falls to another horizontal segment at about 10. In b, the curve begins and ends similarly, but the maximum reached near the center of the graph is only 20.

Solution Activation energies are calculated by subtracting the reactant energy from the transition state energy.

\(\text{diagram (a):}\phantom{\rule{0.2em}{0ex}}{E}_{\text{a}}=32\phantom{\rule{0.2em}{0ex}}\text{kJ}-6\phantom{\rule{0.2em}{0ex}}\text{kJ}=26\phantom{\rule{0.2em}{0ex}}\text{kJ}\)
\(\text{diagram (b):}\phantom{\rule{0.2em}{0ex}}{E}_{\text{a}}=20\phantom{\rule{0.2em}{0ex}}\text{kJ}-6\phantom{\rule{0.2em}{0ex}}\text{kJ}=14\phantom{\rule{0.2em}{0ex}}\text{kJ}\)

The catalyzed reaction is the one with lesser activation energy, in this case represented by diagram (b).

Check Your Learning Reaction diagrams for a chemical process with and without a catalyst are shown below. Both reactions involve a two-step mechanism with a rate-determining first step. Compute activation energies for the first step of each mechanism, and identify which corresponds to the catalyzed reaction. How do the second steps of these two mechanisms compare?

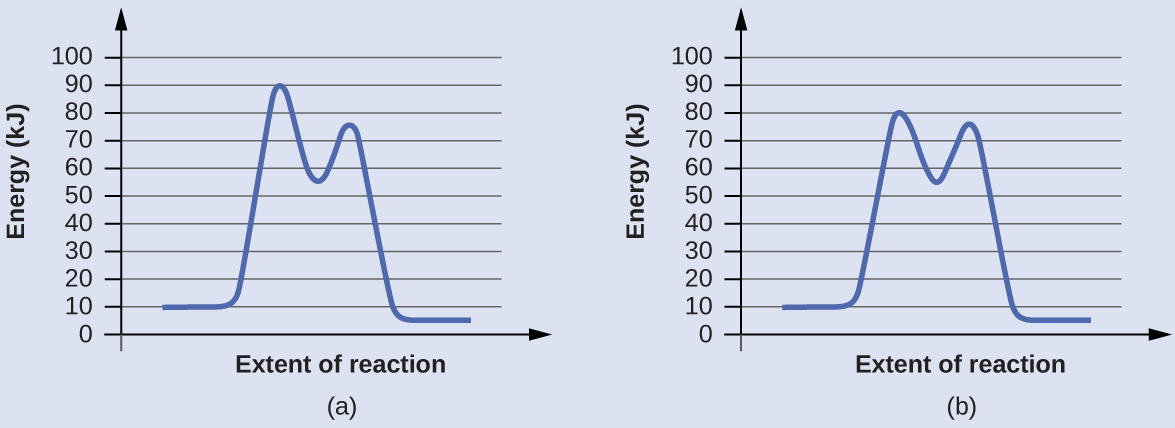
In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeledc “Energy (k J).” The y-axes are marked off from 0 to 100 at intervals of 10. In a, a blue curve is shown. It begins with a horizontal segment at about 10. The curve then rises sharply near the middle to reach a maximum of about 91, then sharply falls to about 52, again rises sharply to about 73 and falls to another horizontal segment at about 5. In b, the curve begins and ends similarly, but the first peak reaches about 81, drops to about 55, then rises to about 77 before falling to the horizontal region at about 5.

Answer:

For the first step, Ea = 80 kJ for (a) and 70 kJ for (b), so diagram (b) depicts the catalyzed reaction. Activation energies for the second steps of both mechanisms are the same, 20 kJ.

Homogeneous Catalysts

A homogeneous catalyst is present in the same phase as the reactants. It interacts with a reactant to form an intermediate substance, which then decomposes or reacts with another reactant in one or more steps to regenerate the original catalyst and form product.

As an important illustration of homogeneous catalysis, consider the earth’s ozone layer. Ozone in the upper atmosphere, which protects the earth from ultraviolet radiation, is formed when oxygen molecules absorb ultraviolet light and undergo the reaction:

\(3{\text{O}}_{2}\left(g\right)\stackrel{\phantom{\rule{0.7em}{0ex}}hv\phantom{\rule{0.7em}{0ex}}}{\to }2{\text{O}}_{3}\left(g\right)\)

Ozone is a relatively unstable molecule that decomposes to yield diatomic oxygen by the reverse of this equation. This decomposition reaction is consistent with the following two-step mechanism:

\(\begin{array}{}\\ {\text{O}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{O}}_{2}+\text{O}\\ \text{O}+{\text{O}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}2{\text{O}}_{2}\end{array}\)

A number of substances can catalyze the decomposition of ozone. For example, the nitric oxide -catalyzed decomposition of ozone is believed to occur via the following three-step mechanism:

\(\begin{array}{}\\ \text{NO(}g\right)+{\text{O}}_{\text{3}}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NO}}_{\text{2}}\left(g\right)+{\text{O}}_{\text{2}}\left(g\right)\\ {\text{O}}_{3}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{O}}_{2}\left(g\right)+\text{O}\left(g\right)\\ {\text{NO}}_{2}\left(g\right)+\text{O}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{NO}\left(g\right)+{\text{O}}_{2}\left(g\right)\end{array}\)

As required, the overall reaction is the same for both the two-step uncatalyzed mechanism and the three-step NO-catalyzed mechanism:

\(2{\text{O}}_{3}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}3{\text{O}}_{2}\left(g\right)\)

Notice that NO is a reactant in the first step of the mechanism and a product in the last step. This is another characteristic trait of a catalyst: Though it participates in the chemical reaction, it is not consumed by the reaction.

Mario J. Molina

The 1995 Nobel Prize in Chemistry was shared by Paul J. Crutzen, Mario J. Molina ((Figure)), and F. Sherwood Rowland “for their work in atmospheric chemistry, particularly concerning the formation and decomposition of ozone.”2 Molina, a Mexican citizen, carried out the majority of his work at the Massachusetts Institute of Technology (MIT).

(a) Mexican chemist Mario Molina (1943 –) shared the Nobel Prize in Chemistry in 1995 for his research on (b) the Antarctic ozone hole. (credit a: courtesy of Mario Molina; credit b: modification of work by NASA)

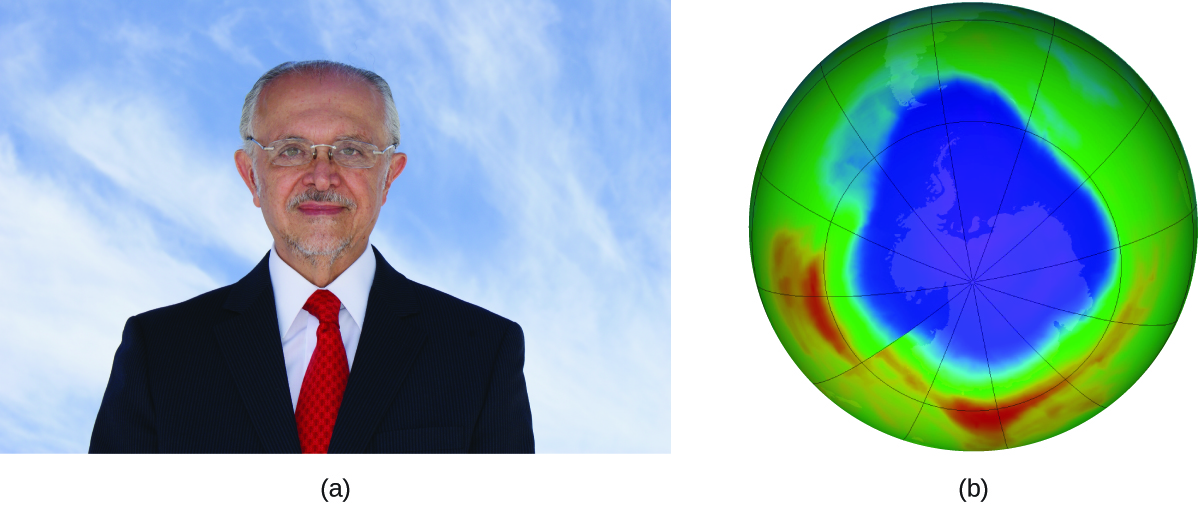
A photograph is shown of Mario Molina. To the right of the photo, an image of Earth’s southern hemisphere is shown with a central circular region in purple with a radius of about half that of the entire hemisphere. Just outside this region is a narrow royal blue band, followed by an outer thin turquoise blue band. The majority of the outermost region is green. Two small bands of yellow are present in the lower regions of the image.

In 1974, Molina and Rowland published a paper in the journal Nature detailing the threat of chlorofluorocarbon gases to the stability of the ozone layer in earth’s upper atmosphere. The ozone layer protects earth from solar radiation by absorbing ultraviolet light. As chemical reactions deplete the amount of ozone in the upper atmosphere, a measurable “hole” forms above Antarctica, and an increase in the amount of solar ultraviolet radiation— strongly linked to the prevalence of skin cancers—reaches earth’s surface. The work of Molina and Rowland was instrumental in the adoption of the Montreal Protocol, an international treaty signed in 1987 that successfully began phasing out production of chemicals linked to ozone destruction.

Molina and Rowland demonstrated that chlorine atoms from human-made chemicals can catalyze ozone destruction in a process similar to that by which NO accelerates the depletion of ozone. Chlorine atoms are generated when chlorocarbons or chlorofluorocarbons—once widely used as refrigerants and propellants—are photochemically decomposed by ultraviolet light or react with hydroxyl radicals. A sample mechanism is shown here using methyl chloride:

\({\text{CH}}_{3}\text{Cl}+\text{OH}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{Cl}+\text{other products}\)

Chlorine radicals break down ozone and are regenerated by the following catalytic cycle:

\(\begin{array}{}\\ \text{Cl}+{\text{O}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{ClO}+{\text{O}}_{2}\\ \text{ClO}+\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{Cl}+{\text{O}}_{2}\\ \text{overall Reaction:}\phantom{\rule{0.2em}{0ex}}{\text{O}}_{3}+\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}2{\text{O}}_{2}\end{array}\)

A single monatomic chlorine can break down thousands of ozone molecules. Luckily, the majority of atmospheric chlorine exists as the catalytically inactive forms Cl2 and ClONO2.

Since receiving his portion of the Nobel Prize, Molina has continued his work in atmospheric chemistry at MIT.

Glucose-6-Phosphate Dehydrogenase Deficiency

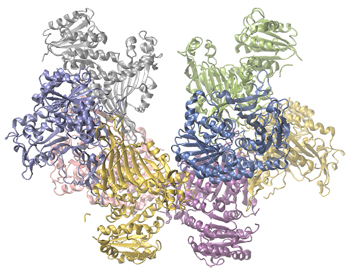
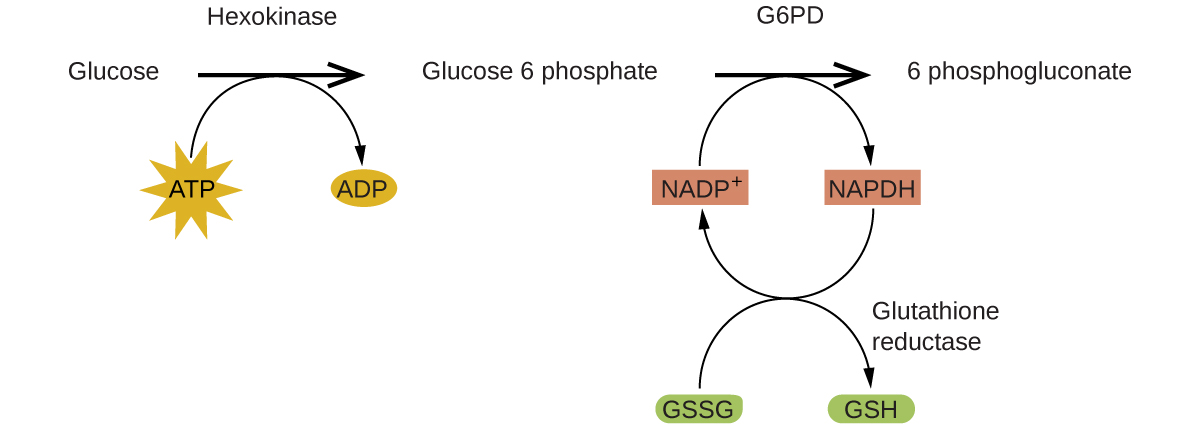
Enzymes in the human body act as catalysts for important chemical reactions in cellular metabolism. As such, a deficiency of a particular enzyme can translate to a life-threatening disease. G6PD (glucose-6-phosphate dehydrogenase) deficiency, a genetic condition that results in a shortage of the enzyme glucose-6-phosphate dehydrogenase, is the most common enzyme deficiency in humans. This enzyme, shown in (Figure), is the rate-limiting enzyme for the metabolic pathway that supplies NADPH to cells ((Figure)).

Glucose-6-phosphate dehydrogenase is a rate-limiting enzyme for the metabolic pathway that supplies NADPH to cells.

A colorful model of the Glucose-6-phosphate dehydrogenase structure is shown. The molecule has two distinct lobes which are filled with spiraled ribbon-like regions of yellow, lavender, blue, silver, green, and pink.

A disruption in this pathway can lead to reduced glutathione in red blood cells; once all glutathione is consumed, enzymes and other proteins such as hemoglobin are susceptible to damage. For example, hemoglobin can be metabolized to bilirubin, which leads to jaundice, a condition that can become severe. People who suffer from G6PD deficiency must avoid certain foods and medicines containing chemicals that can trigger damage their glutathione-deficient red blood cells.

In the mechanism for the pentose phosphate pathway, G6PD catalyzes the reaction that regulates NADPH, a co-enzyme that regulates glutathione, an antioxidant that protects red blood cells and other cells from oxidative damage.

A reaction mechanism is diagrammed in this figure. At the left, the name Glucose is followed by a horizontal, right pointing arrow, labeled, “Hexokinase.” Below this arrow and to the left is a yellow star shape labeled, “A T P.” A curved arrow extends from this shape to the right pointing arrow, and down to the right to a small brown oval labeled, “A D P.” To the right of the horizontal arrow is the name Glucose 6 phosphate, which is followed by another horizontal, right pointing arrow which is labeled, “G 6 P D.” A small orange rectangle below and left of this arrow is labeled “N A D P superscript plus.” A curved arrow extends from this shape to the right pointing arrow, and down to the right to a small salmon-colored rectangle labeled “N A P D H.” A curved arrow extends from this shape below and to the left, back to the orange rectangle labeled, “N A D P superscript plus.” Another curved arrow extends from a green oval labeled “G S S G” below the orange rectangle, up to the arrow curving back to the orange rectangle. This last curved arrow continues on to the lower right to a second green oval labeled, “G S H.” The end of this curved arrow is labeled, “Glutathione reductase.” To the right of the rightmost horizontal arrow appears the name 6 phosphogluconate.

Heterogeneous Catalysts

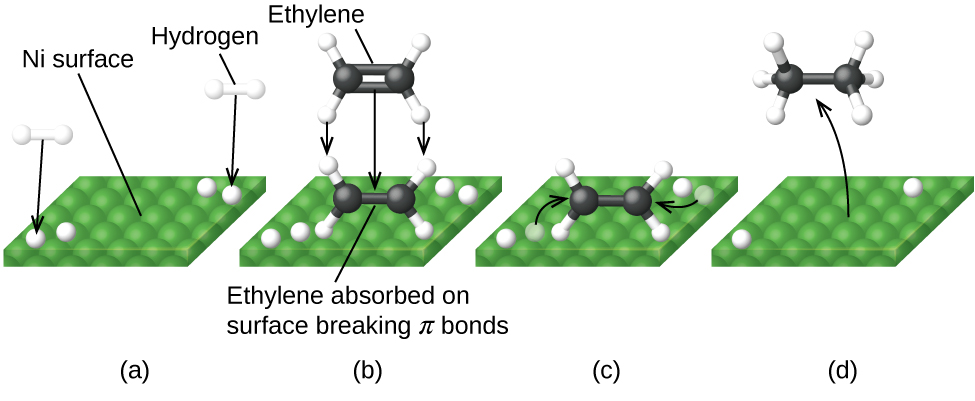
A heterogeneous catalyst is a catalyst that is present in a different phase (usually a solid) than the reactants. Such catalysts generally function by furnishing an active surface upon which a reaction can occur. Gas and liquid phase reactions catalyzed by heterogeneous catalysts occur on the surface of the catalyst rather than within the gas or liquid phase.

Heterogeneous catalysis typically involves the following processes:

  1. Adsorption of the reactant(s) onto the surface of the catalyst
  2. Activation of the adsorbed reactant(s)
  3. Reaction of the adsorbed reactant(s)
  4. Desorption of product(s) from the surface of the catalyst

(Figure) illustrates the steps of a mechanism for the reaction of compounds containing a carbon–carbon double bond with hydrogen on a nickel catalyst. Nickel is the catalyst used in the hydrogenation of polyunsaturated fats and oils (which contain several carbon–carbon double bonds) to produce saturated fats and oils (which contain only carbon–carbon single bonds).

Mechanism for the Ni-catalyzed reaction \({\text{C}}_{2}{\text{H}}_{4}+{\text{H}}_{2}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{C}}_{2}{\text{H}}_{6}.\) (a) Hydrogen is adsorbed on the surface, breaking the H–H bonds and forming Ni–H bonds. (b) Ethylene is adsorbed on the surface, breaking the C-C π-bond and forming Ni–C bonds. (c) Atoms diffuse across the surface and form new C–H bonds when they collide. (d) C2H6 molecules desorb from the Ni surface.

In this figure, four diagrams labeled a through d are shown. In each, a green square surface is shown in perspective to provide a three-dimensional appearance. In a, the label “N i surface” is placed above with a line segment extending to the green square. At the lower left and upper right, pairs of white spheres bonded tougher together appear as well as white spheres on the green surface. Black arrows are drawn from each of the white spheres above the surface to the white sphere on the green surface. In b, the white spheres are still present on the green surface. Near the center of this surface is a molecule with two central black spheres with a double bond indicated by two horizontal black rods between them. Above and below to the left and right, a total of four white spheres are connected to the black spheres with white rods. A line segment extends from this structure to the label, “Ethylene absorbed on surface breaking pi bonds.” Just above this is a nearly identical structure greyed out with three downward pointing arrows to the black and white structure to indicate downward motion. The label “Ethylene” at the top of the diagram is connected to the greyed out structure with a line segment. In c, the diagram is very similar to b except that the greyed out structure and labels are gone and one of the white spheres near the black and white structure in each pair on the green surface is greyed out. Arrows point from the greyed out white spheres to the double bond between the two black spheres. In d, only a single white sphere remains from each pair in the green surface. A curved arrow points from the middle of the green surface to a model above with two central black spheres with a single black rod indicating a single bond between them. Each of the black rods has three small white spheres bonded as indicated by white rods between the black spheres and the small white spheres. The four bonds around each black sphere are evenly distributed about the black spheres.

Many important chemical products are prepared via industrial processes that use heterogeneous catalysts, including ammonia, nitric acid, sulfuric acid, and methanol. Heterogeneous catalysts are also used in the catalytic converters found on most gasoline-powered automobiles ((Figure)).

Automobile Catalytic Converters

Scientists developed catalytic converters to reduce the amount of toxic emissions produced by burning gasoline in internal combustion engines. By utilizing a carefully selected blend of catalytically active metals, it is possible to effect complete combustion of all carbon-containing compounds to carbon dioxide while also reducing the output of nitrogen oxides. This is particularly impressive when we consider that one step involves adding more oxygen to the molecule and the other involves removing the oxygen ((Figure)).

A catalytic converter allows for the combustion of all carbon-containing compounds to carbon dioxide, while at the same time reducing the output of nitrogen oxide and other pollutants in emissions from gasoline-burning engines.

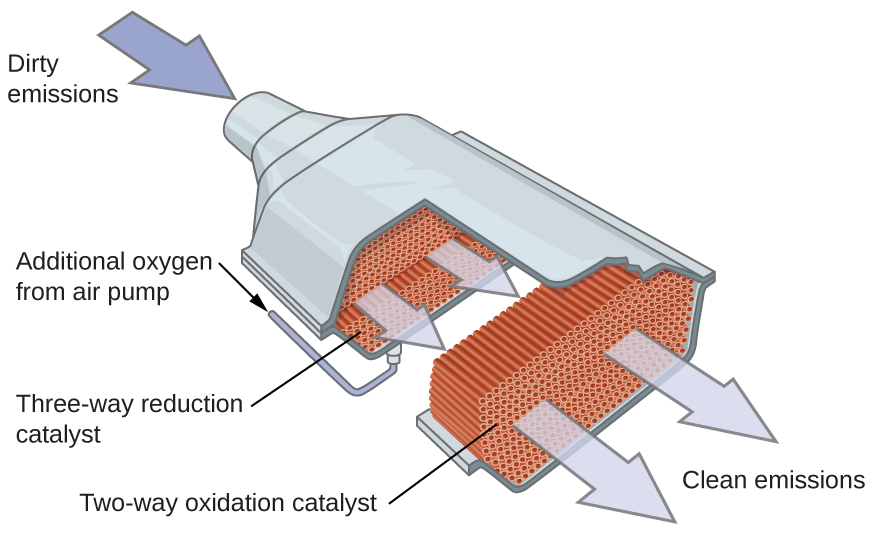
An image is shown of a catalytic converter. At the upper left, a blue arrow pointing into a pipe that enters a larger, widened chamber is labeled, “Dirty emissions.” A small black arrow that points to the lower right is positioned along the upper left side of the widened region. This arrow is labeled, “Additional oxygen from air pump.” The image shows the converter with the upper surface removed, exposing a red-brown interior. The portion of the converter closest to the dirty emissions inlet shows small, round components in an interior layer. This layer is labeled “Three-way reduction catalyst.” The middle region shows closely packed small brown rods that are aligned parallel to the dirty emissions inlet pipe. The final quarter of the interior of the catalytic converter again shows a layer of closely packed small red brown circles. Two large light grey arrows extend from this layer to the open region at the lower right of the image to the label “Clean emissions.”

Most modern, three-way catalytic converters possess a surface impregnated with a platinum-rhodium catalyst, which catalyzes the conversion of nitric oxide into dinitrogen and oxygen as well as the conversion of carbon monoxide and hydrocarbons such as octane into carbon dioxide and water vapor:

\(\begin{array}{l}2{\text{NO}}_{\text{2}}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{N}}_{\text{2}}\left(g\right)+2{\text{O}}_{\text{2}}\left(g\right)\\ 2\text{CO(}g\right)+{\text{O}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}2{\text{CO}}_{\text{2}}\left(g\right)\\ 2{\text{C}}_{8}{\text{H}}_{18}\left(g\right)+25{\text{O}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}16{\text{CO}}_{2}\left(g\right)+18{\text{H}}_{2}\text{O}\left(g\right)\end{array}\)

In order to be as efficient as possible, most catalytic converters are preheated by an electric heater. This ensures that the metals in the catalyst are fully active even before the automobile exhaust is hot enough to maintain appropriate reaction temperatures.

Enzyme Structure and Function

The study of enzymes is an important interconnection between biology and chemistry. Enzymes are usually proteins (polypeptides) that help to control the rate of chemical reactions between biologically important compounds, particularly those that are involved in cellular metabolism. Different classes of enzymes perform a variety of functions, as shown in (Figure).

Classes of Enzymes and Their Functions
Class Function
oxidoreductases redox reactions
transferases transfer of functional groups
hydrolases hydrolysis reactions
lyases group elimination to form double bonds
isomerases isomerization
ligases bond formation with ATP hydrolysis

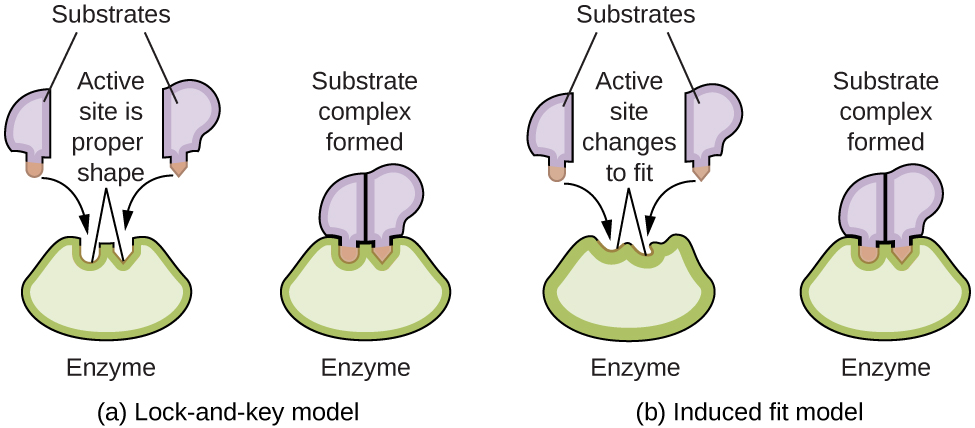
Enzyme molecules possess an active site, a part of the molecule with a shape that allows it to bond to a specific substrate (a reactant molecule), forming an enzyme-substrate complex as a reaction intermediate. There are two models that attempt to explain how this active site works. The most simplistic model is referred to as the lock-and-key hypothesis, which suggests that the molecular shapes of the active site and substrate are complementary, fitting together like a key in a lock. The induced fit hypothesis, on the other hand, suggests that the enzyme molecule is flexible and changes shape to accommodate a bond with the substrate. This is not to suggest that an enzyme’s active site is completely malleable, however. Both the lock-and-key model and the induced fit model account for the fact that enzymes can only bind with specific substrates, since in general a particular enzyme only catalyzes a particular reaction ((Figure)).

(a) According to the lock-and-key model, the shape of an enzyme’s active site is a perfect fit for the substrate. (b) According to the induced fit model, the active site is somewhat flexible, and can change shape in order to bond with the substrate.

A diagram is shown of two possible interactions of an enzyme and a substrate. In a, which is labeled “Lock-and-key,” two diagrams are shown. The first shows a green wedge-like shape with two small depressions in the upper surface of similar size, but the depression on the left has a curved shape, and the depression on the right has a pointed shape. This green shape is labeled “Enzyme.” Just above this shape are two smaller, irregular, lavender shapes each with a projection from its lower surface. The lavender shape on the left has a curved projection which matches the shape of the depression on the left in the green shape below. This projection is shaded orange and has a curved arrow extending from in to the matching depression in the green shape below. Similarly, the lavender shape on the right has a projection with a pointed tip which matches the shape of the depression on the right in the green shape below. This projection is shaded orange and has a curved arrow extending from in to the matching depression in the green shape below. Two line segments extend from the depressions in the green shape to form an inverted V shape above the depressions. Above this and between the lavender shapes is the label, “Active site is proper shape.” The label “Substrates” is at the very top of the diagram with line segments extending to the two lavender shapes. To the right of this diagram is a second diagram showing the lavender shapes positioned next to each other, fit snugly into the depressions in the green shape, which is labeled “Enzyme.” Above this diagram is the label, “Substrate complex formed.” In b, which is labeled “Induced fit,” two diagrams are shown. The first shows a green wedge-like shape with two small depressions in the upper surface of similar size, but irregular shape. This green shape is labeled “Enzyme.” Just above this shape are two smaller irregular lavender shapes each with a projection from its lower surface. The lavender shape on the left has a curved projection. This projection is shaded orange and has a curved arrow extending from it to the irregular depression just below it in the green shape below. Similarly, the lavender shape on the right has a projection with a pointed tip. This projection is shaded orange and has a curved arrow extending from it to the irregular depression just below it in the green shape below. Two line segments extend from the depressions in the green shape to form an inverted V shape above the depressions. Above this and between the lavender shapes is the label, “Active site changes to fit.” The label, “Substrates” is at the very top of the diagram with line segments extending to the two lavender shapes. To the right of this diagram is a second diagram showing the purple shapes positioned next to each other, fit snugly into the depressions in the green shape, which is labeled “Enzyme.” Above this diagram is the label “Substrate complex formed.” The projections from the lavender shapes match the depression shapes in the green shape, resulting in a proper fit.

The connection between the rate of a reaction and its equilibrium constant is one we can easily determine with just a bit of algebraic substitution. For a reaction where substance A forms B (and the reverse)

\(A⇌B\)

The rate of the forward reaction is

\(\text{Rate}\left(f\right)=k\left(f\right)\left[A\right]\)

And the rate of the reverse reaction is

\(\text{Rate}\left(r\right)=k\left(r\right)\left[B\right]\)

Once equilibrium is established, the rates of the forward and reverse reactions are equal:

\(\text{Rate}\left(f\right)=\text{Rate}\left(r\right)=k\left(f\right)\left[A\right]=k\left(r\right)\left[B\right]\)

Rearranging a bit, we get

\({\text{Rate}}_{f}={\text{Rate}}_{r}\phantom{\rule{0.2em}{0ex}}\text{so}\phantom{\rule{0.2em}{0ex}}k\left(f\right)\left[A\right]=k\left(r\right)\left[B\right]\)

Also recall that the equilibrium constant is simply the ratio of product to reactant concentration at equilibrium:

\(\frac{k\left(f\right)}{k\left(r\right)}=\frac{\left[B\right]}{\left[A\right]}\)
\(K=\frac{\left[B\right]}{\left[A\right]}\)

So the equilibrium constant turns out to be the ratio of the forward to the reverse rate constants. This relationship also helps cement our understanding of the nature of a catalyst. That is, a catalyst does not change the fundamental equilibrium (or the underlying thermodynamics) of a reaction. Rather, what it does is alter the rate constant for the reaction – that is, both rate constants, forward and reverse, equally. In doing so, catalysts usually speed up the rate at which reactions attain equilibrium (though they can be used to slow down the rate of reaction as well!).

Key Concepts and Summary

Catalysts affect the rate of a chemical reaction by altering its mechanism to provide a lower activation energy, but they do not affect equilibrium. Catalysts can be homogenous (in the same phase as the reactants) or heterogeneous (a different phase than the reactants).

Chemistry End of Chapter Exercises

Account for the increase in reaction rate brought about by a catalyst.

The general mode of action for a catalyst is to provide a mechanism by which the reactants can unite more readily by taking a path with a lower reaction energy. The rates of both the forward and the reverse reactions are increased, leading to a faster achievement of equilibrium.

Compare the functions of homogeneous and heterogeneous catalysts.

Consider this scenario and answer the following questions: Chlorine atoms resulting from decomposition of chlorofluoromethanes, such as CCl2F2, catalyze the decomposition of ozone in the atmosphere. One simplified mechanism for the decomposition is:
 \(\begin{array}{}\\ \\ {\text{O}}_{3}\stackrel{\phantom{\rule{0.2em}{0ex}}\text{sunlight}\phantom{\rule{0.2em}{0ex}}}{\to }{\text{O}}_{2}+\text{O}\\ {\text{O}}_{3}+\text{Cl}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{O}}_{2}+\text{ClO}\\ \text{ClO}+\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{Cl}+{\text{O}}_{2}\end{array}\)

(a) Explain why chlorine atoms are catalysts in the gas-phase transformation:
 \(2{\text{O}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}3{\text{O}}_{2}\)

(b) Nitric oxide is also involved in the decomposition of ozone by the mechanism:
 \(\begin{array}{}\\ {\text{O}}_{3}\stackrel{\phantom{\rule{0.2em}{0ex}}\text{sunlight}\phantom{\rule{0.2em}{0ex}}}{\to }{\text{O}}_{2}+\text{O}\\ {\text{O}}_{3}+\text{NO}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{NO}}_{2}+{\text{O}}_{2}\\ {\text{NO}}_{2}+\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{NO}+{\text{O}}_{2}\end{array}\)

Is NO a catalyst for the decomposition? Explain your answer.

(a) Chlorine atoms are a catalyst because they react in the second step but are regenerated in the third step. Thus, they are not used up, which is a characteristic of catalysts. (b) NO is a catalyst for the same reason as in part (a).

Water gas is a 1:1 mixture of carbon monoxide and hydrogen gas and is called water gas because it is formed from steam and hot carbon in the following reaction: \({\text{H}}_{2}\text{O}\left(g\right)+\text{C}\left(s\right)⇌{\text{H}}_{2}\left(g\right)+\text{CO}\left(g\right).\) Methanol, a liquid fuel that could possibly replace gasoline, can be prepared from water gas and hydrogen at high temperature and pressure in the presence of a suitable catalyst. What will happen to the concentrations of H2, CO, and CH3OH at equilibrium if more catalyst is added?

no changes.

Nitrogen and oxygen react at high temperatures. What will happen to the concentrations of N2, O2, and NO at equilibrium if a catalyst is added?

For each of the following pairs of reaction diagrams, identify which of the pair is catalyzed:

(a)

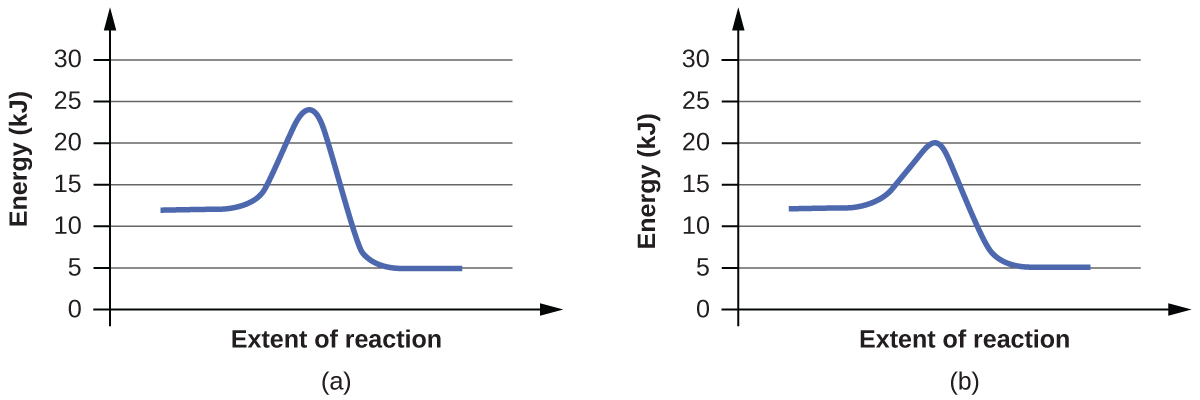
In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeled, “Energy (k J).” The y-axis of the first graph is marked off from 0 to 30 in intervals of 5. The y-axis of the second graph is marked off from 0 to 25 by intervals of 5. In a, a blue curve is shown. It begins with a horizontal region at about 12. The curve then rises sharply near the middle to reach a maximum of about 24 and similarly falls to another horizontal segment at 5. In b, the curve begins and ends similarly, but the maximum reached near the center of the graph is only 20.

(b)

In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeled, “Energy.” The y-axes are marked off from 0 to 50 in intervals of 5. In a, a blue curve is shown. It begins with a horizontal region at about 2. The curve then rises sharply near the middle to reach a maximum of about 43 and similarly falls to another horizontal segment at 15. In b, the curve begins and ends similarly, but the maximum reached near the center of the graph is only about 32.

For each of the following pairs of reaction diagrams, identify which of the pairs is catalyzed:

(a)

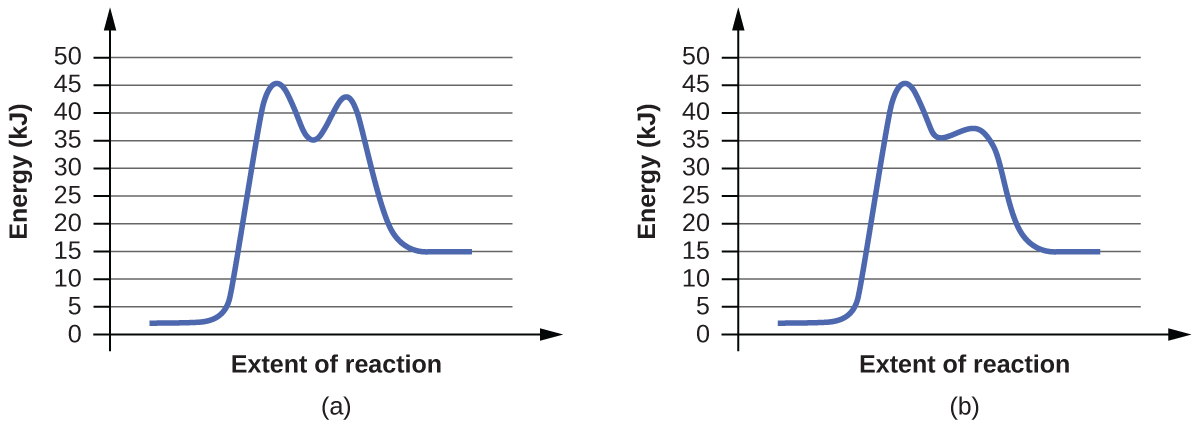
In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction” and the y-axes are labeled, “Energy (k J).” The y-axes are marked off from 0 to 50 at intervals of 5. In a, a blue curve is shown. It begins with a horizontal segment at about 2J. The curve then rises sharply near the middle to reach a maximum of about 46, then sharply falls to about 35, again rises to about 38 and falls to another horizontal segment at about 15. In b, the curve begins and ends similarly, but the first peak reaches about 46, drops to about 35, then rises to about 43 before falling to the horizontal region at about 15.

(b)

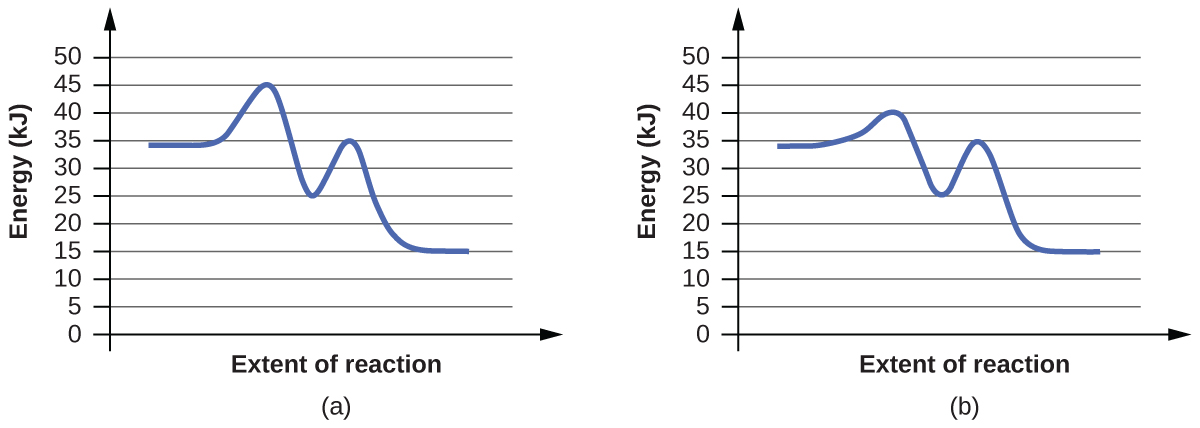
In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeled, “Energy (k J).” The y-axes are marked off from 0 to 50 at intervals of 5. In a, a blue curve is shown. It begins with a horizontal segment at about 34. The curve then rises sharply near the middle to reach a maximum of about 45, then sharply falls to about 25, again rises sharply to about 35 and falls to another horizontal segment at about 15. In b, the curve begins and ends similarly, but the first peak reaches about 40, drops to 25, then rises to 35 before falling to the horizontal region at about 15.

The lowering of the transition state energy indicates the effect of a catalyst. (a) B; (b) B

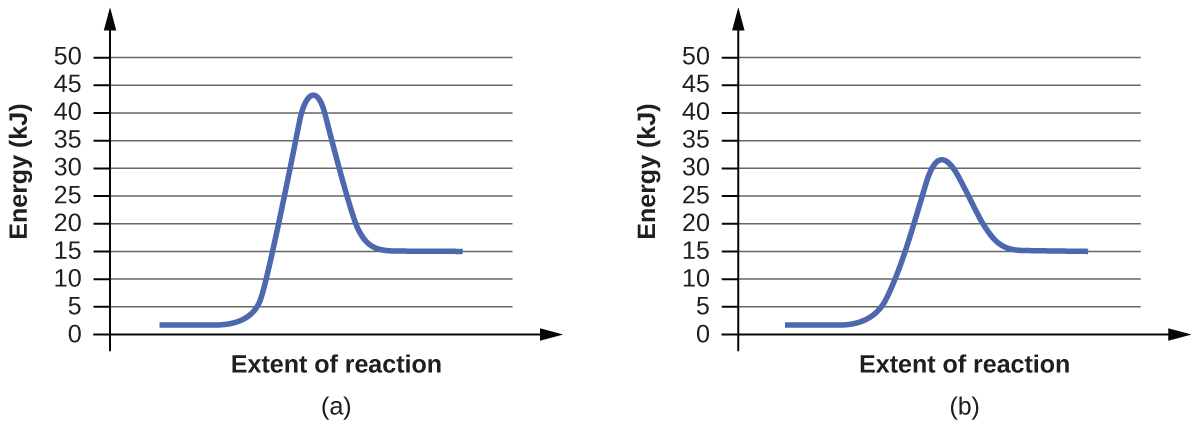
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:

(a)

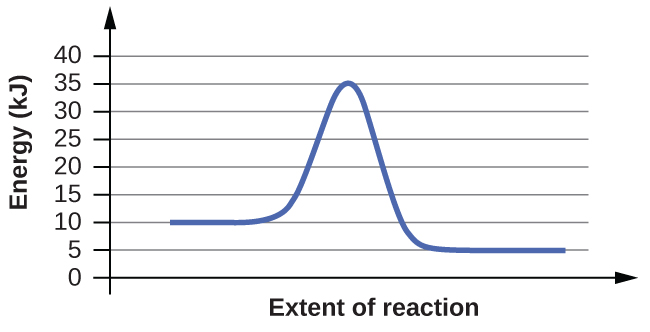
This figure shows a graph. The x-axis is labeled, “Extent of reaction,” and the y-axis is labeled, “Energy (k J).” The y-axis is marked off from 0 to 40 at intervals of 5. A blue curve is shown. It begins with a horizontal region at 10. The curve then rises sharply near the middle to reach a maximum of 35 and similarly falls to another horizontal segment at 5.

(b)

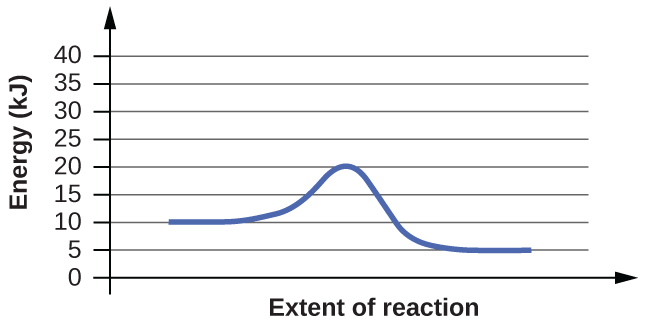
This figure shows a graph. The x-axis is labeled, “Extent of reaction,” and the y-axis is labeled, “Energy (k J).” The y-axis is marked off from 0 to 40 at intervals of 5. A blue curve is shown. It begins with a horizontal region at 10. The curve then rises sharply near the middle to reach a maximum of 20 and similarly falls to another horizontal segment at 5.

For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:

(a)

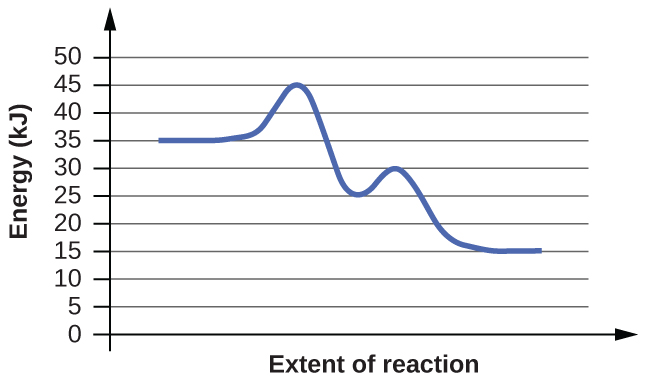
In this figure, a graph is shown. The x-axis is labeled, “Extent of reaction,” and the y-axis is labeled, “Energy (k J).” A blue curve is shown. It begins with a horizontal segment at about 35. The curve then rises sharply near the middle to reach a maximum of about 45, then sharply falls to about 24, again rises to about 30 and falls to another horizontal segment at about 15.

(b)

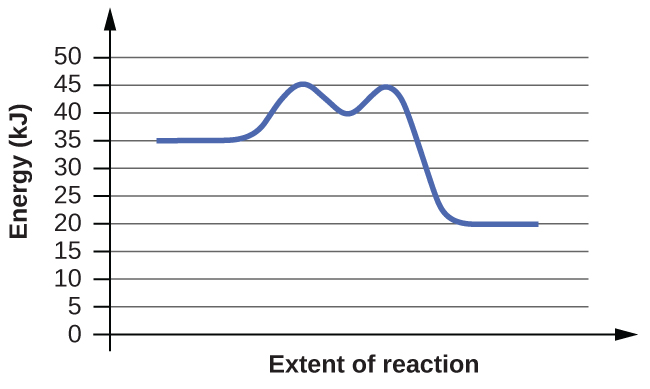
In this figure, a graph is shown. The x-axis is labeled, “Extent of reaction,” and the y-axis is labeled, “Energy (k J).” A blue curve is shown. It begins with a horizontal segment at about 35. The curve then rises sharply near the middle to reach a maximum of about 45, then sharply falls to about 40, again rises to about 45 and falls to another horizontal segment at about 20.

The energy needed to go from the initial state to the transition state is (a) 10 kJ; (b) 10 kJ

Assuming the diagrams in (Figure) represent different mechanisms for the same reaction, which of the reactions has the faster rate?

Consider the similarities and differences in the two reaction diagrams shown in (Figure). Do these diagrams represent two different overall reactions, or do they represent the same overall reaction taking place by two different mechanisms? Explain your answer.

Both diagrams describe two-step, exothermic reactions, but with different changes in enthalpy, suggesting the diagrams depict two different overall reactions.

Footnotes

  • 1Herrlich, P. “The Responsibility of the Scientist: What Can History Teach Us About How Scientists Should Handle Research That Has the Potential to Create Harm?” EMBO Reports 14 (2013): 759–764.
  • 2“The Nobel Prize in Chemistry 1995,” Nobel Prize.org, accessed February 18, 2015, http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1995/.

Glossary

heterogeneous catalyst
catalyst present in a different phase from the reactants, furnishing a surface at which a reaction can occur
homogeneous catalyst
catalyst present in the same phase as the reactants

License

Icon for the Creative Commons Attribution 4.0 International License

Atoms First / OpenStax Copyright © 2018 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book