13 Chemical Formulas

[latexpage]

Learning Objectives

By the end of this section, you will be able to:

  • Symbolize the composition of molecules using molecular formulas and empirical formulas
  • Represent the bonding arrangement of atoms within molecules using structural formulas
  • Define the amount unit mole and the related quantity Avogadro’s number
  • Explain the relation between mass, moles, and numbers of atoms or molecules and perform calculations deriving these quantities from one another

Molecular and Empirical Formulas

A molecular formula is a representation of a molecule that uses chemical symbols to indicate the types of atoms followed by subscripts to show the number of atoms of each type in the molecule. (A subscript is used only when more than one atom of a given type is present.) Molecular formulas are also used as abbreviations for the names of compounds.

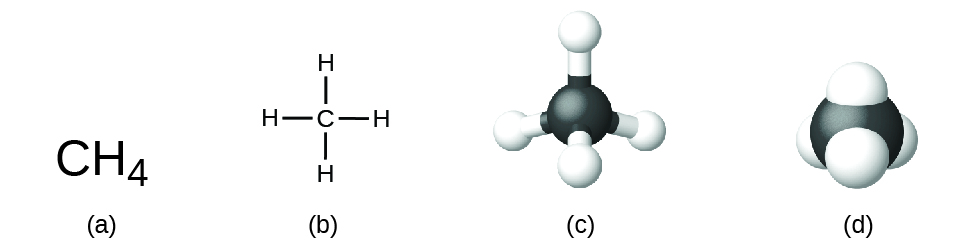
The structural formula for a compound gives the same information as its molecular formula (the types and numbers of atoms in the molecule) but also shows how the atoms are connected in the molecule. The structural formula for methane contains symbols for one C atom and four H atoms, indicating the number of atoms in the molecule ((Figure)). The lines represent bonds that hold the atoms together. (A chemical bond is an attraction between atoms or ions that holds them together in a molecule or a crystal.) We will discuss chemical bonds and see how to predict the arrangement of atoms in a molecule later. For now, simply know that the lines are an indication of how the atoms are connected in a molecule. A ball-and-stick model shows the geometric arrangement of the atoms with atomic sizes not to scale, and a space-filling model shows the relative sizes of the atoms.

A methane molecule can be represented as (a) a molecular formula, (b) a structural formula, (c) a ball-and-stick model, and (d) a space-filling model. Carbon and hydrogen atoms are represented by black and white spheres, respectively.

Figure A shows C H subscript 4. Figure B shows a carbon atom that is bonded to four hydrogen atoms at right angles: one above, one to the left, one to the right, and one below. Figure C shows a 3-D, ball-and-stick model of the carbon atom bonded to four hydrogen atoms. Figure D shows a space-filling model of a carbon atom with hydrogen atoms partially embedded into the surface of the carbon atom.

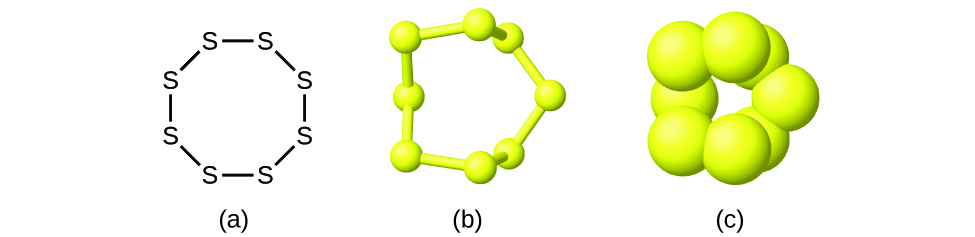
Although many elements consist of discrete, individual atoms, some exist as molecules made up of two or more atoms of the element chemically bonded together. For example, most samples of the elements hydrogen, oxygen, and nitrogen are composed of molecules that contain two atoms each (called diatomic molecules) and thus have the molecular formulas H2, O2, and N2, respectively. Other elements commonly found as diatomic molecules are fluorine (F2), chlorine (Cl2), bromine (Br2), and iodine (I2). The most common form of the element sulfur is composed of molecules that consist of eight atoms of sulfur; its molecular formula is S8 ((Figure)).

A molecule of sulfur is composed of eight sulfur atoms and is therefore written as S8. It can be represented as (a) a structural formula, (b) a ball-and-stick model, and (c) a space-filling model. Sulfur atoms are represented by yellow spheres.

Figure A shows eight sulfur atoms, symbolized with the letter S, that are bonded to each other to form an octagon. Figure B shows a 3-D, ball-and-stick model of the arrangement of the sulfur atoms. The shape is clearly not octagonal as it is represented in the structural formula. Figure C is a space-filling model that shows each sulfur atom is partially embedded into the sulfur atom it bonds with.

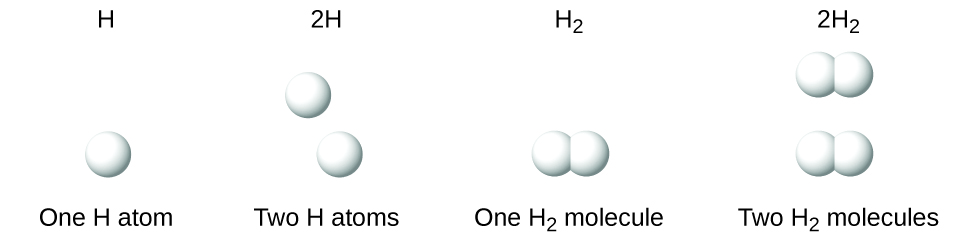
It is important to note that a subscript following a symbol and a number in front of a symbol do not represent the same thing; for example, H2 and 2H represent distinctly different species. H2 is a molecular formula; it represents a diatomic molecule of hydrogen, consisting of two atoms of the element that are chemically bonded together. The expression 2H, on the other hand, indicates two separate hydrogen atoms that are not combined as a unit. The expression 2H2 represents two molecules of diatomic hydrogen ((Figure)).

The symbols H, 2H, H2, and 2H2 represent very different entities.

This figure shows four diagrams. The diagram for H shows a single, white sphere and is labeled one H atom. The diagram for 2 H shows two white spheres that are not bonded together. It is labeled 2 H atoms. The diagram for H subscript 2 shows two white spheres bonded together. It is labeled one H subscript 2 molecule. The diagram for 2 H subscript 2 shows two sets of bonded, white spheres. It is labeled 2 H subscript 2 molecules.

Compounds are formed when two or more elements chemically combine, resulting in the formation of bonds. For example, hydrogen and oxygen can react to form water, and sodium and chlorine can react to form table salt. We sometimes describe the composition of these compounds with an empirical formula, which indicates the types of atoms present and the simplest whole-number ratio of the number of atoms (or ions) in the compound. For example, titanium dioxide (used as pigment in white paint and in the thick, white, blocking type of sunscreen) has an empirical formula of TiO2. This identifies the elements titanium (Ti) and oxygen (O) as the constituents of titanium dioxide, and indicates the presence of twice as many atoms of the element oxygen as atoms of the element titanium ((Figure)).

(a) The white compound titanium dioxide provides effective protection from the sun. (b) A crystal of titanium dioxide, TiO2, contains titanium and oxygen in a ratio of 1 to 2. The titanium atoms are gray and the oxygen atoms are red. (credit a: modification of work by “osseous”/Flickr)

Figure A shows a photo of a person applying suntan lotion to his or her lower leg. Figure B shows a 3-D ball-and-stick model of the molecule titanium dioxide, which involves a complicated interlocking of many titanium and oxygen atoms. The titanium atoms in the molecule are shown as silver spheres and the oxygen atoms are shown as red spheres. There are twice as many oxygen atoms as titanium atoms in the molecule.

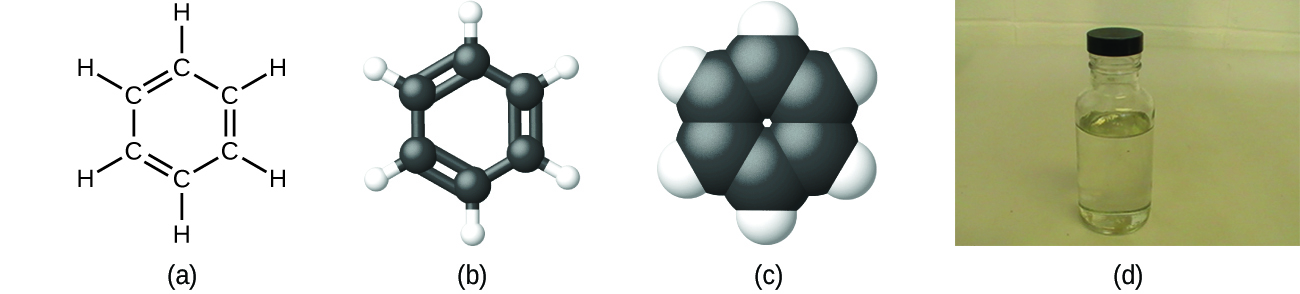
As discussed previously, we can describe a compound with a molecular formula, in which the subscripts indicate the actual numbers of atoms of each element in a molecule of the compound. In many cases, the molecular formula of a substance is derived from experimental determination of both its empirical formula and its molecular mass (the sum of atomic masses for all atoms composing the molecule). For example, it can be determined experimentally that benzene contains two elements, carbon (C) and hydrogen (H), and that for every carbon atom in benzene, there is one hydrogen atom. Thus, the empirical formula is CH. An experimental determination of the molecular mass reveals that a molecule of benzene contains six carbon atoms and six hydrogen atoms, so the molecular formula for benzene is C6H6 ((Figure)).

Benzene, C6H6, is produced during oil refining and has many industrial uses. A benzene molecule can be represented as (a) a structural formula, (b) a ball-and-stick model, and (c) a space-filling model. (d) Benzene is a clear liquid. (credit d: modification of work by Sahar Atwa)

Figure A shows that benzene is composed of six carbons shaped like a hexagon. Every other bond between the carbon atoms is a double bond. Each carbon also has a single bonded hydrogen atom. Figure B shows a 3-D, ball-and-stick drawing of benzene. The six carbon atoms are black spheres while the six hydrogen atoms are smaller, white spheres. Figure C is a space-filling model of benzene which shows that most of the interior space is occupied by the carbon atoms. The hydrogen atoms are embedded in the outside surface of the carbon atoms. Figure d shows a small vial filled with benzene which appears to be clear.

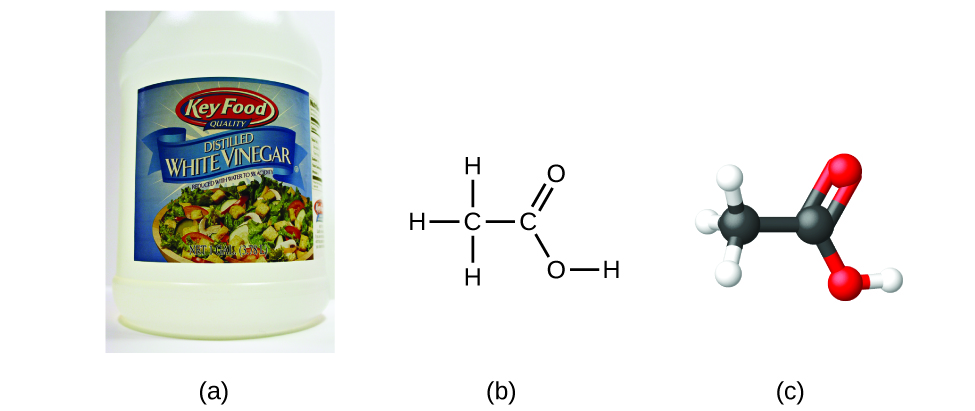
If we know a compound’s formula, we can easily determine the empirical formula. (This is somewhat of an academic exercise; the reverse chronology is generally followed in actual practice.) For example, the molecular formula for acetic acid, the component that gives vinegar its sharp taste, is C2H4O2. This formula indicates that a molecule of acetic acid ((Figure)) contains two carbon atoms, four hydrogen atoms, and two oxygen atoms. The ratio of atoms is 2:4:2. Dividing by the lowest common denominator (2) gives the simplest, whole-number ratio of atoms, 1:2:1, so the empirical formula is CH2O. Note that a molecular formula is always a whole-number multiple of an empirical formula.

(a) Vinegar contains acetic acid, C2H4O2, which has an empirical formula of CH2O. It can be represented as (b) a structural formula and (c) as a ball-and-stick model. (credit a: modification of work by “HomeSpot HQ”/Flickr)

Figure A shows a jug of distilled, white vinegar. Figure B shows a structural formula for acetic acid which contains two carbon atoms connected by a single bond. The left carbon atom forms single bonds with three hydrogen atoms. The right carbon atom forms a double bond with an oxygen atom. The right carbon atom also forms a single bond with an oxygen atom. This oxygen forms a single bond with a hydrogen atom. Figure C shows a 3-D ball-and-stick model of acetic acid.

Empirical and Molecular Formulas Molecules of glucose (blood sugar) contain 6 carbon atoms, 12 hydrogen atoms, and 6 oxygen atoms. What are the molecular and empirical formulas of glucose?

Solution The molecular formula is C6H12O6 because one molecule actually contains 6 C, 12 H, and 6 O atoms. The simplest whole-number ratio of C to H to O atoms in glucose is 1:2:1, so the empirical formula is CH2O.

Check Your Learning A molecule of metaldehyde (a pesticide used for snails and slugs) contains 8 carbon atoms, 16 hydrogen atoms, and 4 oxygen atoms. What are the molecular and empirical formulas of metaldehyde?

Answer:

Molecular formula, C8H16O4; empirical formula, C2H4O

Lee Cronin

What is it that chemists do? According to Lee Cronin ((Figure)), chemists make very complicated molecules by “chopping up” small molecules and “reverse engineering” them. He wonders if we could “make a really cool universal chemistry set” by what he calls “app-ing” chemistry. Could we “app” chemistry?

In a 2012 TED talk, Lee describes one fascinating possibility: combining a collection of chemical “inks” with a 3D printer capable of fabricating a reaction apparatus (tiny test tubes, beakers, and the like) to fashion a “universal toolkit of chemistry.” This toolkit could be used to create custom-tailored drugs to fight a new superbug or to “print” medicine personally configured to your genetic makeup, environment, and health situation. Says Cronin, “What Apple did for music, I’d like to do for the discovery and distribution of prescription drugs.”1 View his full talk at the TED website.

Chemist Lee Cronin has been named one of the UK’s 10 most inspirational scientists. The youngest chair at the University of Glasgow, Lee runs a large research group, collaborates with many scientists worldwide, has published over 250 papers in top scientific journals, and has given more than 150 invited talks. His research focuses on complex chemical systems and their potential to transform technology, but also branches into nanoscience, solar fuels, synthetic biology, and even artificial life and evolution. (credit: image courtesy of Lee Cronin)

This is a photo of chemist Lee Cronin.

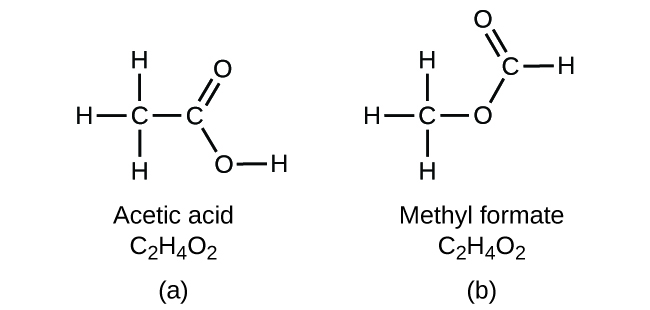
It is important to be aware that it may be possible for the same atoms to be arranged in different ways: Compounds with the same molecular formula may have different atom-to-atom bonding and therefore different structures. For example, could there be another compound with the same formula as acetic acid, C2H4O2? And if so, what would be the structure of its molecules?

If you predict that another compound with the formula C2H4O2 could exist, then you demonstrated good chemical insight and are correct. Two C atoms, four H atoms, and two O atoms can also be arranged to form a methyl formate, which is used in manufacturing, as an insecticide, and for quick-drying finishes. Methyl formate molecules have one of the oxygen atoms between the two carbon atoms, differing from the arrangement in acetic acid molecules. Acetic acid and methyl formate are examples of isomers—compounds with the same chemical formula but different molecular structures ((Figure)). Note that this small difference in the arrangement of the atoms has a major effect on their respective chemical properties. You would certainly not want to use a solution of methyl formate as a substitute for a solution of acetic acid (vinegar) when you make salad dressing.

Molecules of (a) acetic acid and methyl formate (b) are structural isomers; they have the same formula (C2H4O2) but different structures (and therefore different chemical properties).

Figure A shows a structural diagram of acetic acid, C subscript 2 H subscript 4 O subscript 2. Acetic acid contains two carbon atoms connected by a single bond. The left carbon atom forms single bonds with three hydrogen atoms. The carbon on the right forms a double bond with an oxygen atom. The right carbon atom also forms a single bond to an oxygen atom which forms a single bond with a hydrogen atom. Figure B shows a structural diagram of methyl formate, C subscript 2 H subscript 4 O subscript 2. This molecule contains a carbon atom which forms single bonds with three hydrogen atoms, and a single bond with an oxygen atom. The oxygen atom forms a single bond with another carbon atom which forms a double bond with another oxygen atom and a single bond with a hydrogen atom.

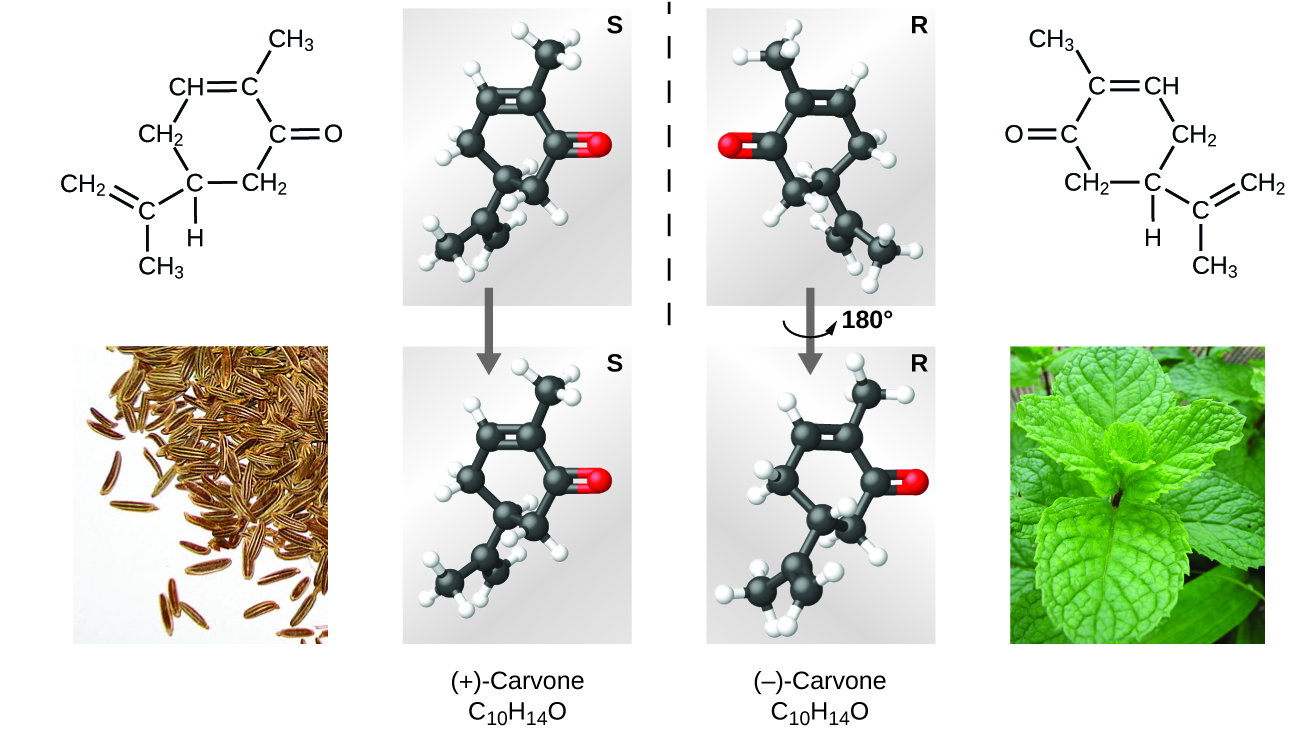
Many types of isomers exist ((Figure)). Acetic acid and methyl formate are structural isomers, compounds in which the molecules differ in how the atoms are connected to each other. There are also various types of spatial isomers, in which the relative orientations of the atoms in space can be different. For example, the compound carvone (found in caraway seeds, spearmint, and mandarin orange peels) consists of two isomers that are mirror images of each other. S-(+)-carvone smells like caraway, and R-(−)-carvone smells like spearmint.

Molecules of carvone are spatial isomers; they only differ in the relative orientations of the atoms in space. (credit bottom left: modification of work by “Miansari66”/Wikimedia Commons; credit bottom right: modification of work by Forest & Kim Starr)

The top left portion of this 2 row, 4 column figure shows a structural diagram of positive carvone, C subscript 10 H subscript 14 O. This molecule has a carbon atom which forms a double bond with a C H subscript 2 group and a C H subscript 3 group. The carbon atom also forms a single bond with another carbon atom which is part of a ring. This carbon atom, being part of the ring, forms single bonds with a hydrogen atom, a C H subscript 2 group, and a C H subscript 2 group. The first C H subscript two group forms a single bond with C H which forms a double bond with a carbon atom. This carbon atom forms a single bond with a C H subscript 3 group. The carbon atom forming part of the ring forms a single bond with a carbon atom which forms a double bond with an oxygen atom and a single bond with a C H subscript 2 group to complete the ring. Below the structural diagram of carvone is a photo of caraway seeds. Column 2 contains identical ball and stick representations of the structural diagram in the top left position. The top right portions of these images each contains the letter “S” and there is an arrow pointing downward from the top image to the bottom image. Columns 3 and 4 are representations of negative carvone. The top row in column three depicts a mirrored image of the ball and stick structure to its left, reflected across the y axis. There is a downward pointing arrow to the image below, which is the same structure rotated counter clockwise 180 degrees. Both images in column 3 have an “R” in the top right corner. The image in the first row of column 4 is the same as the lewis structure in the first row of column 1, reflected across the y axis. Below this negative carvone structural diagram is a photo of spearmint leaves.

The Mole

The identity of a substance is defined not only by the types of atoms or ions it contains, but by the quantity of each type of atom or ion. For example, water, H2O, and hydrogen peroxide, H2O2, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, we possess sophisticated instruments that allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for amount of substances, the mole, which remains indispensable in modern chemical science.

The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a sample of matter. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property, bulk mass, and an extremely important fundamental property, number of atoms, molecules, and so forth. A mole of substance is that amount in which there are 6.02214076 × 1023 discrete entities (atoms or molecules). This large number is a fundamental constant known as Avogadro’s number (NA) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being 6.022 \(×\) 1023/mol.

Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol) (see (Figure)).

Each sample contains 6.022 \(×\) 1023 atoms —1.00 mol of atoms. From left to right (top row): 65.4 g zinc, 12.0 g carbon, 24.3 g magnesium, and 63.5 g copper. From left to right (bottom row): 32.1 g sulfur, 28.1 g silicon, 207 g lead, and 118.7 g tin. (credit: modification of work by Mark Ott)

This figure contains eight different substances displayed on white circles. The amount of each substance is visibly different.

The molar mass of any substance is numerically equivalent to its atomic or formula weight in amu. Per the amu definition, a single 12C atom weighs 12 amu (its atomic mass is 12 amu). A mole of 12C atoms weighs 12 g (its molar mass is 12 g/mol). This relationship holds for all elements, since their atomic masses are measured relative to that of the amu-reference substance, 12C. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu ((Figure)).

Each sample contains 6.02 \(×\) 1023 molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2 g of C8H17OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI2 (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH3OH (methanol, formula mass 32.0 amu) and 256.5 g of S8 (sulfur, formula mass 256.5 amu). (credit: Sahar Atwa)

This photo shows two vials filled with a colorless liquid. It also shows two bowls: one filled with an off-white powder and one filled with a bright red powder.

Element Average Atomic Mass (amu) Molar Mass (g/mol) Atoms/Mole
C 12.01 12.01 6.022 \(×\) 1023
H 1.008 1.008 6.022 \(×\) 1023
O 16.00 16.00 6.022 \(×\) 1023
Na 22.99 22.99 6.022 \(×\) 1023
Cl 35.45 35.45 6.022 \(×\) 1023

While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g (see (Figure)). Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

The number of molecules in a single droplet of water is roughly 100 billion times greater than the number of people on earth. (credit: “tanakawho”/Wikimedia commons)

A close-up photo of a water droplet on a leaf is shown. The water droplet is not perfectly spherical.

The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.

Deriving Moles from Grams for an Element According to nutritional guidelines from the US Department of Agriculture, the estimated average requirement for dietary potassium is 4.7 g. What is the estimated average requirement of potassium in moles?

Solution The mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.

The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Mass of K atoms ( g )” while the one on the right contains the phrase, “Moles of K atoms ( mol ).” There is a phrase under the arrow that says, “Divide by molar mass (g / mol).”

The factor-label method supports this mathematical approach since the unit “g” cancels and the answer has units of “mol:”

\(4.7\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}\phantom{\rule{0.2em}{0ex}}\text{K}\phantom{\rule{0.2em}{0ex}}\left(\frac{\text{mol K}}{39.10\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}0.12\phantom{\rule{0.2em}{0ex}}\text{mol K}\)

The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation, since it is a bit greater than 0.1 mol.

Check Your Learning Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?

Answer:

0.360 mol

Deriving Grams from Moles for an Element A liter of air contains 9.2 \(×\) 10−4 mol argon. What is the mass of Ar in a liter of air?

Solution The molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10−3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Moles of A r atoms ( mol )” while the one on the right contains the phrase, “Mass of A r atoms ( g ).” There is a phrase under the arrow that says “Multiply by molar mass ( g / mol ).”

In this case, logic dictates (and the factor-label method supports) multiplying the provided amount (mol) by the molar mass (g/mol):

\(9.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}\text{Ar}\phantom{\rule{0.2em}{0ex}}\left(\frac{39.95\phantom{\rule{0.2em}{0ex}}\text{g}}{\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}\text{Ar}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}0.037\phantom{\rule{0.2em}{0ex}}\text{g Ar}\)

The result is in agreement with our expectations, around 0.04 g Ar.

Check Your Learning What is the mass of 2.561 mol of gold?

Answer:

504.4 g

Deriving Number of Atoms from Mass for an Element Copper is commonly used to fabricate electrical wire ((Figure)). How many copper atoms are in 5.00 g of copper wire?

Copper wire is composed of many, many atoms of Cu. (credit: Emilian Robert Vicol)

A close-up photo of a spool of copper wire is shown.

Solution The number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to number of Cu atoms:

A diagram of three boxes connected by a right-facing arrow in between each is shown. The box on the left contains the phrase, “Mass of C u atoms ( g ),” the middle box reads, “Moles of C u atoms ( mol ),” while the one on the right contains the phrase, “Number of C u atoms.” There is a phrase under the left arrow that says “Divide by molar mass (g / mol),” and under the right arrow it states, “Multiply by Avogadro’s number ( mol superscript negative one ).”

Considering that the provided sample mass (5.00 g) is a little less than one-tenth the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields:

\(5.00\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}\phantom{\rule{0.2em}{0ex}}\text{Cu}\phantom{\rule{0.2em}{0ex}}\left(\frac{\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}\text{Cu}}{63.55\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}}\right)\left(\frac{6.022\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{23}\phantom{\rule{0.2em}{0ex}}\text{atoms}}{\overline{)\text{mol}}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}4.74\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{22}\text{atoms of copper}\)

The factor-label method yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.

Check Your Learning A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?

Answer:

4.586 \(×\) 1022 Au atoms

Deriving Moles from Grams for a Compound Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?

Solution We can derive the number of moles of a compound from its mass following the same procedure we used for an element in (Figure):

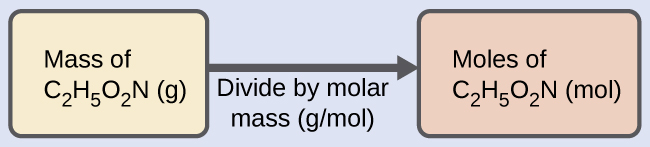
A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Mass of C subscript 2 H subscript 5 O subscript 2 N ( g )” while the box on the right contains the phrase, “Moles of C subscript 2 H subscript 5 O subscript 2 N ( mol ).” There is a phrase under the arrow that says “Divide by molar mass (g / mol).”

The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:

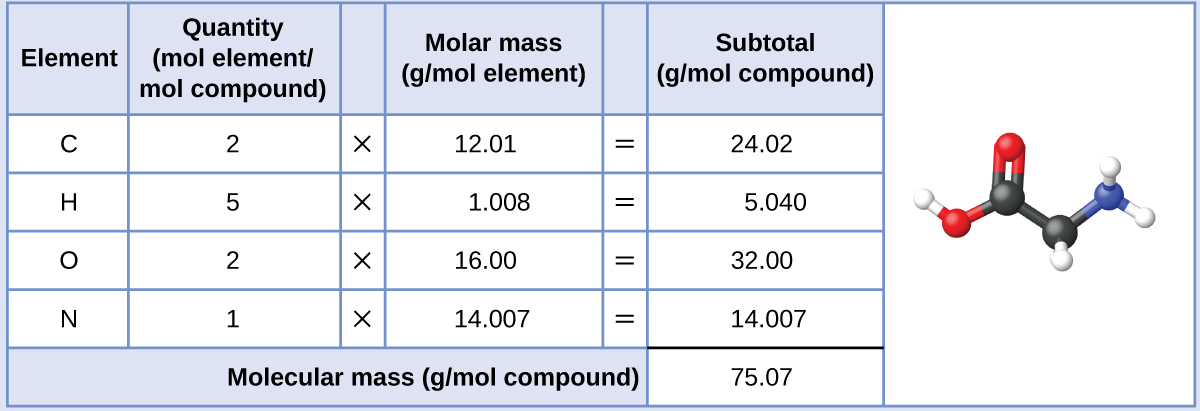
A table is shown that is made up of six columns and six rows. The header row reads: “Element,” “Quantity (mol element / mol compound,” a blank space, “Molar mass (g / mol element),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” “N,” and a merged cell. The merged cell runs the width of the first five columns. The second column contains the numbers “2,” “5,” “2,” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” “16.00,” and “14.007” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “24.02,” “5.040,” “32.00,” “14.007,” and “75.07.” There is a thick black line under the number 14.007. The merged cell under the first five columns reads “Molar mass (g / mol compound). There is a ball-and-stick drawing to the right of this table. It shows a black sphere that forms a double bond with a slightly smaller red sphere, a single bond with another red sphere, and a single bond with another black sphere. The red sphere that forms a single bond with the black sphere also forms a single bond with a smaller, white sphere. The second black sphere forms a single bond with a smaller, white sphere and a smaller blue sphere. The blue sphere forms a single bond with two smaller, white spheres each.

The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:

\(28.35\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}\phantom{\rule{0.2em}{0ex}}\text{glycine}\phantom{\rule{0.2em}{0ex}}\left(\frac{\text{mol glycine}}{75.07\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}0.378\phantom{\rule{0.2em}{0ex}}\text{mol glycine}\)

This result is consistent with our rough estimate.

Check Your Learning How many moles of sucrose, C12H22O11, are in a 25-g sample of sucrose?

Answer:

0.073 mol

Deriving Grams from Moles for a Compound Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 \(×\) 10−4 mol. What is the mass of this allowance in grams?

Solution As for elements, the mass of a compound can be derived from its molar amount as shown:

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Moles of vitamin C ( mol )” while the one the right contains the phrase, “Mass of vitamin C ( g )”. There is a phrase under the arrow that says “Multiply by molar mass (g / mol).”

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:

\(1.42\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}\text{vitamin C}\phantom{\rule{0.2em}{0ex}}\left(\frac{176.124\phantom{\rule{0.2em}{0ex}}\text{g}}{\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}\text{vitamin C}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}0.0250\phantom{\rule{0.2em}{0ex}}\text{g vitamin C}\)

This is consistent with the anticipated result.

Check Your Learning What is the mass of 0.443 mol of hydrazine, N2H4?

Answer:

14.2 g

Deriving the Number of Atoms and Molecules from the Mass of a Compound A packet of an artificial sweetener contains 40.0 mg of saccharin (C7H5NO3S), which has the structural formula:

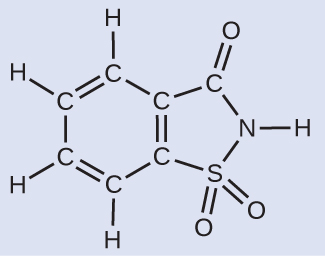
A diagram of a molecule is shown that is made up of two ring structures attached together. The left ring is hexagonal in shape with C atoms at each point of the ring and alternating single and double bonds. A double bond occurs between the C atom at the top vertex of the hexagon and the C atom down and to the left of it. The C atoms on the left, top, and bottom of the structure form a single bond to an H atom each. The two right C atoms make up one side of a pentagon and the other points of the pentagon are made up of a C atom, an N atom, and an S atom if read clockwise. The C atom forms a double bond with an O atom. The N atom forms a single bond with an H atom. The S atom forms two double bonds to two O atoms.

Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0-mg (0.0400-g) sample of saccharin? How many carbon atoms are in the same sample?

Solution The number of molecules in a given mass of compound is computed by first deriving the number of moles, as demonstrated in (Figure), and then multiplying by Avogadro’s number:

A diagram of three boxes connected by a right-facing arrow in between each is shown. The box on the left contains the phrase, “Mass of C subscript seven H subscript five N O subscript three S ( g ),” the middle box reads, “Moles of C subscript seven H subscript five N O subscript three S ( mol ),” while the one on the right contains the phrase, “Number of C subscript seven H subscript five N O subscript three S molecules.” There is a phrase under the left arrow that says, “Divide by molar mass (g / mol),” and under the right arrow it states, “Multiply by Avogadro’s number ( mol superscript negative one).”

Using the provided mass and molar mass for saccharin yields:

\(\begin{array}{}\\ \\ 0.0400\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S}\phantom{\rule{0.2em}{0ex}}\left(\frac{\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S}}{183.18\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S}}\right)\left(\frac{6.022\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{23}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S}\phantom{\rule{0.2em}{0ex}}\text{molecules}}{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{mol}}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S}}\right)\\ =\phantom{\rule{0.2em}{0ex}}1.31\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{20}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S}\phantom{\rule{0.2em}{0ex}}\text{molecules}\end{array}\)

The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is:

\(1.31\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{20}\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S molecules}\phantom{\rule{0.2em}{0ex}}\left(\frac{7\phantom{\rule{0.2em}{0ex}}\text{C atoms}}{1\phantom{\rule{0.2em}{0ex}}{\text{C}}_{7}{\text{H}}_{5}{\text{NO}}_{3}\text{S molecule}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}9.17\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{20}\phantom{\rule{0.2em}{0ex}}\text{C atoms}\)

Check Your Learning How many C4H10 molecules are contained in 9.213 g of this compound? How many hydrogen atoms?

Answer:

9.545 \(×\) 1022 molecules C4 H10; 9.545 \(×\) 1023 atoms H

Counting Neurotransmitter Molecules in the Brain

The brain is the control center of the central nervous system ((Figure)). It sends and receives signals to and from muscles and other internal organs to monitor and control their functions; it processes stimuli detected by sensory organs to guide interactions with the external world; and it houses the complex physiological processes that give rise to our intellect and emotions. The broad field of neuroscience spans all aspects of the structure and function of the central nervous system, including research on the anatomy and physiology of the brain. Great progress has been made in brain research over the past few decades, and the BRAIN Initiative, a federal initiative announced in 2013, aims to accelerate and capitalize on these advances through the concerted efforts of various industrial, academic, and government agencies (more details available at www.whitehouse.gov/share/brain-initiative).

(a) A typical human brain weighs about 1.5 kg and occupies a volume of roughly 1.1 L. (b) Information is transmitted in brain tissue and throughout the central nervous system by specialized cells called neurons (micrograph shows cells at 1600× magnification).

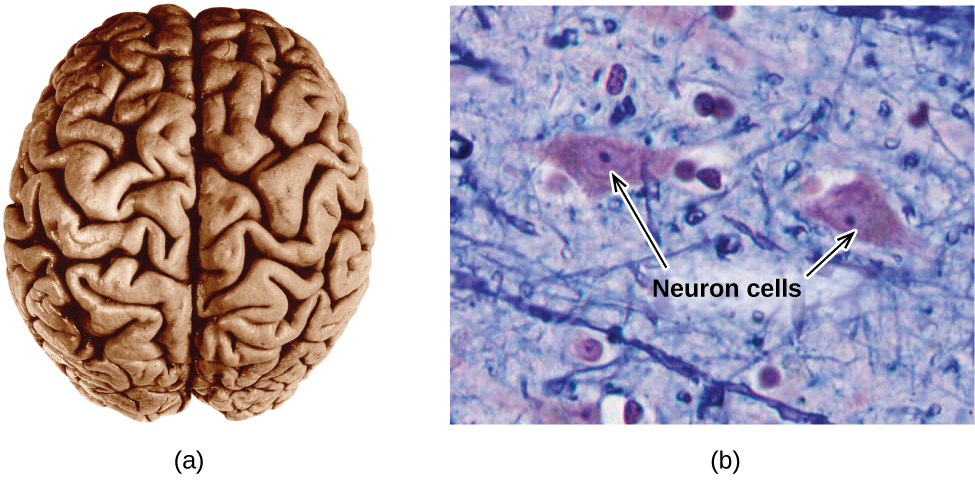
Two pictures are shown. The left picture shows the human brain. The right picture is a microscopic image that depicts two large irregularly shaped masses in a field of threadlike material interspersed with smaller, relatively round masses. The two larger masses are labeled with arrows and the phrase “Neuron cells.”

Specialized cells called neurons transmit information between different parts of the central nervous system by way of electrical and chemical signals. Chemical signaling occurs at the interface between different neurons when one of the cells releases molecules (called neurotransmitters) that diffuse across the small gap between the cells (called the synapse) and bind to the surface of the other cell. These neurotransmitter molecules are stored in small intracellular structures called vesicles that fuse to the cell wall and then break open to release their contents when the neuron is appropriately stimulated. This process is called exocytosis (see (Figure)). One neurotransmitter that has been very extensively studied is dopamine, C8H11NO2. Dopamine is involved in various neurological processes that impact a wide variety of human behaviors. Dysfunctions in the dopamine systems of the brain underlie serious neurological diseases such as Parkinson’s and schizophrenia.

(a) Chemical signals are transmitted from neurons to other cells by the release of neurotransmitter molecules into the small gaps (synapses) between the cells. (b) Dopamine, C8H11NO2, is a neurotransmitter involved in a number of neurological processes.

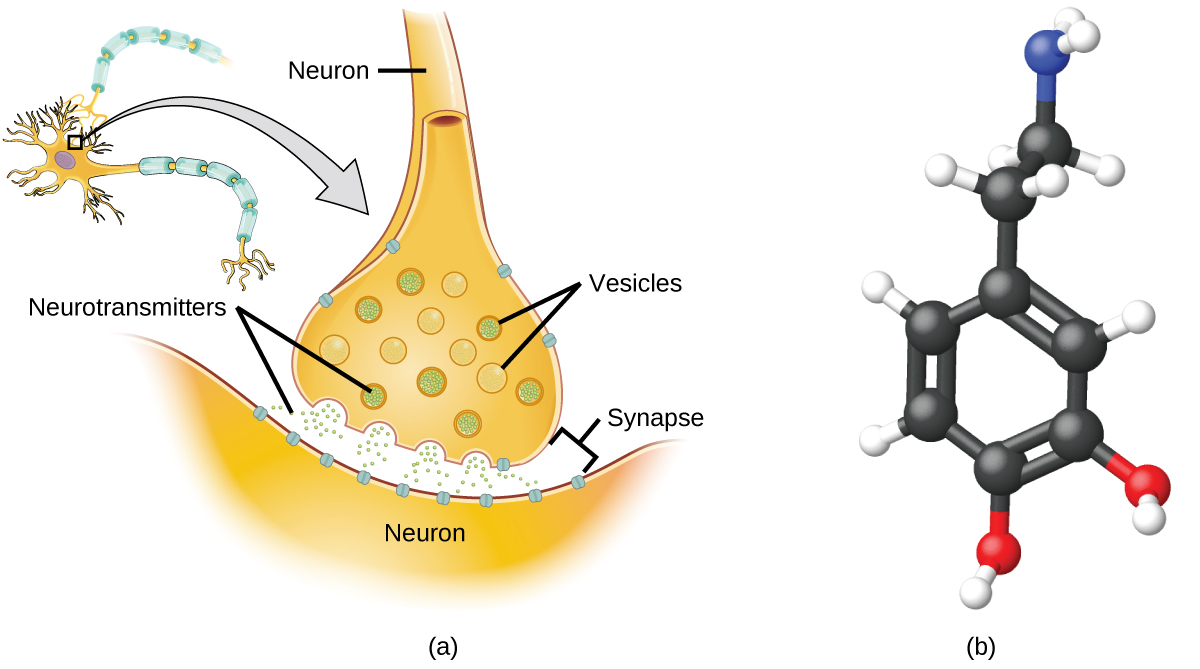
Two diagrams are shown. In the upper left corner of the left diagram, an oval with a darkened center that has five short, branching appendages and one long tail-like appendage is shown and connected by an arrow to another image. This image depicts a close-up view of the oval section and its interaction with the tail-like portion of a similar structure. The close up view is composed of a narrow tube labeled “neuron” leading down to a bulbous base that holds thirteen circles filled with small dots. These circles are labeled “vesicles.” The base of the bulbous structure is next to a curved object labeled “neuron” and very small dots are emerging from the bulb’s base and flowing toward the curved structure. The gap in between the two structures is labeled “synapse,” and the small dots are labeled “neurotransmitters.” The diagram on the right depicts a molecule composed of six black spheres connected by alternating double and single bonds in a hexagonal ring with other spheres attached to it. Three of the black spheres are connected to one smaller, white sphere each. Two of the black balls are connected to a smaller red sphere each. Each red sphere is connected to a smaller, white sphere. One black sphere is connected to another black sphere. It is connected to two smaller, white spheres and another black sphere. This second black sphere is connected to two smaller white spheres, and a slightly smaller blue sphere. The blue sphere is connected to two smaller, white spheres.

One important aspect of the complex processes related to dopamine signaling is the number of neurotransmitter molecules released during exocytosis. Since this number is a central factor in determining neurological response (and subsequent human thought and action), it is important to know how this number changes with certain controlled stimulations, such as the administration of drugs. It is also important to understand the mechanism responsible for any changes in the number of neurotransmitter molecules released—for example, some dysfunction in exocytosis, a change in the number of vesicles in the neuron, or a change in the number of neurotransmitter molecules in each vesicle.

Significant progress has been made recently in directly measuring the number of dopamine molecules stored in individual vesicles and the amount actually released when the vesicle undergoes exocytosis. Using miniaturized probes that can selectively detect dopamine molecules in very small amounts, scientists have determined that the vesicles of a certain type of mouse brain neuron contain an average of 30,000 dopamine molecules per vesicle (about \(5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-20}\) mol or 50 zmol). Analysis of these neurons from mice subjected to various drug therapies shows significant changes in the average number of dopamine molecules contained in individual vesicles, increasing or decreasing by up to three-fold, depending on the specific drug used. These studies also indicate that not all of the dopamine in a given vesicle is released during exocytosis, suggesting that it may be possible to regulate the fraction released using pharmaceutical therapies.2

Key Concepts and Summary

A molecular formula uses chemical symbols and subscripts to indicate the exact numbers of different atoms in a molecule or compound. An empirical formula gives the simplest, whole-number ratio of atoms in a compound. A structural formula indicates the bonding arrangement of the atoms in the molecule. Ball-and-stick and space-filling models show the geometric arrangement of atoms in a molecule. Isomers are compounds with the same molecular formula but different arrangements of atoms. A convenient amount unit for expressing very large numbers of atoms or molecules is the mole. Experimental measurements have determined the number of entities composing 1 mole of substance to be 6.022 \(×\) 1023, a quantity called Avogadro’s number. The mass in grams of 1 mole of substance is its molar mass.

Chemistry End of Chapter Exercises

Explain why the symbol for an atom of the element oxygen and the formula for a molecule of oxygen differ.

The symbol for the element oxygen, O, represents both the element and one atom of oxygen. A molecule of oxygen, O2, contains two oxygen atoms; the subscript 2 in the formula must be used to distinguish the diatomic molecule from two single oxygen atoms.

Explain why the symbol for the element sulfur and the formula for a molecule of sulfur differ.

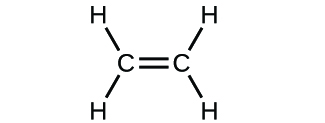
Write the molecular and empirical formulas of the following compounds:

(a)

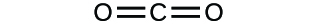
Figure A shows a carbon atom that forms two, separate double bonds with two oxygen atoms.


 (b)

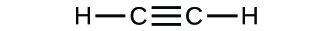
Figure B shows a hydrogen atom which forms a single bond with a carbon atom. The carbon atom forms a triple bond with another carbon atom. The second carbon atom forms a single bond with a hydrogen atom.


 (c)

Figure C shows a carbon atom forming a double bond with another carbon atom. Each carbon atom forms a single bond with two hydrogen atoms.


 (d)

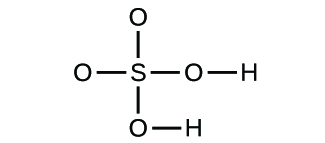
Figure D shows a sulfur atom forming single bonds with four oxygen atoms. Two of the oxygen atoms form a single bond with a hydrogen atom.

(a) molecular CO2, empirical CO2; (b) molecular C2H2, empirical CH; (c) molecular C2H4, empirical CH2; (d) molecular H2SO4, empirical H2SO4

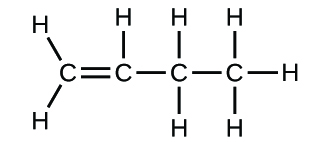
Write the molecular and empirical formulas of the following compounds:

(a)

Figure A shows a structural diagram of four carbon atoms bonded together into a chain. The two carbon atoms on the left form a double bond with each other. All of the remaining carbon atoms form single bonds with each other. The leftmost carbon also forms single bonds with two hydrogen. The second carbon in the chain forms a single bond with a hydrogen atom. The third carbon in the chain forms a single bond with two hydrogen atoms each. The rightmost carbon forms a single bond with three hydrogen atoms each.


 (b)

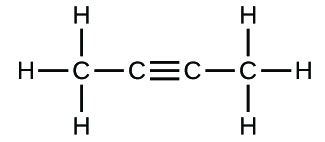
Figure B shows a structural diagram of a molecule that has a chain of four carbon atoms. The leftmost carbon atom forms a single bond with three hydrogen atoms each and single bond with the second carbon atom. The second carbon atom forms a triple bond with the third carbon atom. The third carbon atom forms a single bond to the fourth carbon atom. The fourth carbon atom forms a single bond to three hydrogen atoms each.


 (c)

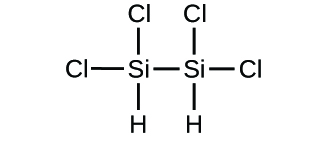
Figure C shows a structural diagram of two silicon atoms are bonded together with a single bond. Each of the silicon atoms form single bonds to two chlorine atoms each and one hydrogen atom.


 (d)

Figure D shows a structural diagram of a phosphorus atom that forms a single bond to four oxygen atoms each. Three of the oxygen atoms each have a single bond to a hydrogen atom.

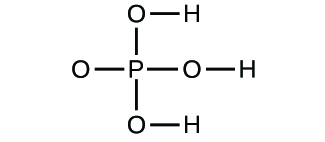
Determine the empirical formulas for the following compounds:

(a) caffeine, C8H10N4O2

(b) fructose, C12H22O11

(c) hydrogen peroxide, H2O2

(d) glucose, C6H12O6

(e) ascorbic acid (vitamin C), C6H8O6

(a) C4H5N2O; (b) C12H22O11; (c) HO; (d) CH2O; (e) C3H4O3

Determine the empirical formulas for the following compounds:

(a) acetic acid, C2H4O2

(b) citric acid, C6H8O7

(c) hydrazine, N2H4

(d) nicotine, C10H14N2

(e) butane, C4H10

Write the empirical formulas for the following compounds:

(a)

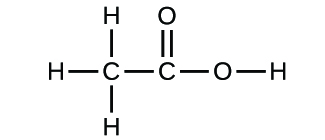
Figure A shows a structural diagram of two carbon atoms that form a single bond with each other. The left carbon atom forms single bonds with hydrogen atoms each. The right carbon forms a double bond to an oxygen atom. The right carbon also forms a single bonded to another oxygen atom. This oxygen atom also forms a single bond to a hydrogen atom.


 (b)

Figure B shows a structural diagram containing a leftmost carbon that forms single bonds to three hydrogen atoms each. This leftmost carbon also forms a single bond to a second carbon atom. The second carbon atom forms a double bond with an oxygen atom. The second carbon also forms a single bond to a second oxygen atom. This oxygen atom forms a single bond to a third carbon atom. This third carbon atom forms single bonds with two hydrogen atoms each as well as a single bond with another carbon atom. The rightmost carbon atom forms a single bond with three hydrogen atoms each.

(a) CH2O; (b) C2H4O

Open the Build a Molecule simulation and select the “Larger Molecules” tab. Select an appropriate atom’s “Kit” to build a molecule with two carbon and six hydrogen atoms. Drag atoms into the space above the “Kit” to make a molecule. A name will appear when you have made an actual molecule that exists (even if it is not the one you want). You can use the scissors tool to separate atoms if you would like to change the connections. Click on “3D” to see the molecule, and look at both the space-filling and ball-and-stick possibilities.

(a) Draw the structural formula of this molecule and state its name.

(b) Can you arrange these atoms in any way to make a different compound?

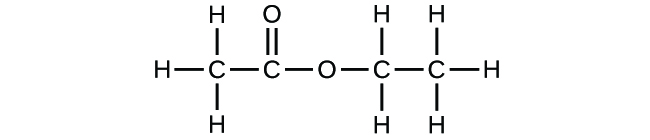
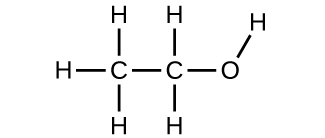
Use the Build a Molecule simulation to repeat (Figure), but build a molecule with two carbons, six hydrogens, and one oxygen.

(a) Draw the structural formula of this molecule and state its name.

(b) Can you arrange these atoms to make a different molecule? If so, draw its structural formula and state its name.

(c) How are the molecules drawn in (a) and (b) the same? How do they differ? What are they called (the type of relationship between these molecules, not their names)?

(a) ethanol

A Lewis Structure is shown. An oxygen atom is bonded to a hydrogen atom and a carbon atom. The carbon atom is bonded to two hydrogen atoms and another carbon atom. That carbon atom is bonded to three more hydrogen atoms. There are a total of two carbon atoms, six hydrogen atoms, and one oxygen atoms.

(b) methoxymethane, more commonly known as dimethyl ether

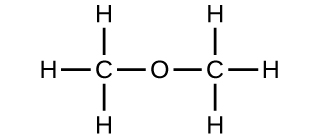
A Lewis Structure is shown. An oxygen atom is bonded to two carbon atoms. Each carbon atom is bonded to three different hydrogen atoms. There are a total of two carbon atoms, six hydrogen atoms, and one oxygen atom.

(c) These molecules have the same chemical composition (types and number of atoms) but different chemical structures. They are structural isomers.

Use the Build a Molecule simulation to repeat (Figure), but build a molecule with three carbons, seven hydrogens, and one chlorine.

(a) Draw the structural formula of this molecule and state its name.

(b) Can you arrange these atoms to make a different molecule? If so, draw its structural formula and state its name.

(c) How are the molecules drawn in (a) and (b) the same? How do they differ? What are they called (the type of relationship between these molecules, not their names)?

Write a sentence that describes how to determine the number of moles of a compound in a known mass of the compound if we know its molecular formula.

Use the molecular formula to find the molar mass; to obtain the number of moles, divide the mass of compound by the molar mass of the compound expressed in grams.

Compare 1 mole of H2, 1 mole of O2, and 1 mole of F2.

(a) Which has the largest number of molecules? Explain why.

(b) Which has the greatest mass? Explain why.

Which contains the greatest mass of oxygen: 0.75 mol of ethanol (C2H5OH), 0.60 mol of formic acid (HCO2H), or 1.0 mol of water (H2O)? Explain why.

Formic acid. Its formula has twice as many oxygen atoms as the other two compounds (one each). Therefore, 0.60 mol of formic acid would be equivalent to 1.20 mol of a compound containing a single oxygen atom.

Which contains the greatest number of moles of oxygen atoms: 1 mol of ethanol (C2H5OH), 1 mol of formic acid (HCO2H), or 1 mol of water (H2O)? Explain why.

How are the molecular mass and the molar mass of a compound similar and how are they different?

The two masses have the same numerical value, but the units are different: The molecular mass is the mass of 1 molecule while the molar mass is the mass of 6.022 \(×\) 1023 molecules.

Calculate the molar mass of each of the following compounds:

(a) hydrogen fluoride, HF

(b) ammonia, NH3

(c) nitric acid, HNO3

(d) silver sulfate, Ag2SO4

(e) boric acid, B(OH)3

Calculate the molar mass of each of the following:

(a) S8

(b) C5H12

(c) Sc2(SO4)3

(d) CH3COCH3 (acetone)

(e) C6H12O6 (glucose)

(a) 256.528 g/mol; (b) 72.150 g mol−1; (c) 378.103 g mol−1; (d) 58.080 g mol−1; (e) 180.158 g mol−1

Calculate the empirical or molecular formula mass and the molar mass of each of the following minerals:

(a) limestone, CaCO3

(b) halite, NaCl

(c) beryl, Be3Al2Si6O18

(d) malachite, Cu2(OH)2CO3

(e) turquoise, CuAl6(PO4)4(OH)8(H2O)4

Calculate the molar mass of each of the following:

(a) the anesthetic halothane, C2HBrClF3

(b) the herbicide paraquat, C12H14N2Cl2

(c) caffeine, C8H10N4O2

(d) urea, CO(NH2)2

(e) a typical soap, C17H35CO2Na

(a) 197.382 g mol−1; (b) 257.163 g mol−1; (c) 194.193 g mol−1; (d) 60.056 g mol−1; (e) 306.464 g mol−1

Determine the number of moles of compound and the number of moles of each type of atom in each of the following:

(a) 25.0 g of propylene, C3H6

(b) 3.06 \(×\) 10−3 g of the amino acid glycine, C2H5NO2

(c) 25 lb of the herbicide Treflan, C13H16N2O4F (1 lb = 454 g)

(d) 0.125 kg of the insecticide Paris Green, Cu4(AsO3)2(CH3CO2)2

(e) 325 mg of aspirin, C6H4(CO2H)(CO2CH3)

Determine the mass of each of the following:

(a) 0.0146 mol KOH

(b) 10.2 mol ethane, C2H6

(c) 1.6 \(×\) 10−3 mol Na2 SO4

(d) 6.854 \(×\) 103 mol glucose, C6 H12 O6

(e) 2.86 mol Co(NH3)6Cl3

(a) 0.819 g;
 (b) 307 g;
 (c) 0.23 g;
 (d) 1.235 \(×\) 106 g (1235 kg);
 (e) 765 g

Determine the number of moles of the compound and determine the number of moles of each type of atom in each of the following:

(a) 2.12 g of potassium bromide, KBr

(b) 0.1488 g of phosphoric acid, H3PO4

(c) 23 kg of calcium carbonate, CaCO3

(d) 78.452 g of aluminum sulfate, Al2(SO4)3

(e) 0.1250 mg of caffeine, C8H10N4O2

Determine the mass of each of the following:

(a) 2.345 mol LiCl

(b) 0.0872 mol acetylene, C2H2

(c) 3.3 \(×\) 10−2 mol Na2 CO3

(d) 1.23 \(×\) 103 mol fructose, C6 H12 O6

(e) 0.5758 mol FeSO4(H2O)7

(a) 99.41 g;
 (b) 2.27 g;
 (c) 3.5 g;
 (d) 222 kg;
 (e) 160.1 g

The approximate minimum daily dietary requirement of the amino acid leucine, C6H13NO2, is 1.1 g. What is this requirement in moles?

Determine the mass in grams of each of the following:

(a) 0.600 mol of oxygen atoms

(b) 0.600 mol of oxygen molecules, O2

(c) 0.600 mol of ozone molecules, O3

(a) 9.60 g; (b) 19.2 g; (c) 28.8 g

A 55-kg woman has 7.5 \(×\) 10−3 mol of hemoglobin (molar mass = 64,456 g/mol) in her blood. How many hemoglobin molecules is this? What is this quantity in grams?

Determine the number of atoms and the mass of zirconium, silicon, and oxygen found in 0.3384 mol of zircon, ZrSiO4, a semiprecious stone.

zirconium: 2.038 \(×\) 1023 atoms; 30.87 g; silicon: 2.038 \(×\) 1023 atoms; 9.504 g; oxygen: 8.151 \(×\) 1023 atoms; 21.66 g

Determine which of the following contains the greatest mass of hydrogen: 1 mol of CH4, 0.6 mol of C6H6, or 0.4 mol of C3H8.

Determine which of the following contains the greatest mass of aluminum: 122 g of AlPO4, 266 g of Al2C16, or 225 g of Al2S3.

AlPO4: 1.000 mol
 Al2Cl6: 1.994 mol
 Al2S3: 3.00 mol

Diamond is one form of elemental carbon. An engagement ring contains a diamond weighing 1.25 carats (1 carat = 200 mg). How many atoms are present in the diamond?

The Cullinan diamond was the largest natural diamond ever found (January 25, 1905). It weighed 3104 carats (1 carat = 200 mg). How many carbon atoms were present in the stone?

3.113 \(×\) 1025 C atoms

One 55-gram serving of a particular cereal supplies 270 mg of sodium, 11% of the recommended daily allowance. How many moles and atoms of sodium are in the recommended daily allowance?

A certain nut crunch cereal contains 11.0 grams of sugar (sucrose, C12H22O11) per serving size of 60.0 grams. How many servings of this cereal must be eaten to consume 0.0278 moles of sugar?

0.865 servings, or about 1 serving.

A tube of toothpaste contains 0.76 g of sodium monofluorophosphate (Na2PO3F) in 100 mL.

(a) What mass of fluorine atoms in mg was present?

(b) How many fluorine atoms were present?

Which of the following represents the least number of molecules?

(a) 20.0 g of H2O (18.02 g/mol)

(b) 77.0 g of CH4 (16.06 g/mol)

(c) 68.0 g of CaH2 (42.09 g/mol)

(d) 100.0 g of N2O (44.02 g/mol)

(e) 84.0 g of HF (20.01 g/mol)

20.0 g H2O represents the least number of molecules since it has the least number of moles.

Footnotes

  • 1Lee Cronin, “Print Your Own Medicine,” Talk presented at TED Global 2012, Edinburgh, Scotland, June 2012.
  • 2Omiatek, Donna M., Amanda J. Bressler, Ann-Sofie Cans, Anne M. Andrews, Michael L. Heien, and Andrew G. Ewing. “The Real Catecholamine Content of Secretory Vesicles in the CNS Revealed by Electrochemical Cytometry.” Scientific Report 3 (2013): 1447, accessed January 14, 2015, doi:10.1038/srep01447.

Glossary

empirical formula
formula showing the composition of a compound given as the simplest whole-number ratio of atoms
isomers
compounds with the same chemical formula but different structures
molecular formula
formula indicating the composition of a molecule of a compound and giving the actual number of atoms of each element in a molecule of the compound.
spatial isomers
compounds in which the relative orientations of the atoms in space differ
structural formula
shows the atoms in a molecule and how they are connected
structural isomer
one of two substances that have the same molecular formula but different physical and chemical properties because their atoms are bonded differently

License

Icon for the Creative Commons Attribution 4.0 International License

Atoms First / OpenStax Copyright © 2018 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book