2.3 Common Source Amplifier
The common source amplifier is analogous to the common emitter amplifier. The prototype amplifier circuit with device model is shown in Figure 2.3.1 .
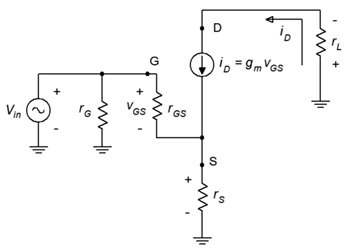
This circuit includes a swamping resistor, 𝑟𝑆 . The input signal is presented to the gate terminal while the output is taken from the drain.
Voltage Gain
An equation for the voltage gain, 𝐴𝑣, is developed as follows. First, we start with the fundamental definition, namely that voltage gain is the ratio of 𝑣𝑜𝑢𝑡 to 𝑣𝑖𝑛, and proceed by expressing these voltages in terms of their Ohm’s law equivalents.
![]()
![]()
![]()
![]()
(2.3.1)
If there is no swamping resistor, the first portion of the denominator drops out and the gain simplifies to −𝑔𝑚⋅𝑟𝐿 . The swamping resistor in the source, 𝑟𝑆, plays the same role here as it did in the BJT: it helps to stabilize the gain and reduce distortion. It does so at the expense of voltage gain.
Input Impedance
Referring back to Figure 2.3.1 , the input impedance of the amplifier will be 𝑟𝐺 in parallel with the impedance looking into the gate terminal, 𝑍𝑖𝑛(𝑔𝑎𝑡𝑒). For the non-swamped case, this will be 𝑟𝐺𝑆. At low frequencies 𝑟𝐺𝑆 is very large, well into the megohms. In most practical circuits, 𝑟𝐺 will be much lower, hence
Z_{in} = r_G || r_{GS} \approx r_G \](2.3.2)
Theoretically, for swamped amplifiers 𝑍𝑖𝑛(𝑔𝑎𝑡𝑒) will be higher than 𝑟𝐺𝑆 but this is a moot point. In either case, it is relatively easy to obtain a high input impedance, certainly much easier than it is for typical single-device BJT amplifiers.
It might be easy to become complacent and simply assume that 𝑟𝐺 sets the input impedance and that’s the end of it. This would be a mistake. As mentioned earlier, with impedances this high, we cannot ignore items such as junction capacitance. For example, for a general purpose device a typical value for 𝐶𝑖𝑠𝑠 , the total input capacitance, may be in the vicinity of 5 to 10 pF. This capacitance appears in parallel with 𝑟𝐺. If this amplifier is used for ultrasonic signals, the capacitive reactance, 𝑋𝐶, would be as low as 160 k Ω at 100 kHz. Although this is high compared to typical BJT circuits, it’s less than the 𝑅𝐺 values commonly used for biasing. At higher frequencies, the situation is even worse as 𝑋𝐶 decreases with frequency. Also, we are ignoring the Miller effect here which makes the situation even worse than even worse, so perhaps we can say that it’s even worser, which is a claim we could also make regarding the grammar of this sentence.
Output Impedance
To investigate the output impedance, we’ll refer to Figure 2.3.2 . This circuit is very similar to that of Figure 2.3.1 . The major difference is that the AC load equivalent has been split into its two components, the load itself, 𝑅𝐿, and the drain biasing resistor, 𝑅𝐷.
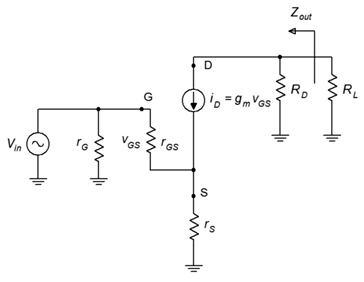
From the vantage point of 𝑅𝐿, peering back into the amplifier we see 𝑅𝐷 in parallel with the impedance at the drain. At the drain we find the current source, 𝑖𝐷 . The internal impedance of this equivalent current source is very high compared to typical values for 𝑅𝐷 (hundreds of Ω ), therefore we can approximate the output impedance as
*** QuickLaTeX cannot compile formula:
\[Z_{out} \approx R_D \label\]
*** Error message:
Emergency stop.
(2.3.3)
It should be noted that all forms of DC bias discussed in the previous chapter are game here. There are a few limitations to be aware of, though. For example, when using constant voltage bias, swamping is not possible as that bias form does not use a source resistor. In contrast, self bias and combination bias include a source resistor so swamping is a possibility, however, 𝑅𝑆 may need to be split and partially bypassed to achieve the desired results. Finally, constant current bias is not well-positioned to use swamping as that would require some additional work to fit in a new 𝑅𝑆 along with the current source. More typically, the current source will just be bypassed with a capacitor to produce a non-swamped amplifier.
Example 2.3.1
Determine the voltage gain and input impedance for the circuit shown in Figure 2.3.3 . Assume 𝐼𝐷𝑆𝑆=15 mA and 𝑉𝐺𝑆(𝑜𝑓𝑓)=−3 V.
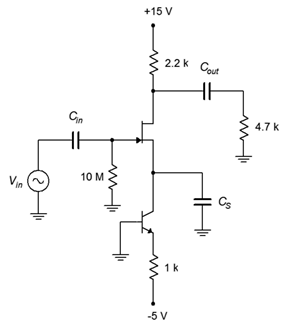
This is an unswamped common source amplifier with constant current bias. We can determine 𝑍𝑖𝑛 via inspection.
![]()
![]()
To find the voltage gain, we’ll first need to find 𝐼𝐷 and 𝑔𝑚0 in order to find 𝑔𝑚.
![]()
![]()
![]()
![]()
![]()
![]()
Knowing the current and maximum transconductance, we can find 𝑔𝑚 through the use of Equation 10.2.4.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Example 2.3.2
Determine the voltage gain and input impedance for the circuit shown in Figure 2.3.3 . Assume 𝐼𝐷𝑆𝑆=24 mA and 𝑉𝐺𝑆(𝑜𝑓𝑓)=−4 V.
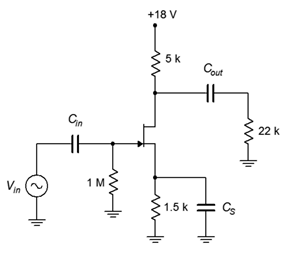
This is an unswamped common source amplifier with self bias. Once again, we can determine 𝑍𝑖𝑛 via inspection.
![]()
![]()
To find the voltage gain, we’ll first need to find 𝑔𝑚0. Also, we can take a shortcut and find the normalized drain current from the self bias graph instead of finding 𝐼𝐷 itself.
![]()
![]()
![]()
𝑅𝑆 is 1.5 kΩ, therefore 𝑔𝑚0𝑅𝑆=18. From the self bias graph this produces a normalized drain current of 0.08.
![]()
![]()
![]()
Again, there is no swamping so 𝑟𝑆=0. The gain formula reduces to
![]()
![]()
![]()
We will now turn our attention to the effect of swamping. As in the BJT case, we expect to sacrifice gain and in return, see an improvement in distortion. We shall examine this through the use of a simulation.
Computer Simulation
A common source amplifier using self bias is entered into the simulator as shown in Figure 2.3.5.
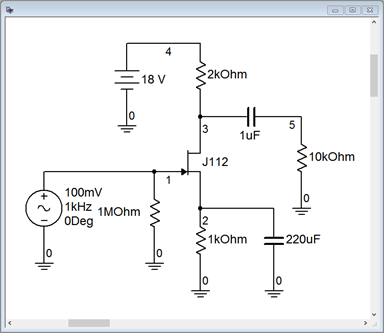
Reasonable device values for this model are 𝐼𝐷𝑆𝑆=40 mA and 𝑉𝐺𝑆(𝑜𝑓𝑓)=−2.3 V. Based on these we find
![]()
![]()
![]()
Given 𝑅𝑆=1 k Ω , the self-bias equation yields
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The results of a transient analysis are shown in Figure 2.3.6 for a 100 mV peak input signal.
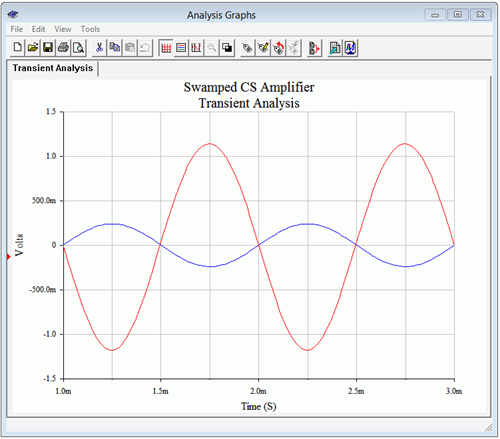
The input signal was raised to 240 mV peak in order to keep the output signals of the two versions at the same amplitude. The symmetry appears to be better here and the gain works out to −4.85, just a few percent low.
Total harmonic distortion (THD) analysis is performed next. The results are shown in Figures 2.3.8 and 2.3.9 . To keep the comparison fair, the input levels are adjusted to maintain similar output voltages. The non-swamped results are seen in Figure 2.3.8 , and as expected based on the waveform asymmetry, the THD is relatively high at roughly 4%. The swamped version scores better at just over 1.6%, although this is still not stellar performance.
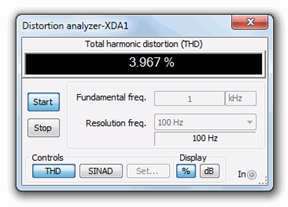
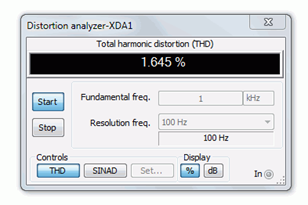
It is interesting to note that while the voltage gain of the swamped amplifier has dropped to 41% of the non-swamped gain, the THD has dropped to 41% of the nonswamped THD. In fact, given the square-law nature of the characteristic curve, we would expect the distortion to be lower if we used smaller signals. To verify this, the THD simulation is run again for the swamped amplifier, but now using an input signal ten times smaller at only 24 mV peak. The result is shown in Figure 2.3.10 .

The resulting THD is markedly lower for an order of magnitude improvement. We’re now at least approaching “hi-fi” territory.

