3.3 DE-MOSFET Biasing

As the characteristic equations of the JFET and DE-MOSFET are the same, the DC biasing model is the same. Consequently, the DE-MOSFET can be biased using any of the techniques used with the JFET including self bias, combination bias and current source bias as these are all second quadrant biasing schemes (i.e., have a negative 𝑉_𝐺𝑆 ). The self bias and combination bias equations and plots from Chapter 10 may be used without modification. The DE-MOSFET also allows first quadrant operation so a couple of new biasing forms become available: zero bias and voltage divider bias. In reality, both are variations on constant voltage bias but which utilize the first quadrant.

Zero Bias

Zero bias is unique. In some ways it can be thought of as a cross between self bias and constant voltage bias. Like self bias, it does not require a second DC source for the gate or source terminal. Like constant voltage bias, there is no need for a source resistor, 𝑅_𝑆. A prototype of zero bias is shown in Figure 3.3.1 . There is no question that it is a minimal parts-count circuit.

Zero bias is so named because it operates at 𝑉_𝐺𝑆=0 V. Recall that the gate current is ideally zero, thus there is no drop across 𝑅𝐺 and 𝑉𝐺=0 V as a consequence. The source is tied directly to ground, therefore 𝑉_𝐺𝑆 must equal 0 V. As 𝑉_𝐺𝑆 doesn’t change, this can be thought of as a form of constant voltage bias. The interesting bit is that when an AC signal is applied to the gate, its negative portion will pull the MOSFET down into depletion mode and the positive portion will push the operation into enhancement mode. Because the device can operate in this fashion, conducting current while straddling zero, so to speak, DE-MOSFETs are sometimes referred to as normally on devices.

Determining the operating point for zero bias is startlingly easy. Because 𝑉_𝐺𝑆=0 V, 𝐼_𝐷 must equal 𝐼_𝐷𝑆𝑆 and 𝑔_𝑚 must equal 𝑔_𝑚0. Like all constant voltage biasing schemes, though, Q point stability is not very good. Another point to notice is that, as there is no source resistor, this bias is only applicable to non-swamped common source amplifiers. It cannot be used with a source follower or swamped amplifier (if a small swamping resistor is inserted into the source, technically the circuit can be classified as self bias, although the AC signal may still push operation into enhancement mode).

Example 3.3.1

Determine 𝐼_𝐷 , 𝑉_𝐷 and 𝑔_𝑚0 for the circuit shown in Figure 3.3.2 . Assume 𝐼_𝐷𝑆𝑆=12 mA and 𝑉_{𝐺𝑆(𝑜𝑓𝑓)}=−3 V.

By inspection, as this is zero bias 𝐼_𝐷=𝐼_𝐷𝑆𝑆, and therefore 𝐼_𝐷=12 mA. Using KVL and Ohm’s law we can find 𝑉_𝐷.

   

   

   

   

   

   

Voltage Divider Bias

Voltage divider bias is a form of constant voltage bias that operates in enhancement mode. A prototype circuit is shown in Figure 3.3.3 . Note that the source terminal is connected directly to ground. This is important. If this was not the case, this would be a form of combination bias (basically shifting the 𝑉_𝑆𝑆 supply up to ground and then shifting the gate voltage from ground up to a positive 𝑉_𝑆𝑆 to maintain the same differential voltage). As such, it would be operating in depletion mode.

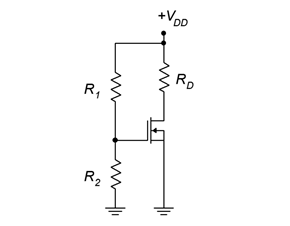
The voltage divider comprised of 𝑅₁ and 𝑅₂ will establish a DC bias potential on the gate. As the source is at ground, 𝑉_𝐺𝑆=𝑉_𝐺=𝑉_𝑅2. Given that 𝑉_𝐷𝐷 must be positive, then 𝑉_𝐺𝑆 must be positive, and enhancement mode operation is a given.

The most direct way to handle this is to determine the voltage divider potential and use either the characteristic equation (Equation 10.2.1) or associated graph to determine the drain current. Once 𝐼_𝐷 is found, the drain-source voltage may be found via the standard Ohm’s law/KVL route.

Before continuing, note that the values of the divider resistors can be very high without creating biasing problems (unlike the BJT version of voltage divider bias). This is because the gate current is so small that even when using megohm values for the divider, the loading caused by the gate will not be noticeable.

Example 3.3.2

For the circuit of Figure 3.3.4 , determine 𝐼_𝐷 and 𝑉_𝐷. Assume 𝐼_𝐷𝑆𝑆=2 mA and 𝑉_𝐺𝑆(𝑜𝑓𝑓)=−6 V.

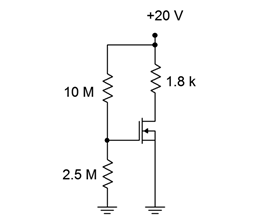
The voltage divider will yield 𝑉_𝐺𝑆.

   

   

   

Use Equation 10.2.1 to find 𝐼_𝐷 .

   

   

   

Use KVL and Ohm’s law to find 𝑉_𝐷.

   

   

   

Alternately, using the curve of Figure 3.2.3, we would first find the normalized gate-source voltage which is 4 V/6 V or 0.667 (note that the curve plots −𝑉_𝐺𝑆/𝑉_{𝐺𝑆(𝑜𝑓𝑓)} so that the quadrants do not appear reversed). From this the normalized drain current, 𝐼_𝐷/𝐼_𝐷𝑆𝑆, may be determined to be approximately 2.8, yielding a drain current of 5.6 mA.