2.4 Common Drain Amplifier

James Fiore

2.4 Common Drain Amplifier

The common drain amplifier is analogous to the common collector emitter follower. The JFET version is also known as a source follower. The prototype amplifier circuit with device model is shown in Figure 2.4.1 . As with all voltage followers, we expect a non-inverting voltage gain close to unity, a high 𝑍_𝑖𝑛 and low 𝑍_𝑜𝑢𝑡.

Figure 2.4.1: Common drain (source follower) prototype.

The input signal is presented to the gate terminal while the output is taken from the source. Many bias circuits may be used here as long as they do not have a grounded source terminal such as constant voltage bias.

Voltage Gain

In order to develop an equation for the voltage gain, 𝐴_𝑣, we follow the same path we took with the common source amplifier earlier in this chapter. First, we start with the fundamental definition, namely that voltage gain is the ratio of 𝑣_𝑜𝑢𝑡 to 𝑣_𝑖𝑛, and proceed by expressing these voltages in terms of their Ohm’s law equivalents.

$A_v = \frac{g_m r_L}{g_m r_L+1}$

(2.4.1)

Equation 2.4.1 is very similar to the gain equation derived for the swamped common source amplifier; the notable changes being the lack of the minus sign indicating that this circuit does not invert the signal, and 𝑟_𝐿 replacing 𝑟_𝑆 in the denominator. It is worth remembering that 𝑟_𝐿 here is the AC source resistance while in the common source amplifier 𝑟_𝐿 is the AC drain resistance. To avoid potential confusion, this equation could also be written as

$A_v = \frac{g_m r_S}{g_m r_S+1}$

(2.4.2)

In any event, the goal is to make sure that 𝑔_𝑚𝑟_𝑆≫1 . By doing so, the voltage gain will be very close to unity.

Input Impedance

The analysis for common drain input impedance is virtually identical to that for the swamped common source amplifier. The result is replicated here for convenience.

$Z_{in} = r_G || r_{GS} \approx r_G$

(2.4.3)

Output Impedance

In order to investigate the output impedance, we’ll separate the load resistance from the source bias resistor, as shown in Figure 2.4.2.

From the position of 𝑅_𝐿, looking back toward the source we find 𝑅_𝑆 in parallel with the impedance looking back into the source terminal. The voltage at this node is 𝑣_𝐺𝑆 and the current entering this node is 𝑖_𝐷. The ratio of the two must yield the impedance looking into the source.

$Z_{source} = \frac{v_{GS}}{i_D}$

$Z_{source} = \frac{v_{GS}}{g_m v_{GS}}$

$Z_{source} = \frac{1}{g_m}$

(2.4.4)

Therefore, the output impedance is

$Z_{out} = R_S || \frac{1}{g_m}$

(2.4.5)

We can expect this value to be much smaller than the output impedance of typical common source amplifiers.

Example 2.4.1

For the follower shown in Figure 2.4.3 , determine the input impedance and output voltage. Assume 𝑉_𝑖𝑛=100 mV, 𝐼_𝐷𝑆𝑆=30 mA, 𝑉_{𝐺𝑆(𝑜𝑓𝑓)}=−2 V.

This is a follower using self bias. We’ll find 𝑔_𝑚 via the self bias graph.

$g_{m0} =- \frac{2 I_{DSS}}{V_{GS (off )}}$

$g_{m0} =- \frac{60 mA}{-2 V}$

$g_{m0} = 30 mS$

𝑅_𝑆 is 1 k Ω , yielding 30 for 𝑔_𝑚0𝑅_𝑆 . The normalized drain current from the self bias graph is approximately 0.05.

$g_m = g_{m0} \sqrt{\frac{I_D}{I_{DSS}}}$

$g_m = 30mS\sqrt{0.05}$

$g_m = 6.71 mS$

$A_v = \frac{g_m r_S}{g_m r_S+1}$

$A_v = \frac{6.71mS(1 k\Omega || 600 \Omega)}{6.71 mS(1k \Omega || 600\Omega)+1}$

$A_v = 0.716$

Thus 𝑉_𝑜𝑢𝑡 is 71.6 mV. By inspection, 𝑍_𝑖𝑛 may be approximated as 2.2 M Ω .

Example 2.4.2

For the circuit shown in Figure 2.4.4 , determine the input impedance and output voltage. Assume 𝑉_𝑖𝑛=100 mV, 𝐼_𝐷𝑆𝑆=36 mA, 𝑉_{𝐺𝑆(𝑜𝑓𝑓)}=3 V.

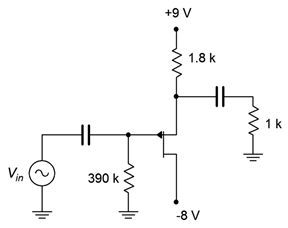
This follower uses combination bias with a P-channel JFET. Note that the source is at the top. We’ll find 𝑔_𝑚 via the combination bias graph for 𝑘=3 ( 𝑘=𝑉_𝑆𝑆/_{𝑉𝐺𝑆(𝑜𝑓𝑓)}) .

$g_{m0} = \frac{2 I_{DSS}}{V_{GS( off )}}$