The Decibel
Most people are familiar with the term “decibel” in reference to sound pressure. It’s not uncommon to hear someone say something such as “It was 110 decibels at the concert last night, and my ears are still ringing.” This popular use is somewhat inaccurate, but does show that decibels indicate some sort of quantity — in this case, sound pressure level.
Decibel Representation of Power and Voltage Gains
In its simplest form, the decibel is used to measure some sort of gain, such as power or voltage gain. Unlike the ordinary gain measurements that you may be familiar with, the decibel form is logarithmic. Because of this, it can be very useful for showing ratios of change, as well as absolute change. The base unit is the Bel. To convert an ordinary gain to its Bel counterpart, just take the common log (base 10) of the gain. In equation form:
![]()
Note that on most hand calculators common log is denoted as “log” while the natural log is given as “ln”. Unfortunately, some programming languages use “log” to indicate natural log and “log10” for common log. More than one student has been bitten by this bug, so be forewarned! As an example, if a circuit produces an output power of 200 milliwatts for an input of 10 milliwatts, we would normally say that it has a power gain of:
![]()
![]()
![]()
For the Bel version, just take the log of this result.
![]()
![]()
![]()
The Bel gain is 1.3 Bels. The term “Bels” is not a unit in the strict sense of the word (as in “watts”), but is simply used to indicate that this is not an ordinary gain. In contrast, ordinary power and voltage gains are sometimes given units of W/W and V/V to distinguish them from Bel gains. Also, note that the symbol for Bel power gain is G’ and not G. All Bel gains are denoted with the following prime (’) notation to avoid confusion. Because Bels tend to be rather large, we typically use one-tenth of a Bel as the norm. The result is the decibel (one-tenth Bel). To convert to decibels, simply multiply the number of Bels by 10. Our gain of 1.3 Bels is equivalent to 13 decibels. The units are commonly shortened to dB. Consequently, we may say:
![]()
(7.2.1)
Where the result is in dB.
At this point, you may be wondering what the big advantage of the decibel system is. To answer this, recall a few log identities. Normal multiplication becomes addition in the log system, and division becomes subtraction. Likewise, powers and roots become multiplication and division. Because of this, two important things show up. First, ratios of change become constant offsets in the decibel system, and second, the entire range of values diminishes in size. The result is that a very wide range of gains may be represented within a fairly small scope of values, and the corresponding calculations can become quicker. There are a couple of dB values that are useful to remember. With the aid of your hand calculator, it is very easy to show the following:
| Factor | dB Value using 𝐺′=10 log 10𝐺 |
|---|---|
| 1 | 0 dB |
| 2 | 3.01 dB |
| 4 | 6.02 dB |
| 8 | 9.03 dB |
| 10 | 10 dB |
Table 7.2.1
We can also look at fractional factors (i.e., losses instead of gains.)
| Factor | dB Value |
|---|---|
| 0.5 | −3.01 dB |
| 0.25 | −6.02 dB |
| 0.125 | −9.03 dB |
| 0.1 | −10 dB |
Table 7.2.2
If you look carefully, you will notice that a doubling is represented by an increase of approximately 3 dB. A factor of 4 is in essence, two doublings. Therefore, it is equivalent to 3 dB + 3 dB, or 6 dB. Remember, because we are using logs, multiplication turns into simple addition. In a similar manner, a halving is represented by approximately −3 dB. The negative sign indicates a reduction. To simplify things a bit, think of factors of 2 as ±3 dB, the sign indicating whether you are increasing (multiplying), or decreasing (dividing). As you can see, factors of 10 work out to a very convenient 10 dB. By remembering these two factors, you can often estimate a dB conversion without the use of your calculator. For instance, we could rework our initial conversion problem as follows:
- The amplifier has a gain of 20
- 20 can be written as 2 times 10
- The factor of 2 is 3 dB, the factor of 10 is 10 dB
- The answer must be 3 dB + 10 dB, or 13 dB
- This verifies our earlier result
Time for a few examples.
Example 7.2.1
An amplifier has a power gain of 800. What is the decibel power gain?
![]()
![]()
![]()
We could also use our estimation technique:
- G = 800 = 8∙102
- 8 is equivalent to 3 factors of 2, or 2∙2∙2, and can be expressed as 3 dB + 3 dB + 3 dB, which is, of course, 9 dB
- 102 is equivalent to 2 factors of 10, or 10 dB + 10 dB = 20 dB
- The result is 9 dB + 20 dB, or 29 dB
Note that if the leading digit is not a power of 2, the estimation will not be as precise. For example, if the gain is 850, you know that the decibel gain is just a bit over 29 dB. You also know that it must be less than 30 dB (1000=103 which is 3 factors of 10, or 30 dB.) As you can see, by using the dB form, you tend to concentrate on the magnitude of gain, and not so much on trailing digits.
Example 7.2.2
An attenuator reduces signal power by a factor of 10,000. What is this loss expressed in dB?
![]()
![]()
By using the approximation, we can say,
![]()
The negative exponent tells us we have a loss (negative dB value), and 4 factors of 10.
![]()
![]()
Remember, if an increase in signal is produced, the result will be a positive dB value. A decrease in signal will always result in a negative dB value. A signal that is unchanged indicates a gain of unity, or 0 dB.
To convert from dB to ordinary form, just invert the steps; that is, divide by ten and then take the antilog.
![]()
On most hand calculators, base 10 antilog is denoted as 10x. In most computer languages, you just raise 10 to the appropriate power, as in G = 10.0^(Gprime / 10.0) (BASIC), or use an exponent function, as in pow(10.0, Gprime / 10.0) (C or Python).
Example 7.2.3
An amplifier has a power gain of 23 dB. If the input is 1 mW, what is the output?
In order find the output power, we need to find the ordinary power gain, G.
![]()
![]()
![]()
Therefore, Pout =199.5 ∙ 1 mW, or 199.5 mW
You could also use the approximation technique in reverse. To do this, break up the dB gain in 10 dB and 3 dB chunks:
![]()
Now replace each chunk with the appropriate factor, and multiply them together (remember, when going from log to ordinary form, addition turns into multiplication.)
![]()
![]()
While the approximation technique appears to be slower than the calculator, practice will show otherwise. Being able to quickly estimate dB values can prove to be a very handy skill in the electronics field. This is particularly true in larger, multi-stage designs.
Example 7.2.4
A three-stage amplifier has gains of 10 dB, 16 dB, and 14 dB per section. What is the total dB gain?
Because dB gains are a log form, just add the individual stage gains to arrive at the system gain.
![]()
![]()
![]()
As you may have noticed, all of the examples up to this point have used power gain and not voltage gain. You may be tempted to use the same equations for voltage gain. In a word, don’t. If you think back for a moment, you will recall that power varies as the square of voltage. In other words, a doubling of voltage will produce a quadrupling of power. If you were to use the same dB conversions, a doubling of voltage would be 3 dB, yet, because the power has quadrupled, this would indicate a 6 dB rise. Consequently, voltage gain (and current gain as well) are treated in a slightly different fashion. We would rather have our doubling of voltage work out to 6 dB, so that it matches the power calculation. The correction factor is very simple. Because power varies as the second power of voltage, the dB form should be twice as large for voltage (remember, exponentiation turns into multiplication when using logs). Applying this factor to equation 1.1 yields:
![]()
(7.2.2
Be careful though, the Bel voltage gain only equals the Bel power gain if the input and output impedances of the system are matched (you may recall from your earlier work that it is quite possible to design a circuit with vastly different voltage and power gains. A voltage follower, for example, exhibits moderate power gain with a voltage gain of unity. It is quite likely that the follower will not exhibit matched impedances.) If we were to recalculate our earlier table of common factors, we would find that a doubling of voltage gain is equivalent to a 6 dB rise, and a ten fold increase is equivalent to a 20 dB rise, twice the size of their power gain counterparts.
Note that current gain may be treated in the same manner as voltage gain (although this is less commonly done in practice).
Example 7.2.5
An amplifier has an output signal of 2 V for an input of 50 mV. What is A’v? First find the ordinary gain.
![]()
Now convert to dB form.
![]()
![]()
![]()
The approximation technique yields 40 = 2∙2∙10, or 6 dB + 6 dB + 20 dB = 32 dB
To convert A’v to A, reverse the process.
![]()
Example 7.2.6
An amplifier has a gain of 26 dB. If the input signal is 10 mV, what is the output?
![]()
![]()
![]()
![]()
![]()
The final point to note in this section is that, as in the case of power gain, a negative dB value indicates a loss. Therefore, a 2:1 voltage divider would have a gain of −6 dB.
Signal Representation in dBW and dBV
As you can see from the preceding section, it is possible to spend considerable time converting between decibel gains and ordinary voltages and powers. Because the decibel form does offer advantages for gain measurement, it would make sense to use a decibel form for power and voltage levels as well. This is a relatively straightforward process. There is no reason why we can’t express a power or voltage in a logarithmic form. Because a dB value just indicates a ratio, all we need to do is decide on a reference (i.e., a comparative base for the ratio). For power measurements, a likely choice would be 1 watt. In other words, we can describe a power as being a certain number of dB above or below 1 watt. Positive values will indicate powers greater than 1 watt, while negative values will indicate powers less than 1 watt. In general equation form:
![]()
(7.2.3)
The answer will have units of dBW, that is, decibels relative to 1 watt.
Example 7.2.7
A power amplifier has a maximum output of 120 W. What is this power in dBW?
![]()
![]()
![]()
There is nothing sacred about the 1 watt reference, short of its convenience. We could just as easily choose a different reference. Other common reference points are 1 milliwatt (dBm) and 1 femtowatt (dBf). Obviously, dBf is used for very low signal levels, such as those coming from an antenna. dBm is in very wide use in the communications industry. To use these other references, just divide the given power by the new reference.
Example 7.2.8
A small personal music player delivers 200 mW to its headphones. What is this output power in dBW, and in dBm?
For an answer in units of dBW, use the 1 watt reference
![]()
![]()
![]()
For units of dBm, use a 1 milliwatt reference
![]()
![]()
![]()
200 mW, −7 dBW, and 23 dBm are three ways of saying the same thing. Note that the dBW and dBm values are 30 dB apart. This will always be true, because the references are a factor of 1000 (30 dB) apart.
In order to transfer a dBW or similar value into watts, reverse the process.
![]()
Example 7.2.9
A studio microphone produces a 12 dBm signal while recording normal speech. What is the output power in watts?
![]()
![]()
![]()
For voltages, we can use a similar system. A logical reference is 1 V, with the resulting units being dBV. As before, these voltage measurements will use a multiplier of 20 instead of 10.
![]()
(7.2.4)
Example 7.2.10
A test oscillator produces a 2 V signal. What is this value in dBV?
![]()
![]()
![]()
When both circuit gains and signal levels are specified in dB form, analysis can be very quick. Given an input level, simply add the gain to it in order to find the output level. Given input and output levels, subtract them in order to find the gain.
Example 7.2.11
A computer hard drive read/write amplifier exhibits a gain of 35 dB. If the input signal is −42 dBV, what is the output signal?
![]()
![]()
![]()
Note that the final units are dBV and not dB, thus indicating a voltage and not merely a gain.
Example 7.2.12
A guitar power amp needs an input of 20 dBm to achieve an output of 25 dBW. What is the gain of the amplifier in dB?
First, it is necessary to convert the power readings so that they share the same reference unit. Because dBm represents a reference 30 dB smaller than the dBW reference, just subtract 30 dB to compensate.
![]()
![]()
![]()
![]()
Note that the units are dB and not dBW. This is very important! Saying that the gain is “so many” dBW is the same as saying the gain is “so many” watts. Obviously, gains are “pure” numbers and do not carry units such as watts or volts.
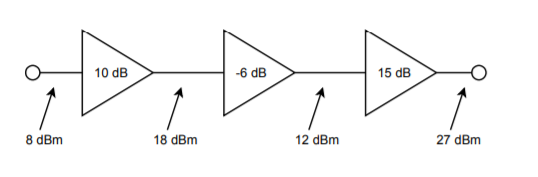
The usage of a dB-based system is shown graphically in Figure 1.1. Note how the stage gains are added to the input signal to form the output. Even large circuits can be quickly analyzed in this form. To make life in the lab even easier, it is possible to take measurements directly in dB form. By doing this, you need never convert while troubleshooting a design. For general-purpose work, voltage measurements are the norm, and therefore a dBV scale is often used.
Items Of Interest In The Laboratory
When using a digital meter on a dBV scale it is possible to “underflow” the meter if the signal is too weak. This will happen if you try to measure around zero volts, for example. If you attempt to calculate the corresponding dBV value, your calculator will probably show “error”. The effective value is negative infinite dBV. The meter will certainly have a hard time showing this value! Another item of interest revolves around the use of dBm measurements. It is common to use a voltmeter to make dBm measurements, in lieu of a wattmeter. While the connections are considerably simpler, a voltmeter cannot measure power. How is this accomplished then? Well, as long as the circuit impedance is known, power can be derived from a voltage measurement. A common impedance in communication systems (such as recording studios) is 600 Ω, so a meter can be calibrated to give correct dBm readings by using Power Law. If this meter is used on a non-600 Ω circuit, the readings will no longer reflect accurate dBm values (but will still properly reflect relative changes in dB).

