2.8 Exercises

Analysis Problems

  1. For the amplifier of Figure 11.8.1 , determine 𝑍𝑖𝑛 and 𝐴𝑣. 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝑉𝐷𝐷 = 15 V, 𝑅𝐺 = 220 k Ξ© , 𝑅𝐷 = 2 k Ξ© , 𝑅𝐿 = 3.3 k Ξ© , 𝑅𝑆 = 330 Ξ©.
  2. For the amplifier of Figure 11.8.1 , determine 𝑍𝑖𝑛 and π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛 = 50 mV, 𝐼𝐷𝑆𝑆 = 15 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝑉𝐷𝐷 = 20 V, 𝑅𝐺 = 270 k Ξ© , 𝑅𝐷 = 2 k Ξ© , 𝑅𝐿 = 6.8 k Ξ© , 𝑅𝑆 = 270 Ξ©.
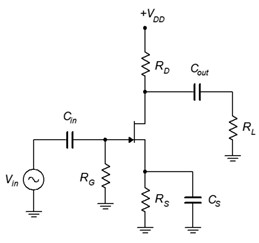
    Figure 2.8.1
  3. For the amplifier of Figure 11.8.2 , determine 𝑍𝑖𝑛 and π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛= 60 mV, 𝐼𝐷𝑆𝑆 = 10 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝑉𝐷𝐷 = 20 V, 𝑉𝑆𝑆 = βˆ’6 V, 𝑅𝐺 = 270 k Ξ© , 𝑅𝐷 = 2 k Ξ© , 𝑅𝐿 = 4 k Ξ© , 𝑅𝑆 = 1.8 k Ξ© , π‘…π‘†π‘Š = 200 Ξ© .
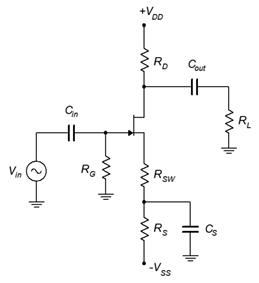
    Figure 2.8.2
  4. For the amplifier of Figure 11.8.2 , determine 𝑍𝑖𝑛 and 𝐴𝑣. 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝑉𝐷𝐷 = 18 V, 𝑉𝑆𝑆 = βˆ’4 V, 𝑅𝐺 = 330 k Ξ© , 𝑅𝐷 = 2.2 k Ξ© , 𝑅𝐿 = 10 k Ξ© , 𝑅𝑆 = 3 k Ξ© , π‘…π‘†π‘Š = 100 Ξ© .
  5. For the amplifier of Figure 11.8.3 , determine 𝑍𝑖𝑛 and 𝐴𝑣. 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝑉𝐷𝐷 = 18 V, 𝑉𝐸𝐸 = βˆ’4 V, 𝑅𝐺 = 390 k Ξ© , 𝑅𝐷 = 2.2 k Ξ© , 𝑅𝐸 = 1 k Ξ© , 𝑅𝐿 = 20 k Ξ©.
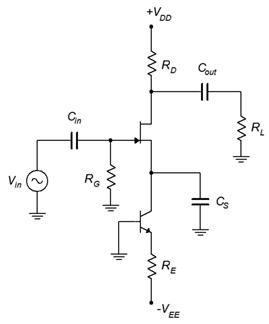
    Figure 2.8.3
  6. For the amplifier of Figure 11.8.3 , determine 𝑍𝑖𝑛 and π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛 = 70 mV, 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝑉𝐷𝐷 = 18 V, 𝑉𝐸𝐸 = βˆ’4 V, 𝑅𝐺 = 390 k Ξ© , 𝑅𝐷 = 2.2 k Ξ© , 𝑅𝐿 = 20 k Ξ©.
  7. For the circuit of Figure 11.8.4 , determine 𝑍𝑖𝑛 and 𝐴𝑣. 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝑉𝐷𝐷 = 10 V, 𝑅𝐺 = 220 k Ξ© , 𝑅𝐿 = 3.3 k Ξ© , 𝑅𝑆 = 330 Ξ© .
    Figure 2.8.4
  8. For the circuit of Figure 11.8.4 , determine 𝑍𝑖𝑛 and π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛 = 200 mV, 𝐼𝐷𝑆𝑆 = 15 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝑉𝐷𝐷 = 12 V, 𝑅𝐺 = 270 k Ξ© , 𝑅𝐿 = 1.8 k Ξ© , 𝑅𝑆 = 270 Ξ© .
  9. For the circuit of Figure 11.8.5 , determine 𝑍𝑖𝑛 and π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛 = 100 mV, 𝐼𝐷𝑆𝑆 = 10 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝑉𝐷𝐷 = 15 V, 𝑉𝑆𝑆 = βˆ’6 V, 𝑅𝐺 = 470 k Ξ© , 𝑅𝐿 = 4 k Ξ© , 𝑅𝑆 = 1.8 k Ξ©.
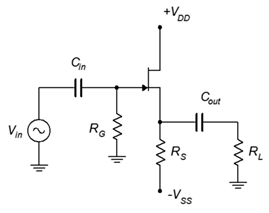
    Figure 2.8.5
  10. For the circuit of Figure 11.8.5 , determine 𝑍𝑖𝑛 and 𝐴𝑣. 𝐼𝐷𝑆𝑆 = 18 mA, 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝑉𝐷𝐷 = 14 V, 𝑉𝑆𝑆 = βˆ’6 V, 𝑅𝐺 = 360 k Ξ© , 𝑅𝐿 = 10 k Ξ© , 𝑅𝑆 = 1 k Ξ© .
  11. For the circuit of Figure 11.8.6 , determine π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛 = 100 mV, π‘Ÿπ·π‘†(π‘œπ‘›) = 50 Ξ© , π‘Ÿπ·π‘†(π‘œπ‘“π‘“) = 1 M Ξ© , 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝑉𝐢 = βˆ’6 V, 𝑅𝐺 = 270 k Ξ© , 𝑅𝐷 = 6.8 k Ξ© .
  12. For the circuit of Figure 11.8.6, determine π‘‰π‘œπ‘’π‘‘. 𝑉𝑖𝑛 = 100 mV, π‘Ÿπ·π‘†(π‘œπ‘›) = 75 Ξ© , π‘Ÿπ·π‘†(π‘œπ‘“π‘“) = 750 k Ξ© , 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝑉𝐢 = 0 V, 𝑅𝐺 = 180 k Ξ© , 𝑅𝐷 = 5.1 k Ξ© .
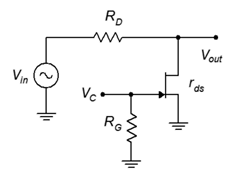
    Figure 2.8.6

Design Challenge Problems

  1. Following the circuit of Figure 11.8.2 , design an amplifier with a gain of at least 4 and an input impedance of at least 300 k Ξ©. 𝑅𝐿 = 10 k Ξ© . The JFET has the following parameters: 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝐼𝐷𝑆𝑆 = 15 mA. Try to use standard resistor values.
  2. Using the circuit of Figure 11.8.4 , design a follower with a gain of at least 0.7 and an input impedance of at least 500 k Ξ©. 𝑅𝐿 = 1 k Ξ© . The JFET has the following parameters: 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝐼𝐷𝑆𝑆 = 20 mA. Try to use standard resistor values.

Computer Simulation Problems

  1. Utili 𝑍𝑖𝑛 g manufacturer’s data sheets, find devices with the following specifications (typical) and verify them using the measurement techniques presented in the prior chapter. Device 1: 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’2 V, 𝐼𝐷𝑆𝑆 = 15 mA. Device 2: 𝑉𝐺𝑆(π‘œπ‘“π‘“) = βˆ’3 V, 𝐼𝐷𝑆𝑆 = 20 mA.
  2. Using the device model from the preceding problem, verify the design of Problem 13.
  3. Using the device model from Problem 15, verify the design of Problem 14.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Avionics II Copyright © 2023 by NSCC is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book