3.8 Exercises
Analysis Problems
- For the circuit of Figure 3.8.1 , determine 𝐼𝐷, 𝑉𝐺 and 𝑉𝐷. 𝐼𝐷𝑆𝑆 = 20 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −6 V, 𝑉𝐷𝐷 = 15 V, 𝑅𝐺 = 470 k Ω , 𝑅𝑆 = 1.2 k Ω , 𝑅𝐷 = 1.8 k Ω .
- For the circuit of Figure 3.8.1 , determine 𝐼𝐷, 𝑉𝐷𝑆 and 𝑉𝐷. 𝐼𝐷𝑆𝑆 = 20 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −5 V, 𝑉𝐷𝐷 = 30 V, 𝑅𝐺 = 560 k Ω , 𝑅𝑆 = 420 Ω , 𝑅𝐷 = 1.5 k Ω .
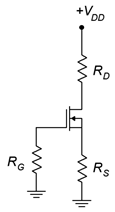
Figure 3.8.1 - For Figure 3.8.2 , determine 𝐼𝐷 , 𝑉𝐺 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 15 mA, 𝑉𝐷𝐷 = 25 V, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −3 V, 𝑉𝑆𝑆 = −6 V, 𝑅𝐺 = 820 k Ω , 𝑅𝑆 = 2 k Ω , 𝑅𝐷 = 3.6 k Ω .
- For the circuit of Figure 3.8.2 , determine 𝐼𝐷 , 𝑉𝐷𝑆 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 18 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −3 V, 𝑉𝐷𝐷 = 30 V, 𝑉𝑆𝑆 = −9 V, 𝑅𝐺 = 910 k Ω , 𝑅𝑆 = 1.2 k Ω , 𝑅𝐷 = 2.7 k Ω .
- For the circuit of Figure 3.8.3 , determine 𝐼𝐷 , 𝑉𝐺 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −4 V, 𝑉𝐷𝐷 = 35 V, 𝑅𝐺 = 680 k Ω , 𝑅𝐷 = 1.8 k Ω .

Figure 3.8.2 - For the circuit of Figure 3.8.3 , determine 𝐼𝐷 , 𝑉𝐷𝑆 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 8 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −2 V, 𝑉𝐷𝐷 = 30 V, 𝑅𝐺 = 750 k Ω , 𝑅𝐷 = 2.7 k Ω .
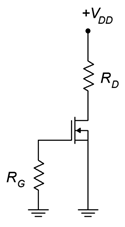
Figure 3.8.3 - For the circuit of Figure 3.8.4 , determine 𝐼𝐷 , 𝑉𝐺 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 8 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −4 V, 𝑉𝐷𝐷 = 30 V, 𝑅1 = 2.7 M Ω , 𝑅2 = 110 k Ω , 𝑅𝐷 = 470 Ω .
- For the circuit of Figure 3.8.4 , determine 𝐼𝐷 , 𝑉𝐷𝑆 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −6 V, 𝑉𝐷𝐷 = 20 V, 𝑅1 = 2 M Ω , 𝑅2 = 100 k Ω , 𝑅𝐷 = 680 Ω .
- For the circuit of Figure 3.8.5 , determine 𝐼𝐷 , 𝑉𝐺 and 𝑉𝐷 . 𝐼𝐷(𝑜𝑛) = 8 mA, 𝑉𝐺𝑆(𝑜𝑛) = 5 V, 𝑉𝐺𝑆(𝑡ℎ) = 3 V, 𝑉𝐷𝐷 = 30 V, 𝑅1 = 2 M Ω , 𝑅2 = 330 k Ω , 𝑅𝐷 = 1.2 k Ω .
- For the circuit of Figure 3.8.5 , determine 𝐼𝐷 , 𝑉𝐷𝑆 and 𝑉𝐷 . 𝐼𝐷(𝑜𝑛) = 12 mA, 𝑉𝐺𝑆(𝑜𝑛) = 6 V, 𝑉𝐺𝑆(𝑡ℎ) = 2.5 V, 𝑉𝐷𝐷 = 25 V, 𝑅1 = 1.5 M Ω , 𝑅2 = 470 k Ω , 𝑅𝐷 = 680 Ω .
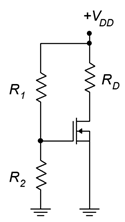
Figure 3.8.4 
Figure 3.8.5 - For the circuit of Figure 3.8.6 , determine 𝐼𝐷 , 𝑉𝐺 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 12 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 2 V, 𝑉𝐷𝐷 = −25 V, 𝑅𝐺 = 470 k Ω , 𝑅𝑆 = 800 Ω , 𝑅𝐷 = 1.8 k Ω .
- For the circuit of Figure 3.8.6 , determine 𝐼𝐷 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 10 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 2 V, 𝑉𝐷𝐷 = −20 V, 𝑅𝐺 = 560 k Ω , 𝑅𝑆 = 680 Ω , 𝑅𝐷 = 1.5 k Ω .
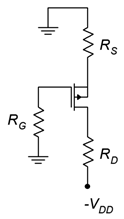
Figure 3.8.6 - For the circuit of Figure 3.8.7 , determine 𝐼𝐷, 𝑉𝐺 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 14 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 3 V, 𝑉𝐷𝐷 = −25 V, 𝑉𝑆𝑆 = 6 V, 𝑅𝐺 = 780 k Ω , 𝑅𝑆 = 2 k Ω , 𝑅𝐷 = 3.3 k Ω .

Figure 3.8.7 - For the circuit of Figure 3.8.7 , determine 𝐼𝐷 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 16 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 3.5 V, 𝑉𝐷𝐷 = −20 V, 𝑉𝑆𝑆 = 7 V, 𝑅𝐺 = 1 M Ω , 𝑅𝑆 = 1.5 k Ω , 𝑅𝐷 = 2.2 k Ω .
- For the circuit of Figure 3.8.8 , determine 𝐼𝐷 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 11 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 2 V, 𝑉𝐷𝐷 = −24 V, 𝑅𝐺 = 750 k Ω , 𝑅𝐷 = 1.2 k Ω .
- For the circuit of Figure 3.8.8 , determine 𝐼𝐷 and 𝑉𝐷 . 𝐼𝐷𝑆𝑆 = 9 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 3 V, 𝑉𝐷𝐷 = −18 V, 𝑅𝐺 = 430 k Ω , 𝑅𝐷 = 910 Ω .

Figure 3.8.8
Design Problems
- Using the circuit of Figure 3.8.1 , determine a value for 𝑅𝑆 to set 𝐼𝐷 to 4 mA. 𝐼𝐷𝑆𝑆 = 10 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −2 V, 𝑉𝐷𝐷 = 18 V, 𝑅𝐺 = 470 k Ω , 𝑅𝐷 = 1.5 k Ω .
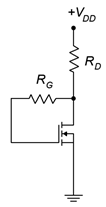
Figure 3.8.9 - For the circuit of Figure 3.8.9 , determine 𝑅𝐷 and 𝑅𝐺 to set 𝐼𝐷 = 10 mA. 𝐼𝐷(𝑜𝑛) = 15 mA, 𝑉𝐺𝑆(𝑜𝑛) = 6 V, 𝑉𝐺𝑆(𝑡ℎ) = 2 V, 𝑉𝐷𝐷 = 20 V.
- For the circuit of Figure 3.8.9 , determine 𝑅𝐷 and 𝑅𝐺 to set 𝐼𝐷 = 15 mA. 𝐼𝐷(𝑜𝑛) = 10 mA, 𝑉𝐺𝑆(𝑜𝑛) = 5 V, 𝑉𝐺𝑆(𝑡ℎ) = 2 V, 𝑉𝐷𝐷 = 25 V.
Challenge Problems
- Using the circuit of Figure 3.8.2 , determine values for 𝑅𝐷 , 𝑅𝑆 and 𝑉𝑆𝑆 to set 𝐼𝐷 to 5 mA and 𝑉𝐷 to 20 V. 𝐼𝐷𝑆𝑆 = 15 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = −3 V, 𝑉𝐷𝐷 = 30 V, 𝑅𝐺 = 560 k Ω .
- Using the circuit of Figure 3.8.10 , determine values for 𝑅𝐷 to set 𝑉𝐷 to 15 V. 𝐼𝐷𝑆𝑆 = 10 mA, 𝑉𝐺𝑆(𝑜𝑓𝑓) = 3 V, 𝑉𝑆𝑆 = 25 V, 𝑅𝐺 = 680 k Ω .
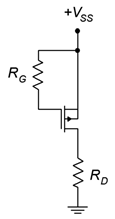
Figure 3.8.10 
Figure 3.8.11 : Comic from xkcd.com

